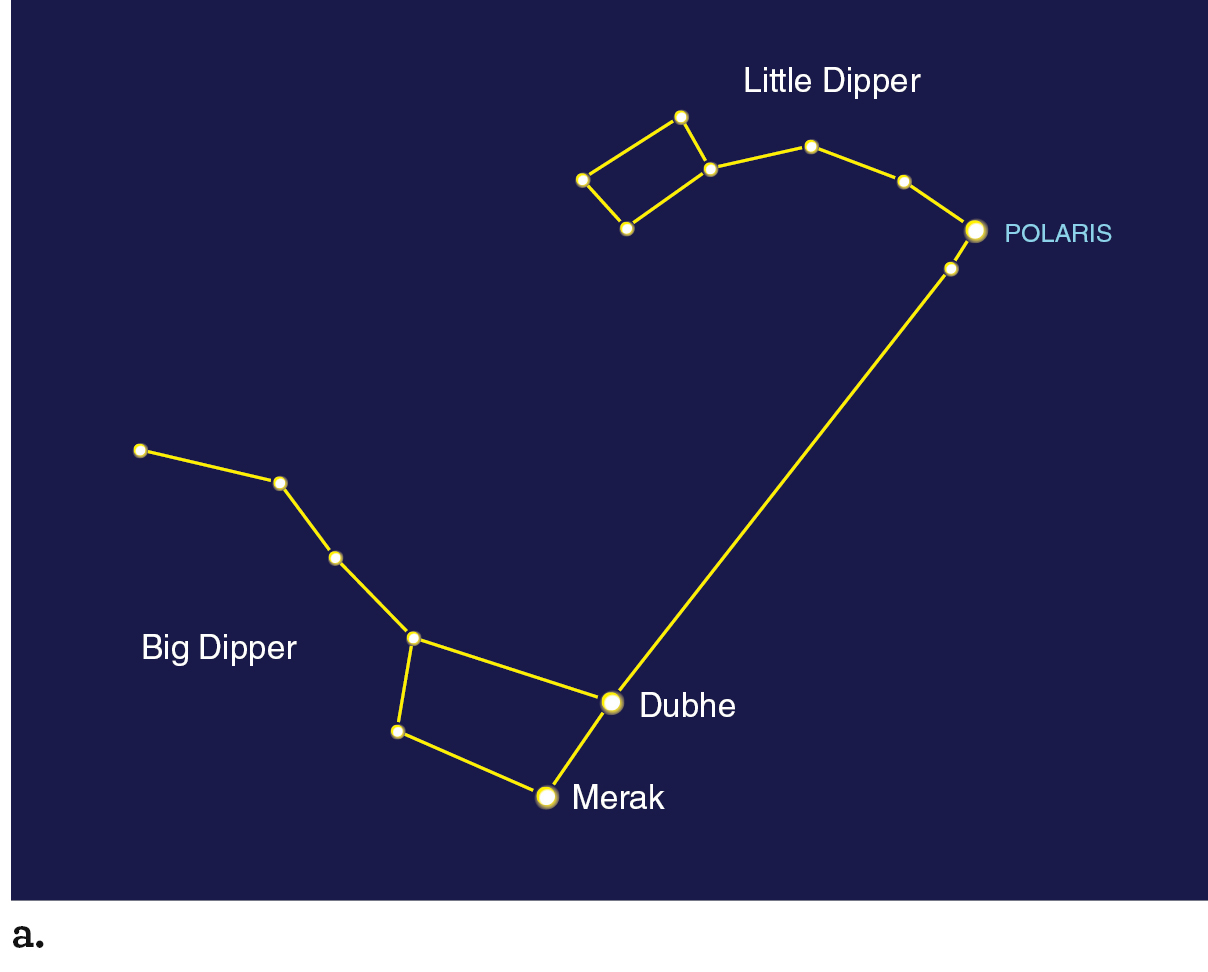
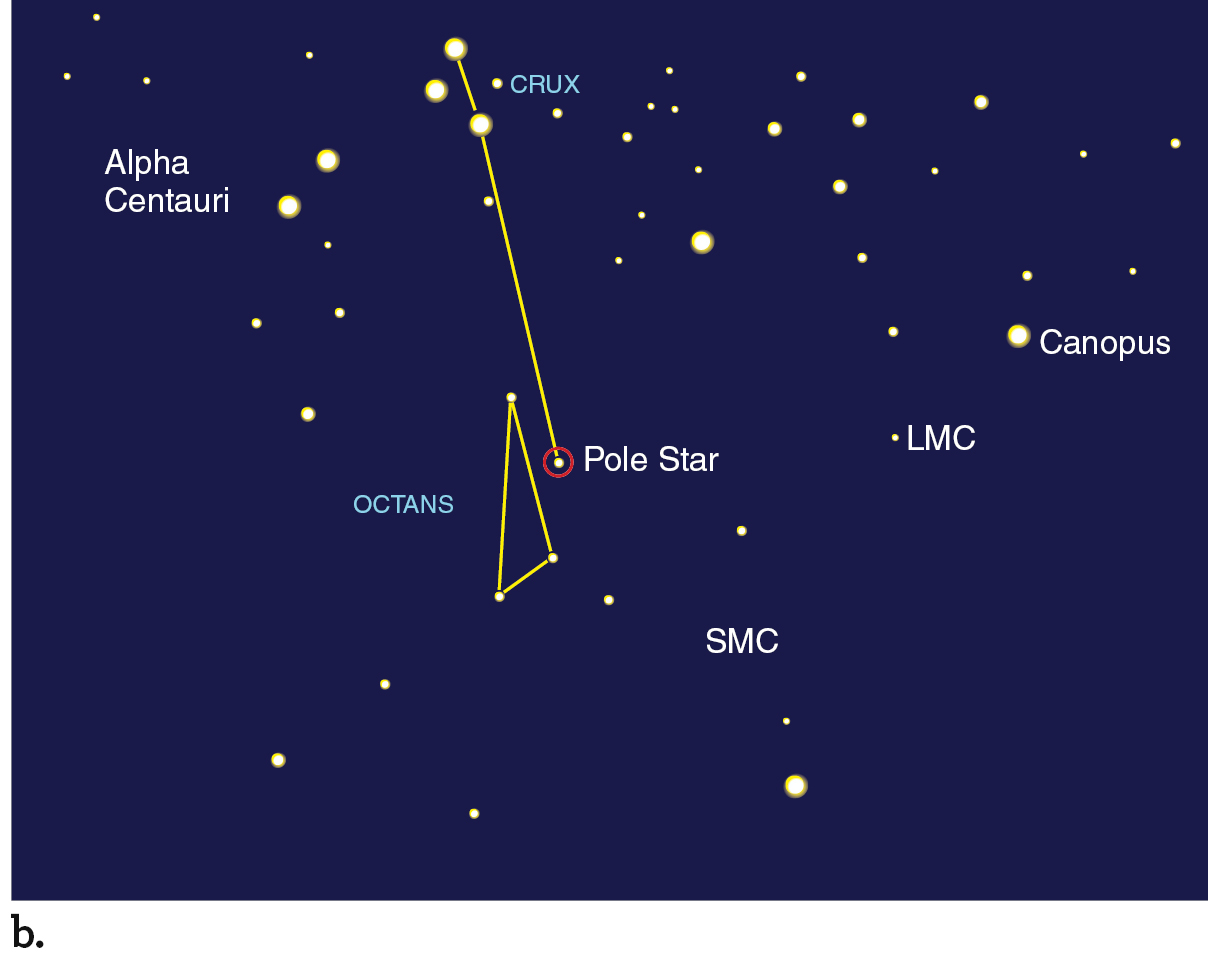
Astronomy in Action: Vocabulary of the Celestial Sphere
2.1 Earth Spins on Its Axis
Ancient humans may not have known that they were “stardust,” but they did sense a connection between their lives on Earth and the sky above. By watching the repeating patterns of the Sun, Moon, and stars in the sky, people could predict when the seasons would change and when the rains would come and the crops would grow. Some of those early observations and ideas live on today in the names of stars, in the apparent grouping of stars we call constellations, in calendars based on the Moon and Sun that many cultures still use, and in the astronomical names of the days of the week.
Across the world, the archaeological record holds evidence that ancient cultures built structures to study astronomical positions and events. Figure 2.1 shows some examples. From the 8th through 17th centuries, people used pre-telescopic astronomical observatories to study the sky for timekeeping and navigation. Many of those structures and observatories are now national historical or UNESCO World Heritage sites.
The Celestial Sphere
Aristotle and other Greek philosophers knew, in antiquity, that Earth is a sphere. However, because Earth seems stationary, they did not realize that its motion caused the changes they observed in the sky from day to day and year to year. As we explain here, Earth’s rotation on its axis determines the rising and setting of the Sun, Moon, and stars—one of the rhythms that governs life on Earth.
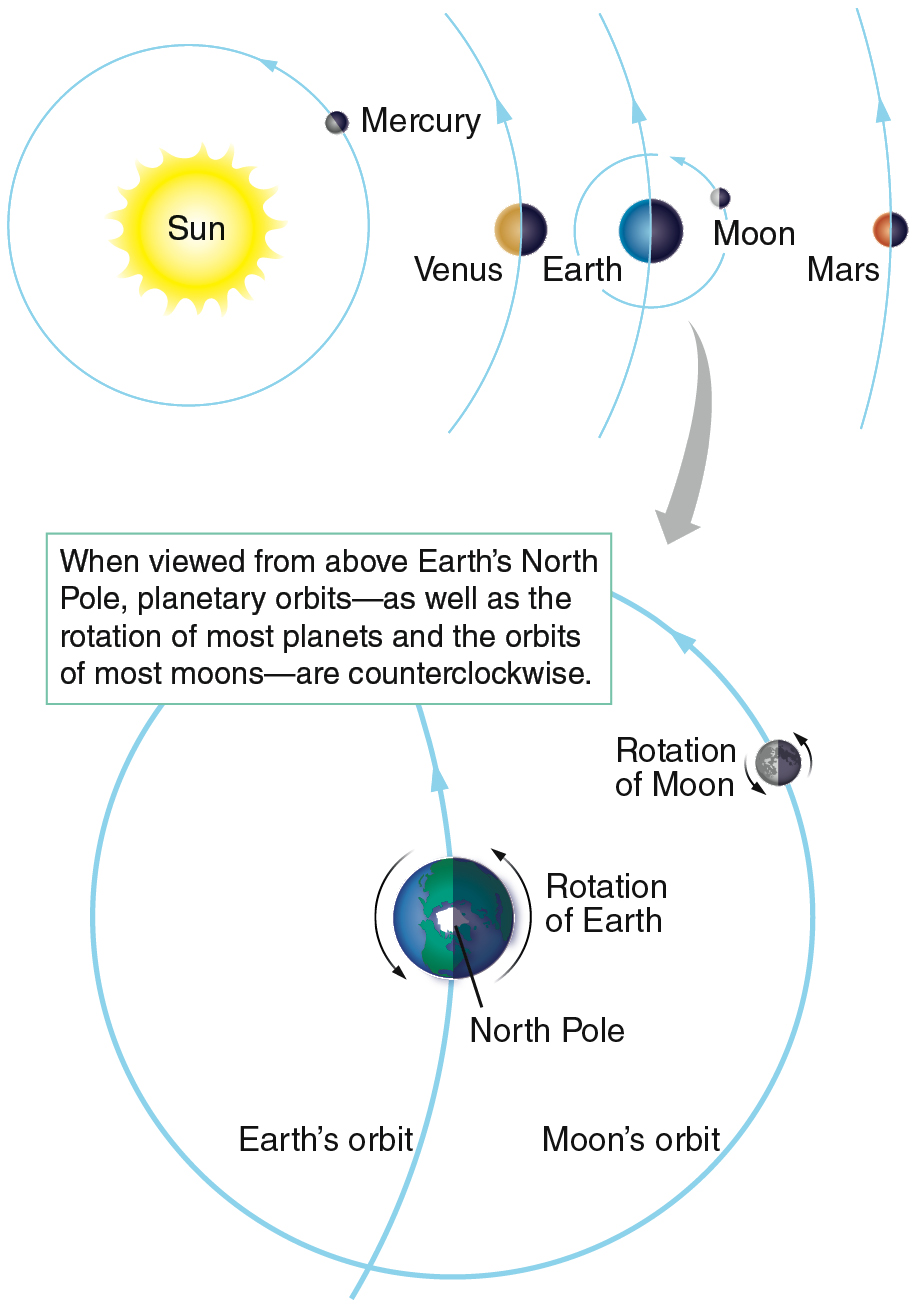
As Earth rotates about its axis, the planet’s surface is moving quite fast—about 1674 kilometers per hour (km/h) at the equator. Like the ancients, you do not feel that motion. Because the motion is uniform, you do not feel it any more than you would feel the motion of a car with a perfectly smooth ride cruising down a straight highway. Nor do you feel the direction of Earth’s spin, although the apparent daily motion of the Sun, Moon, and stars across the sky reveals that direction. Imagine that you are in space far above Earth’s North Pole, which is located at the north end of Earth’s rotation axis. From there you would see Earth complete a counterclockwise rotation, once each 24-hour period, as Figure 2.2 shows. As the rotating Earth carries an observer on the surface from west to east, objects in the sky appear to move in the opposite direction, from east to west. As seen from Earth’s surface, each object seems to move across the sky in a path called its apparent daily motion.
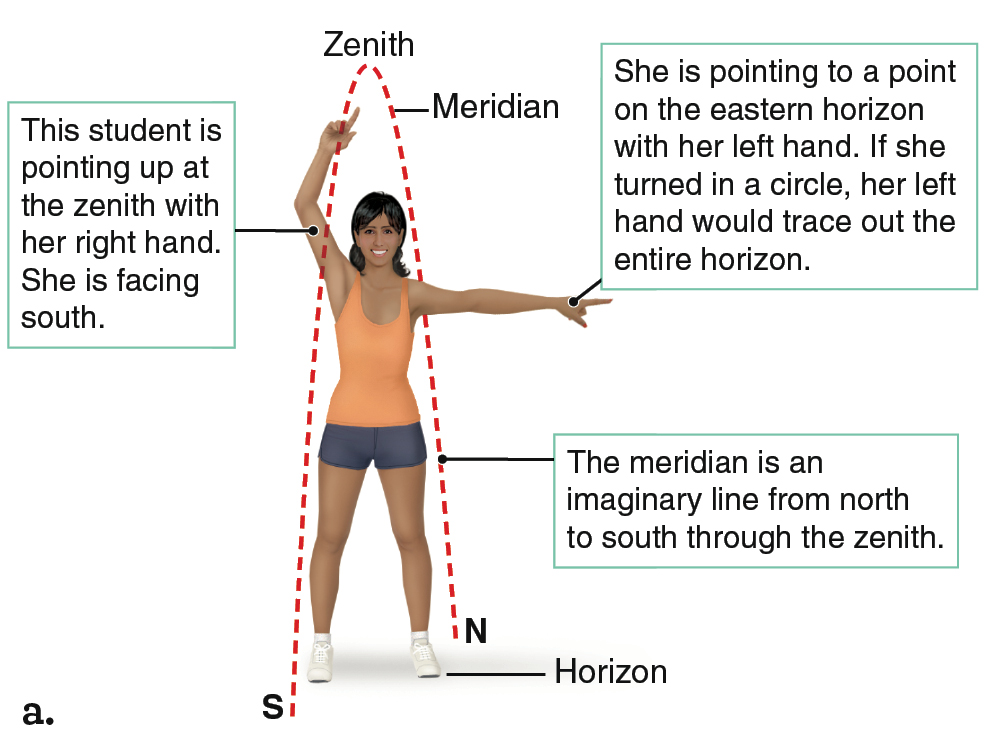
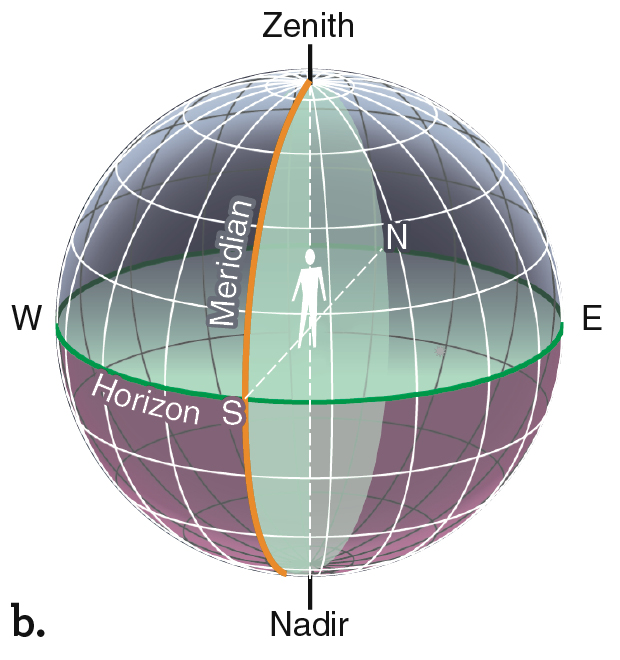
Several special terms are needed to describe the sky that you can see above you while standing on Earth. The zenith is the point in the sky directly above you (Figure 2.3a). Wherever you are on Earth, you can see only half the sky. The horizon is the boundary between the part of the sky you can see and the other half of the sky that is blocked by Earth (Figure 2.3b). You can find the horizon by standing up and pointing your right hand at the zenith and your left hand straight out from your side. Turn in a complete circle. Your left hand has traced out the entire horizon. In common language, the “horizon” is thought of as where the sky meets the ground. Objects like mountains or tall buildings can make that complicated. So astronomers ignore those complications, and consider the horizon to be perfectly straight, as if you were on a boat in the middle of a calm ocean. The meridian is an imaginary line that runs from north to south, through the zenith. It divides the sky into an eastern half and a western half. The meridian is shown as a dashed line in Figure 2.3a. The meridian line continues around the far side of Earth, through the nadir (the point directly below you), and back to the starting point due north.
To help visualize the apparent daily motions of the Sun and stars, think of the sky as a huge imaginary sphere, called the celestial sphere, with the stars painted on its surface and Earth at its center. From ancient Greek times to the Renaissance, many people believed that to be a true representation of the heavens. The celestial sphere is a useful concept because it is easy to visualize, but never forget that it is, in fact, imaginary.
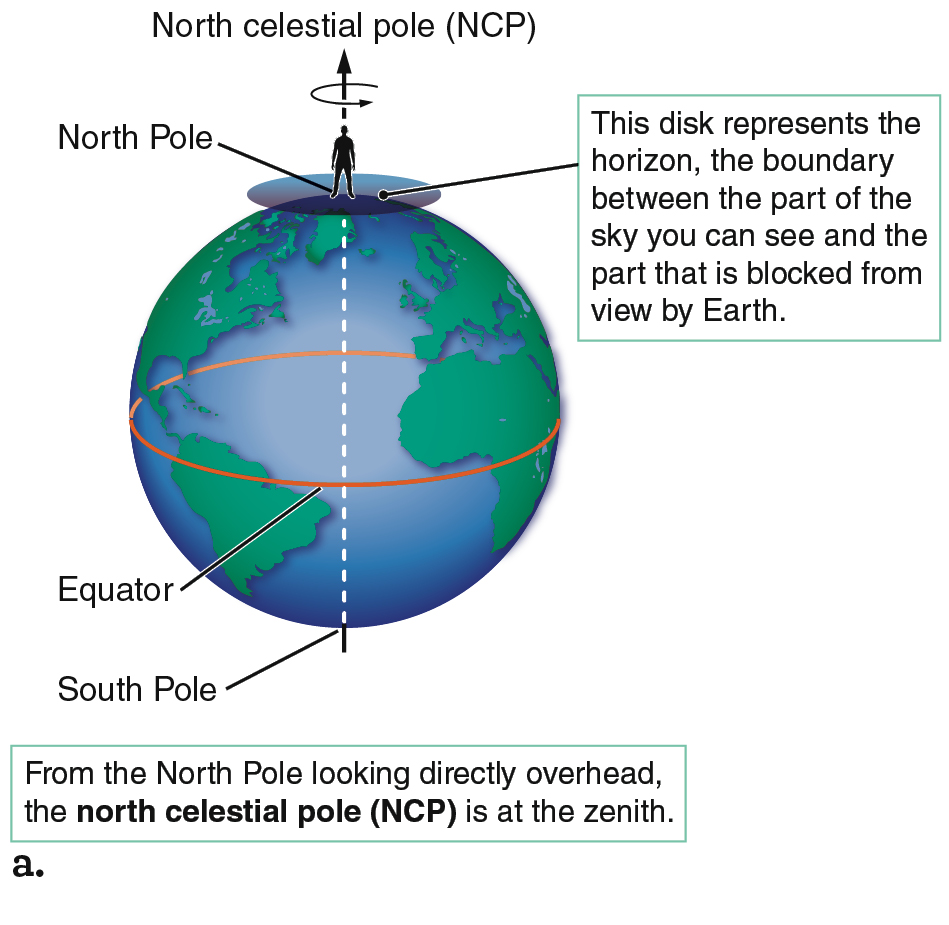
For an Earth-bound observer, each point on the celestial sphere indicates a direction in space (Figure 2.4). An observer looking straight up from Earth’s North Pole is looking in the direction of the north celestial pole (NCP). Directly above Earth’s South Pole, which is at the south end of Earth’s rotation axis, is the south celestial pole (SCP). Directly above Earth’s equator is the celestial equator, an imaginary circle that divides the sky into a northern half and a southern half. Just as Earth’s North Pole is 90° away from Earth’s equator, the north celestial pole is 90° away from the celestial equator. If you are in the Northern Hemisphere and you point one arm toward the celestial equator and one arm toward the north celestial pole, your arms will always form a right angle. The same holds true for the Southern Hemisphere: the angle between the celestial equator and the south celestial pole is always 90° as well.
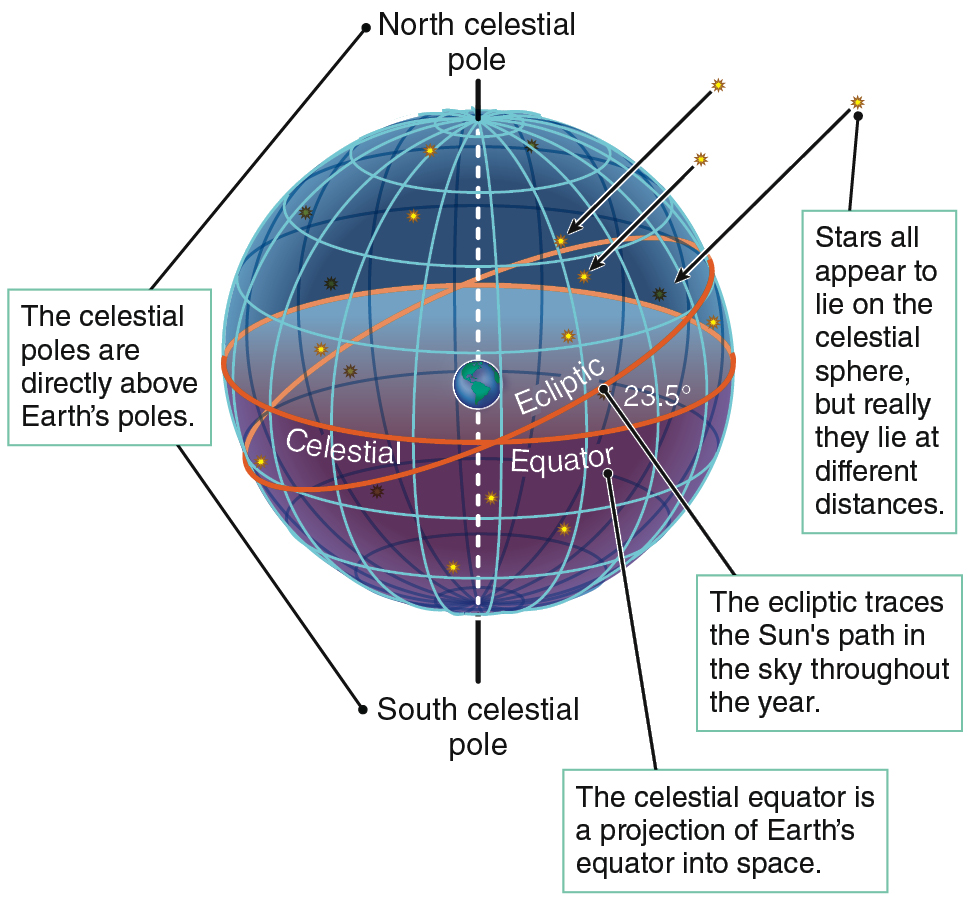
Between the celestial poles and the equator, objects have positions on the celestial sphere with coordinates analogous to latitude and longitude on Earth. Latitude indicates distance north or south from Earth’s equator. You find your latitude by imagining one line from the center of Earth to your location on the surface, and a second line from Earth’s center to the point on the equator closest to you. The angle between those two lines is your latitude. At the North Pole, for example, those two imaginary lines form a 90° angle. At the equator, they form a 0° angle. So the latitude of the North Pole is 90° north, and the latitude of the equator is 0°. The South Pole is at latitude 90° south. Similarly, on the celestial sphere, declination indicates the distance of an object north or south of the celestial equator (from 0° to ±90°).
On Earth, longitude measures position east or west from the Royal Observatory in Greenwich, England. Similarly, on the celestial sphere, right ascension is an eastward and westward measure. The ecliptic is the Sun’s path in the sky throughout the year. Notice in Figure 2.4 that the ecliptic is tilted relative to the celestial equator. The two circles in the sky intersect in two locations. Right ascension is equal to zero at one of these crossing points, and increases towards the east. Right ascension and declination are used to locate objects in the sky as precisely as anyone might require. In Appendix 7, we discuss detailed descriptions and illustrations of latitude and longitude as well as coordinates used with the celestial sphere.
Take a moment to visualize all those locations in space. To see how to use the celestial sphere, consider the Sun at noon and at midnight. Local noon occurs when the Sun crosses the meridian at your location. That is the highest point above the horizon that the Sun will reach on any given day. The highest point is almost never the zenith. You have to be in a specific place on a specific day for the Sun to be directly overhead at noon. One such place and time is at latitude 23.5° north of the equator on June 20.
From our perspective on Earth, the celestial sphere appears to rotate, carrying the Sun across the sky to its highest point at noon, over toward the west to set in the evening. In reality, the Sun remains in the same place in space through the entire 24-hour period, and Earth rotates so that any given location on Earth faces a different direction at every moment. When it is noon where you live, Earth has rotated so that you face most directly toward the Sun. Half a day later, at midnight, your location on Earth has rotated to face most directly away from the Sun. Local midnight occurs when the Sun is precisely opposite from its position at local noon.
The View from the Poles
The apparent daily motions of the stars and the Sun depend on where you live. For example, the apparent daily motions of celestial objects in a northern place such as Alaska are different from the apparent daily motions seen from a tropical island such as Hawai’i. To understand why location matters, let’s examine the view of the stars from the poles—and then use them to guide our thinking about the view of the stars from other latitudes.
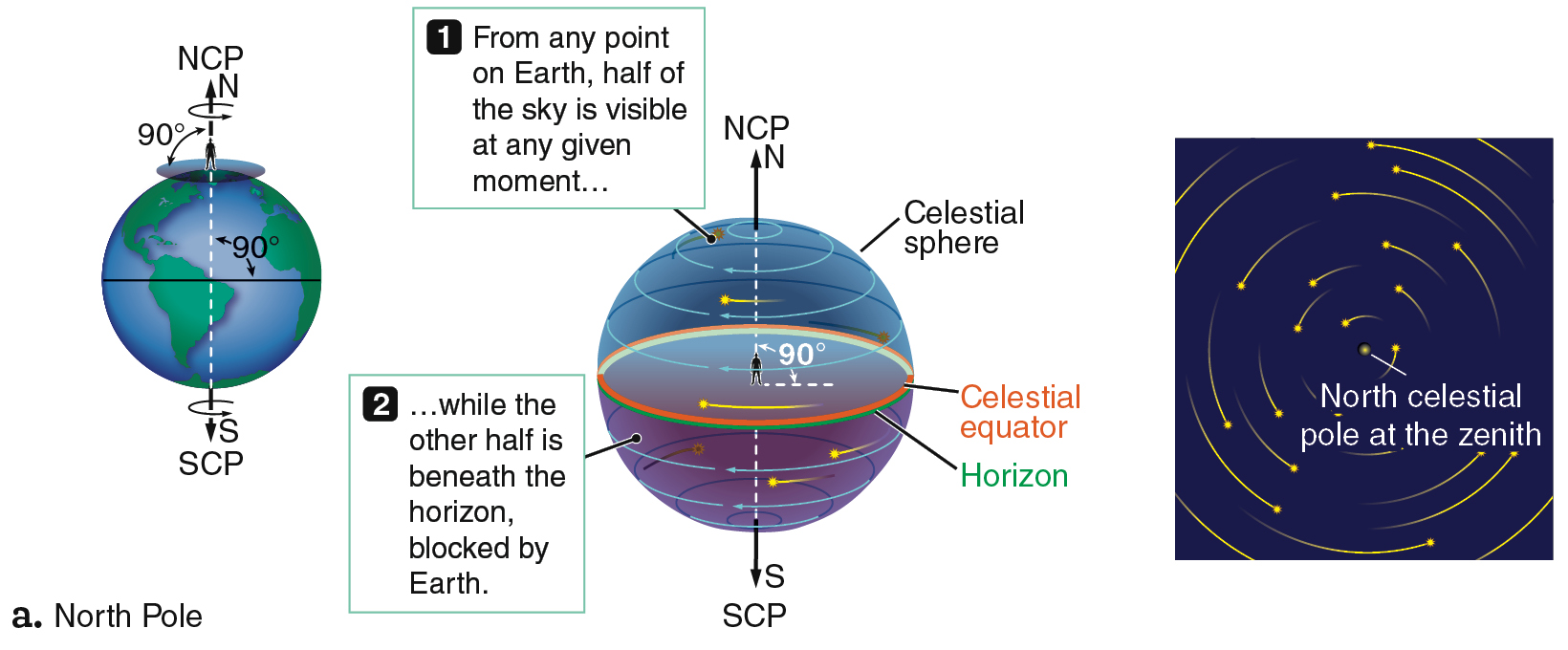
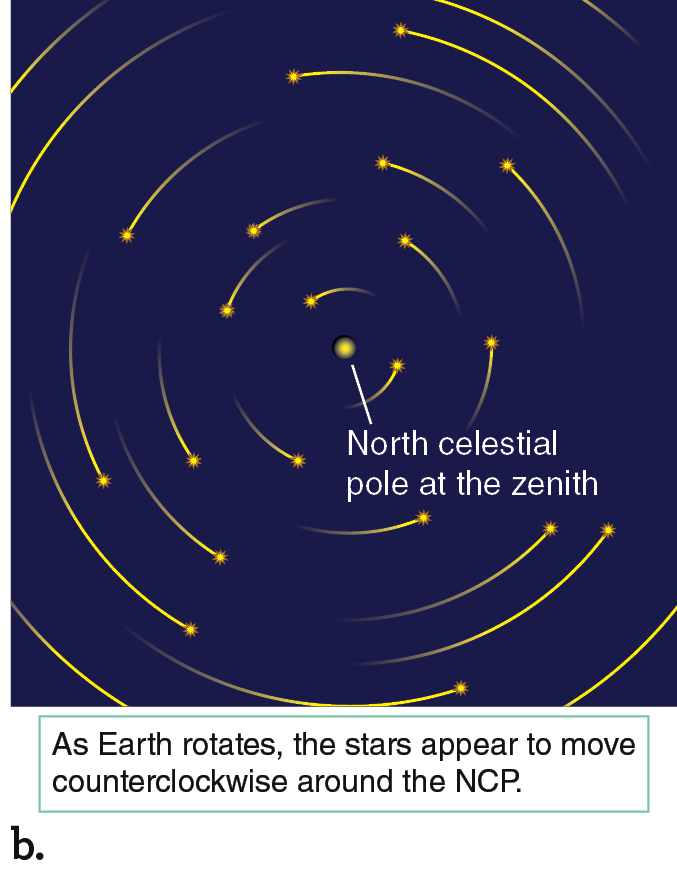
Imagine that you are the person in Figure 2.5a who is standing on the North Pole watching the sky. There, the north celestial pole is directly overhead at the zenith. You are standing where Earth’s axis of rotation intersects its surface, which is like standing at the center of a rotating carousel. As Earth rotates, the spot directly above you remains fixed over your head while everything else in the sky appears to revolve counterclockwise around that spot. Figure 2.5b depicts that view of the sky from the ground, when the Sun is below the horizon.
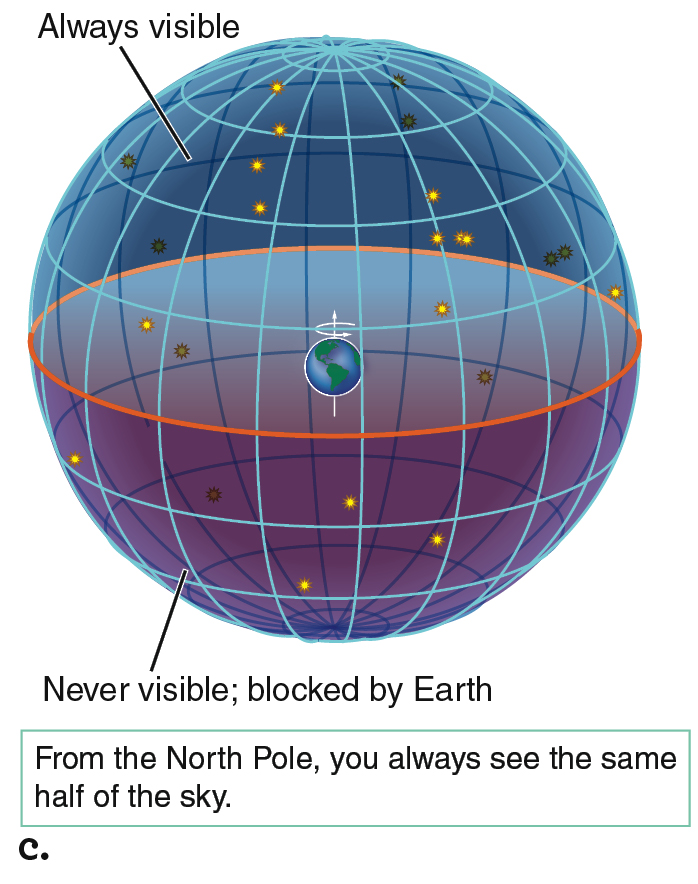
If you are standing at the North Pole, the zenith and the horizon are always indicating the same locations in space. Objects visible from the North Pole follow circular paths that always have the same altitude, or angle above the horizon. Objects close to the zenith appear to follow small circles, whereas objects near the horizon follow the largest circles (Figure 2.5b). The view from the North Pole is special: you will always see the same half of the celestial sphere from there because nothing rises or sets each day as Earth turns (Figure 2.5c).
The view from Earth’s South Pole is much the same—with two differences. First, the South Pole is on the opposite side of Earth from the North Pole, so the visible half of the sky at the South Pole is precisely the half hidden from view at the North Pole. Second, stars appear to move clockwise around the south celestial pole rather than counterclockwise as they do at the north celestial pole. To visualize why those motions are different, stand up and spin around from right to left. As you look at the ceiling, things appear to move counterclockwise, but as you look at the floor, they appear to be moving clockwise.
CHECK YOUR UNDERSTANDING 2.1a
No matter where you are on Earth, stars appear to rotate about a point called the: (a) zenith; (b) celestial pole; (c) nadir; (d) meridian.
b
The View Away from the Poles
Away from the poles, the visible half of the sky changes constantly as Earth carries you around; your horizon cuts across different points in space, and your zenith moves across the sky as Earth rotates. Suppose that you leave the North Pole to travel south to lower latitudes. Your latitude is equal to the angle of your position from the equator, as shown for the person standing at 60° north latitude in Figure 2.6.
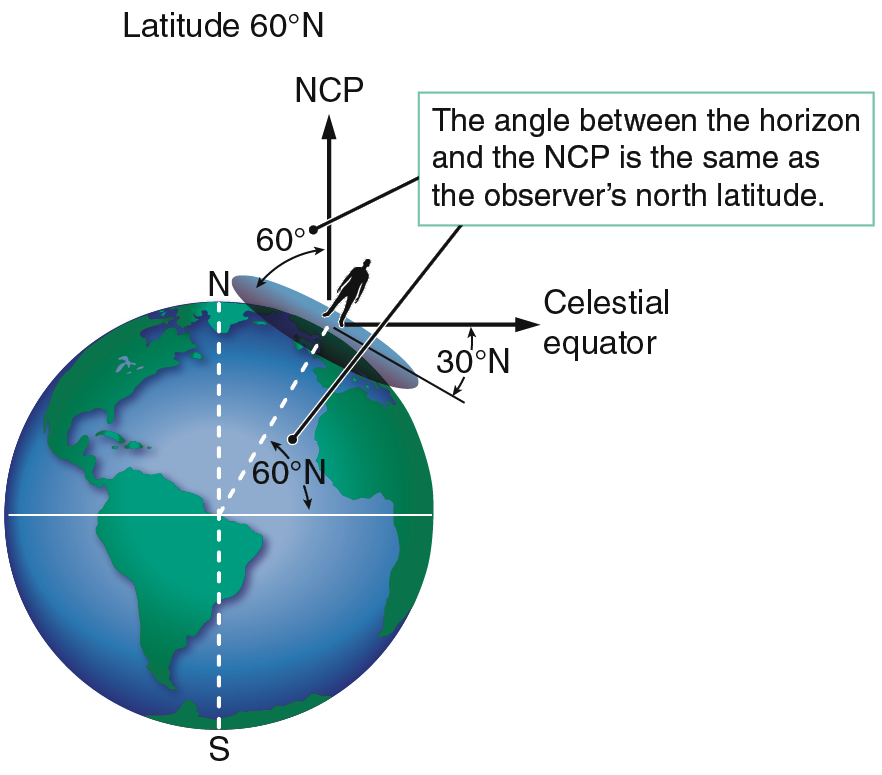
Your latitude determines the part of the sky that you can see throughout the year. As you move south from the North Pole, your zenith moves away from the north celestial pole, and your horizon moves as well. At the North Pole, the north celestial pole is 90° above the horizon (at the zenith). At a latitude of 60° north, as in Figure 2.6, the north celestial pole is 60° above the horizon. In the Northern Hemisphere, the angle between your horizon and the north celestial pole is equal to your latitude. The situation is the same in the Southern Hemisphere—your latitude is the altitude of the south celestial pole. At the equator, at a latitude of 0°, the north and south celestial poles are precisely on the horizon.
One way to solidify your understanding of the view of the sky at different latitudes is to draw pictures like the one in Figure 2.6. If you can draw a picture like that for any latitude—filling in the values for each angle in the drawing and imagining what the sky looks like from there—you are developing a working knowledge of the appearance of the sky. That knowledge will prove useful later when we discuss a variety of phenomena, such as the changing of the seasons.
Motions of the Stars and the Celestial Poles
The stars’ apparent motions about the celestial poles also differ from latitude to latitude. At the poles, all the stars are circumpolar; they go “around the pole” and never rise or set. As an observer moves farther from the poles, they will see fewer circumpolar stars. Two time-lapse views of the sky from different latitudes are shown in Figure 2.7. More stars are circumpolar for the more northern latitude, in Canada. The image taken from Utah is farther south, so it has fewer circumpolar stars. The Utah image also demonstrates the added complication that objects on the horizon often block low altitudes in the sky. Even stars that ought to be visible all the time, because they are circumpolar, might drop behind nearby objects that block the horizon.

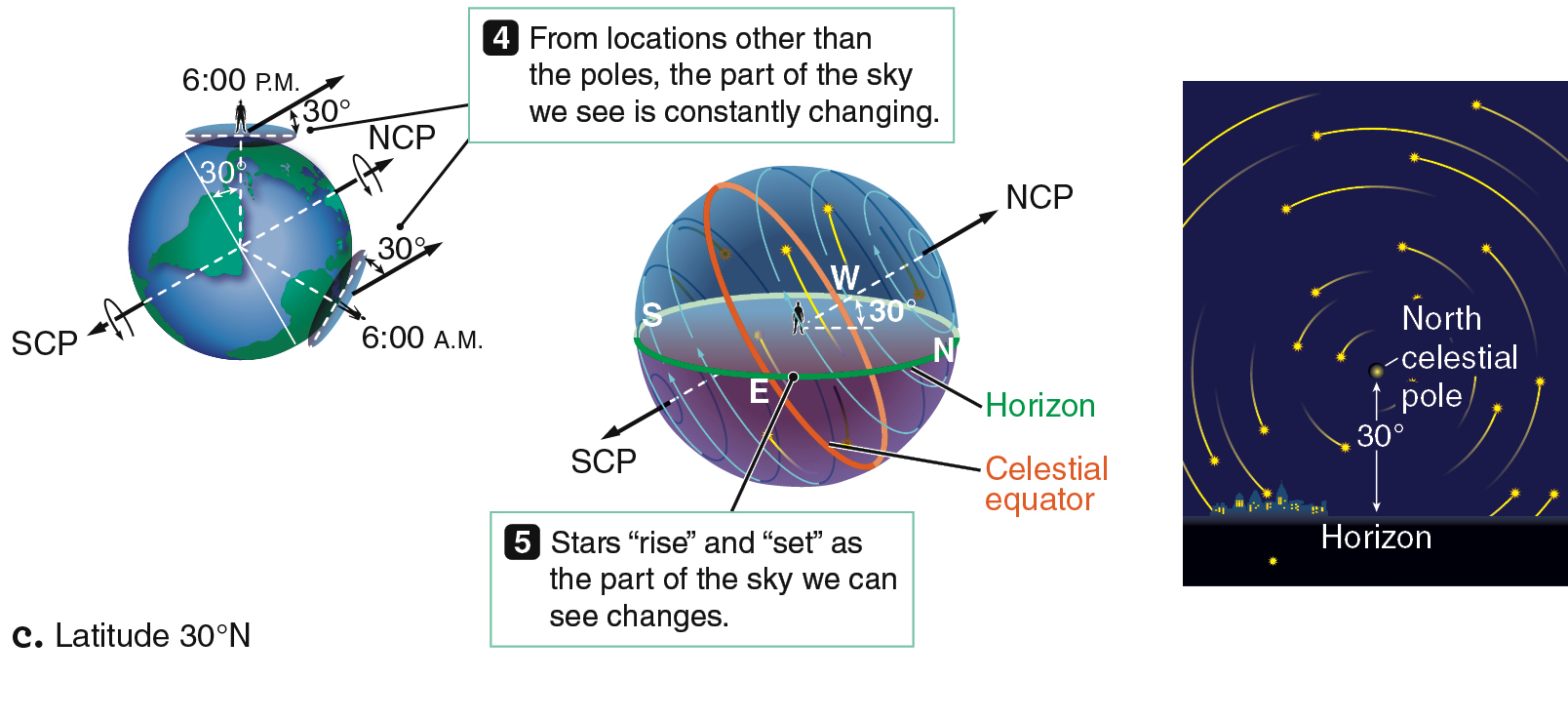
From the Canada and Utah latitudes, if we focus our attention on stars near the north celestial pole, we see much the same thing we saw from Earth’s North Pole. All the stars appear to move throughout the night in counterclockwise, circular paths around the north celestial pole. The north celestial pole is no longer directly overhead as it was at the North Pole, however, so the apparent circular paths of the stars are now tipped with respect to the horizon. (More correctly, your horizon is now tipped with respect to the apparent circular paths of the stars.)
Recall from Figure 2.6 that your latitude is equal to the altitude of the north celestial pole. Stars closer to the north celestial pole than that angle are above the horizon all the time, so they are circumpolar. Another group of stars, near the south celestial pole, are below the horizon all the time; they are never visible at all from your location. Stars between those that never rise and those that are circumpolar can be seen for only part of each 24-hour day; they appear to rise and set as Earth rotates.
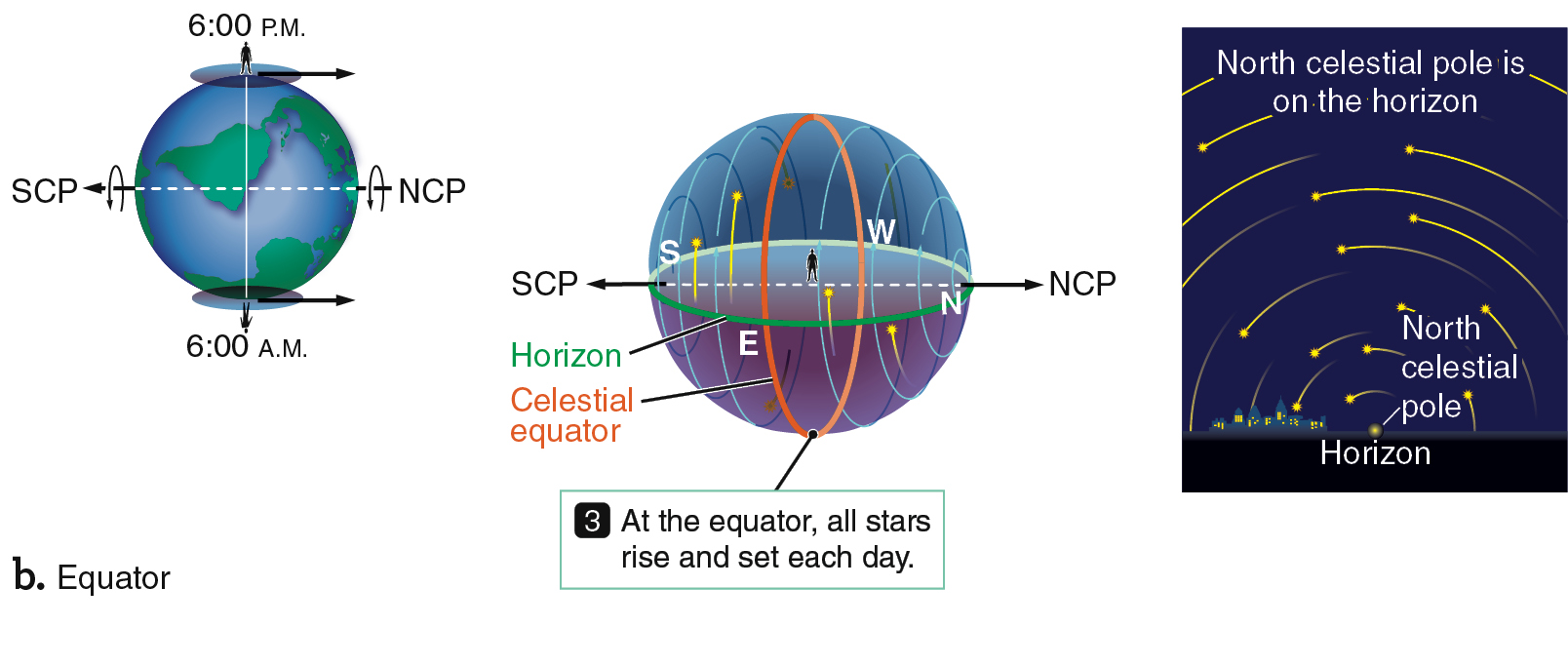
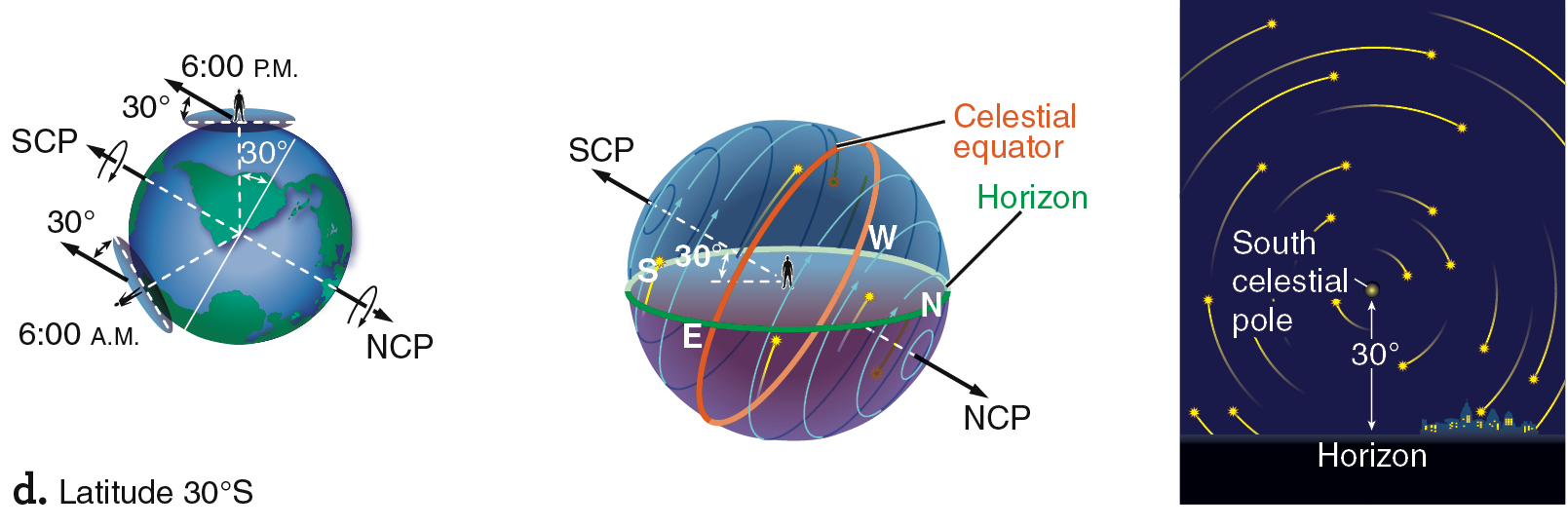
Figure 2.8 shows the orientation of the sky as seen by observers at the North Pole, the equator, 30° north, and 30° south. The view from the North Pole (Figure 2.8a) was previously shown in Figure 2.5, but it is reproduced here for ease of comparison. For an observer at the equator (Figure 2.8b), the celestial poles are both at the horizon, and all the stars are visible in a 24-hour period, rising straight up and setting straight down each day. The equator is the only place on Earth from which you can see the entire celestial sphere over the course of 24 hours.

what if . . .
What if Earth did not rotate at all relative to the stars as it orbited the Sun? What effect would that have on the science of astronomy?
From everywhere on Earth (except at the poles), half of the celestial equator is always visible above the horizon. Therefore, any object located on the celestial equator is visible half the time—above the horizon for 12 hours each day. At other latitudes, the celestial equator intersects the horizon due east and due west. Therefore, a star on the celestial equator rises due east and sets due west. Stars located north of the celestial equator rise north of east and set north of west. Stars located south of the celestial equator rise south of east and set south of west.
The middle panel of Figure 2.8c shows the path of stars above the horizon for a location 30° north of the equator. Compare the length of the arcs north of the celestial equator to those south of the celestial equator. These arcs are different lengths, so stars not on the celestial equator are above the horizon for different amounts of time. As seen from the Northern Hemisphere, stars north of the celestial equator remain above the horizon for more than 12 hours each day. The farther north the star is, the longer it stays up. Circumpolar stars are the extreme example of that phenomenon; they are always above the horizon. In contrast, stars south of the celestial equator are above the horizon for less than 12 hours each day. The farther south a star is, the less time it is visible. For an observer in the Northern Hemisphere, stars located close to the south celestial pole never rise above the horizon.
Figures 2.8c and d show that stars in the observer’s hemisphere are visible for more than half the day because more than half of each star’s path in the sky is above the horizon. In contrast, stars in the opposite hemisphere are visible for less than half the day because less than half of each star’s path in the sky is above the horizon.
working it out 2.1
How to Estimate Earth’s Size
We can use the location of the north celestial pole in the sky to estimate Earth’s size. Suppose we start out in Phoenix, Arizona, and we observe the north celestial pole to be 33.5° above the horizon. If we head north about 290 km to the Grand Canyon, the north celestial pole has risen to about 36° above the horizon. That difference between 33.5° and 36° (2.5°) is 1/144 of the way around a circle. (A circle is 360°, and 2.5°/360° = 1/144.)
That means we must have traveled 1/144 of the way around Earth’s circumference, C, by traveling the 290 km between Phoenix and the Grand Canyon. In other words,
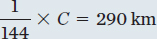
When we rearrange the expression, Earth’s circumference is given by
C = 144 × 290 km = 42,000 km
Earth’s actual circumference is just over 40,000 km, so our simple calculation was close. The circumference of a circle is equal to 2πr, where r is its radius. Earth’s radius, then, is given by
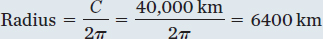
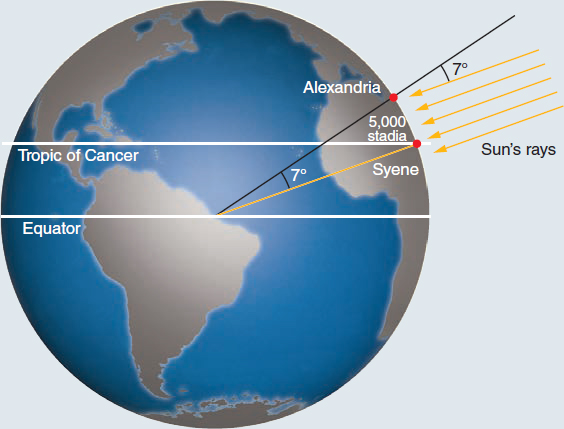
In about 230 BCE, using much the same method, the Greek astronomer Eratosthenes (276–194 BCE) was the first to accurately measure Earth’s size. As Figure 2.10 illustrates, Eratosthenes used the distance between his home city of Alexandria, Egypt, and the city of Syene (now Aswân, also in Egypt), which was 5000 “stadia.” He noticed that on the first day of summer in Syene, the sunlight reflected directly off the water in a deep well, so the Sun must have been nearly at the zenith. By measuring the shadow of the Sun from an upright stick in Alexandria, he saw that the Sun was about 7.2° south of the zenith on the same date. Assuming that Earth was spherical and that Syene was directly south of Alexandria, he determined the distance between the two cities to be 7.2° divided by 360, or 1/50 of Earth’s circumference.
Although historians know Eratosthenes concluded that the cities were 5000 stadia apart, they are still not sure of the value of his stadion unit. Other sources indicate that it may have been about 185 meters. We can use this conversion factor to compare Eratosthenes’ value to modern values:

That result is only about 16 percent higher than the modern value.
Relative Motions and Frame of Reference
Why don’t we feel motion as Earth spins on its axis and moves through space in its orbit around the Sun? The answer lies in the concept of a frame of reference, a coordinate system within which an observer measures positions and motions. The difference in motion between two individual frames of reference is called the relative motion. For example, imagine that you are riding in a car traveling down a straight section of highway at a constant speed. Under those conditions, without looking out the window or feeling road vibrations, you cannot easily tell the difference between being in the moving car and sitting in a parked car. Because everything inside the car is moving together, you can measure only the relative motions between objects in the car, and they are all zero—no motion is observed. Similarly, the resulting relative motions between objects that are near each other on Earth are zero because they have the same rotational motion. That is why we do not notice Earth’s motion.
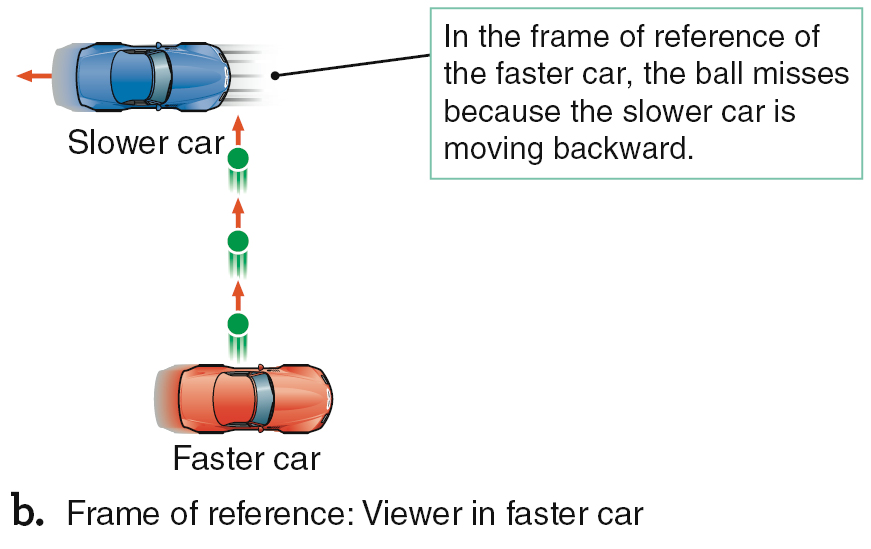
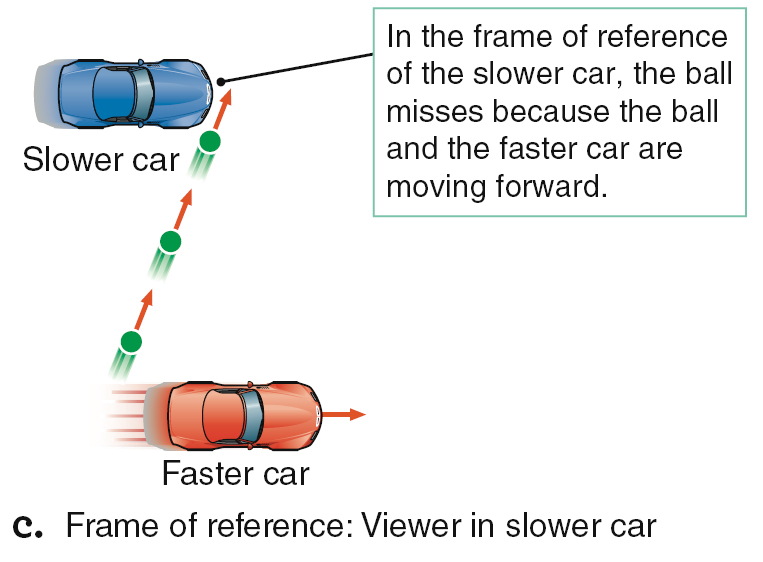
Now imagine two cars driving down the road at different speeds, as Figure 2.11a shows. For the moment, ignore any real-world complications, such as wind resistance. If you were to throw a ball from the faster-moving car directly out the side window at the slower-moving car as the two cars passed, you would miss. The ball shares the forward motion of the faster car, so the ball outruns the forward motion of the slower car. From your perspective in the faster car (Figure 2.11b), the slower car lagged behind the ball. From the slower car’s perspective (Figure 2.11c), your car and the ball sped on ahead.
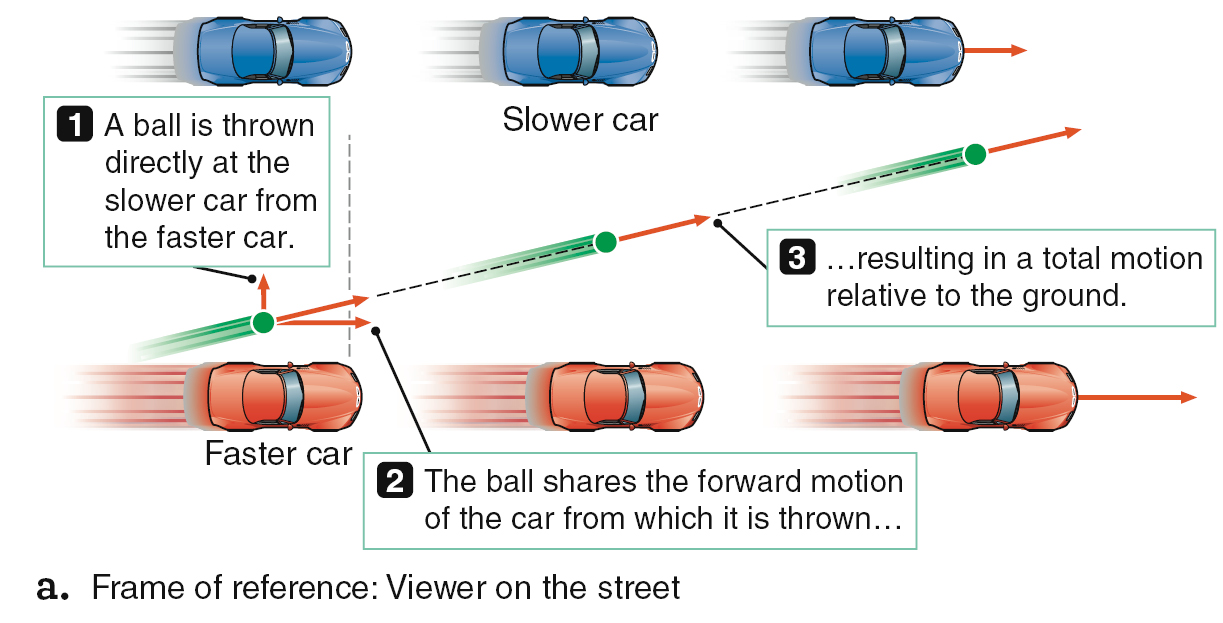
Although you cannot feel Earth’s rotation, it influences motions around you as diverse as weather patterns and the flight of artillery shells toward a distant target. Any object that travels a significant distance northward or southward above Earth’s surface will be affected. Here’s why: All points on Earth’s surface move in a circle each day around the planet’s rotation axis. That circle is larger for points near the equator and smaller for points closer to one of the poles, but all points complete their circular motion in the same amount of time: exactly 1 day. A point closer to the equator has farther to go each day than one nearer a pole does. Therefore, points nearer the equator must be moving faster than ones at higher latitude. If an object starts out at one latitude and then moves to another, that difference in the speed of the surface influences the apparent direction of the object’s motion.
Imagine a cannonball launched directly north from a point in the Northern Hemisphere, as in Figure 2.12a. Because the cannon is closer to the equator than the target, the cannon is moving toward the east faster than its target. Even though the cannonball is fired toward the north, it shares the eastward velocity of the cannon itself, just like the ball thrown from the faster car in Figure 2.11. Therefore, the cannonball is also moving toward the east faster than its target. As the cannonball flies north, it moves toward the east faster than the ground underneath it does. To an observer on the ground, the cannonball appears to curve toward the east as it outruns the eastward motion of the ground it is crossing. The farther north the cannonball flies, the greater the difference between its eastward velocity and the ground’s. The cannonball follows a path that appears to curve more and more to the east the farther north it goes. The cannonball also curves east if shot toward the south in the Southern Hemisphere, as shown in Figure 2.12a.
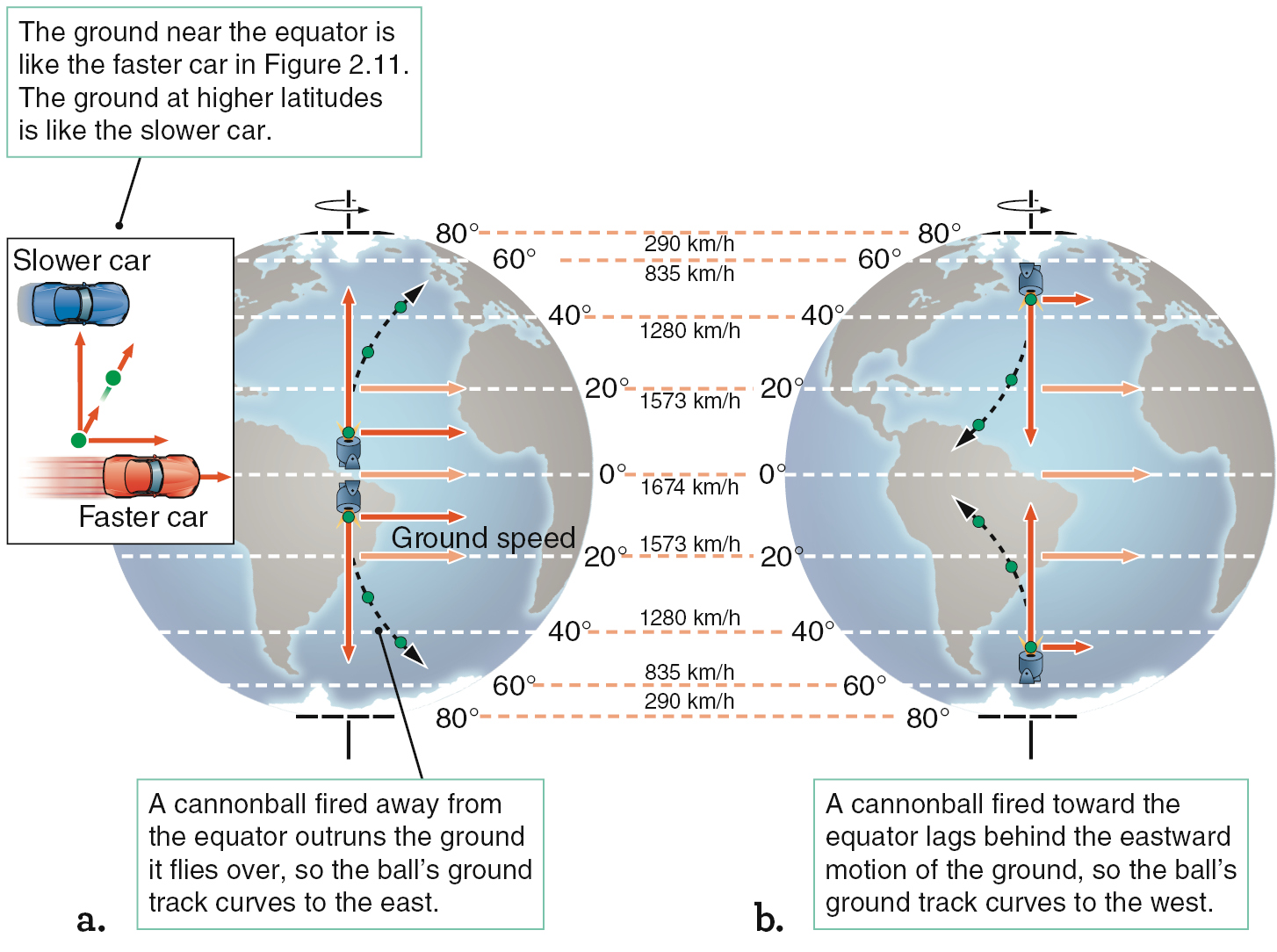
If you are located in the Northern Hemisphere and fire a cannonball south toward the equator, as in Figure 2.12b, the opposite effect will occur. Now the cannon is moving toward the east more slowly than its target. As the cannonball flies toward the south, its eastward motion lags behind that of the ground underneath it, so the cannonball appears to curve toward the west.
That curving motion of objects as a result of the difference in Earth’s rotation speeds at different latitudes is called the Coriolis effect. In the Northern Hemisphere, the Coriolis effect causes a cannonball fired north to drift to the east as seen from the ground. In other words, the cannonball appears to curve to the right, as viewed by the cannon operator. A cannonball fired south appears to curve to the west, which is also to the right as observed by the cannon operator. In the Northern Hemisphere, the Coriolis effect seems to deflect things to the right. Viewed from space, this deflection will produce a clockwise motion of weather patterns. In the Southern Hemisphere, it seems to deflect things to the left. Viewed from space, this will produce a counterclockwise motion of weather patterns. In between, at the equator itself, the Coriolis effect vanishes.
On Earth, the Coriolis effect is large enough to deflect a fly ball hit north or south deep into the outfield by about a half a centimeter. At some time or other, then, the Coriolis effect has probably affected the outcome of a baseball game. On the other hand, the story about water spiraling in different directions down a drain in different hemispheres is just a myth. On the scale of sinks or toilets, the Coriolis effect is far too small to overcome other effects, such as the shape of the basin itself. However, this story often helps people remember that the Coriolis effect works oppositely in each hemisphere, so it may be worth remembering, even if it isn’t true.
CHECK YOUR UNDERSTANDING 2.1b
If the star Polaris has an altitude of 35°, we know that: (a) our longitude is 55° east; (b) our latitude is 55° north; (c) our longitude is 35° west; (d) our latitude is 35° north.
d
Glossary
- constellations
- An imaginary image formed by patterns of stars; any of 88 defined areas on the celestial sphere that astronomers use to locate celestial objects.
- North Pole
- The location in the Northern Hemisphere where Earth’s rotation axis intersects Earth’s surface. Compare South Pole.
- apparent daily motion
- As seen from Earth’s surface, the path along which each object seems to move across the sky.
- zenith
- The point on the celestial sphere located directly overhead of an observer. Compare nadir.
- horizon
- The boundary that separates the sky from the ground.
- meridian
- The imaginary arc in the sky running from the horizon at due north through the zenith to the horizon at due south. The meridian divides the observer’s sky into eastern and western hemispheres. Compare equator.
- nadir
- The point on the celestial sphere located directly below an observer, opposite the zenith.
- celestial sphere
- An imaginary sphere with celestial objects on its inner surface and Earth at its center. The celestial sphere has no physical existence but is a convenient tool for picturing the directions in which celestial objects are seen from Earth’s surface.
- north celestial pole (NCP)
- (NCP) The northward projection of Earth’s rotation axis onto the celestial sphere. Compare south celestial pole.
- South Pole
- The location in the Southern Hemisphere where Earth’s rotation axis intersects Earth’s surface. Compare North Pole.
- south celestial pole (SCP)
- (SCP) The southward projection of Earth’s rotation axis onto the celestial sphere. Compare north celestial pole.
- equator
- The imaginary great circle on the surface of a body midway between its poles that divides the body into northern and southern hemispheres. The equatorial plane passes through the center of the body and is perpendicular to its rotation axis. Compare meridian.
- celestial equator
- The imaginary great circle that is the projection of Earth’s equator onto the celestial sphere.
- Latitude
- The angular distance north (1) or south (–) from the equatorial plane of a nearly spherical body. Compare longitude.
- declination
- A measure, analogous to latitude, that tells you the angular distance of a celestial body north or south of the celestial equator (from 0° to 690°). Compare right ascension.
- longitude
- The angular distance east (1) or west (2) from the prime meridian at Greenwich, England. Compare latitude.
- right ascension
- A measure, analogous to longitude, that tells you the angular distance of a celestial body eastward along the celestial equator from the vernal equinox. Compare declination.
- ecliptic
- 1. The apparent annual path of the Sun against the background of stars. 2. The projection of Earth’s orbital plane onto the celestial sphere.
- altitude
- The location of an object above the horizon, measured by the angle formed between an imaginary line from an observer to the object and a second line from the observer to the point on the horizon directly below the object.
- circumpolar
- Describing the part of the sky, near either celestial pole, that can always be seen above the horizon from a specific location on Earth.
- frame of reference
- A coordinate system within which an observer measures positions and motions.
- relative motion
- The difference in motion between two individual frames of reference.
- Coriolis effect
- The apparent displacement of objects in a direction perpendicular to their true motion as viewed from a rotating frame of reference. On a rotating planet, that effect arises from different latitudes’ rotating at different speeds.



 Answer
Answer Answer
Answer