3.6The Marginal Rate of Substitution

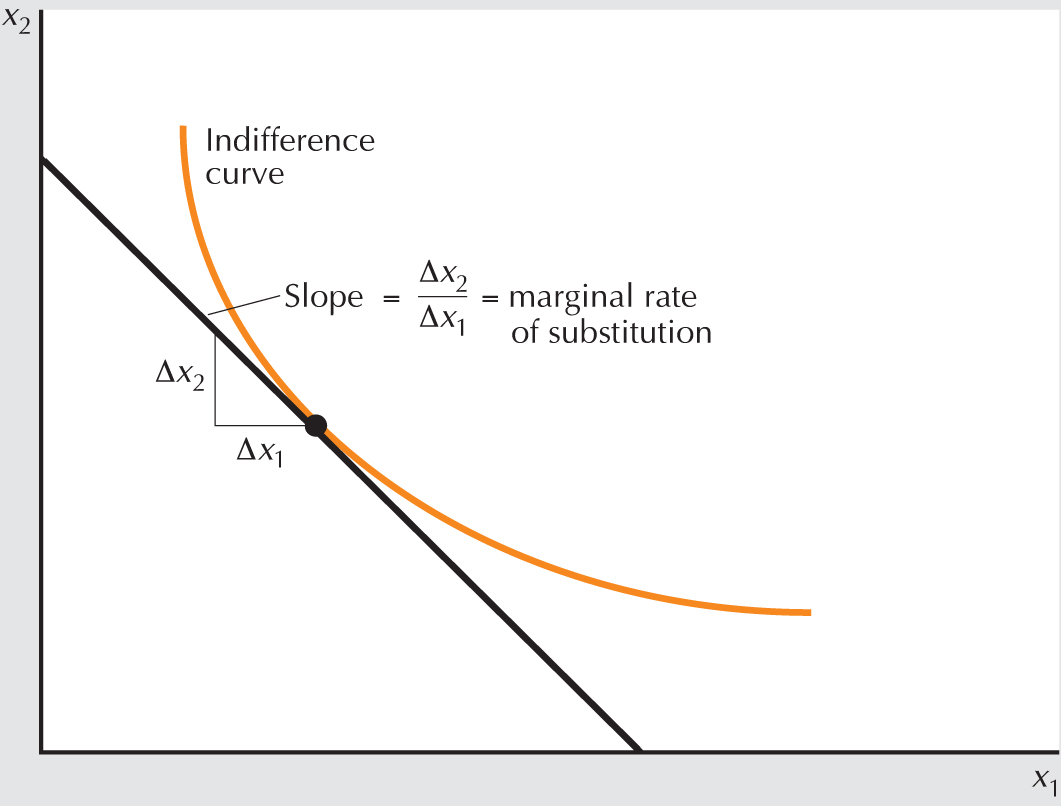
We will often find it useful to refer to the slope of an indifference curve at a particular point. This idea is so useful that it even has a name: the slope of an indifference curve is known as the marginal rate of substitution (MRS). The name comes from the fact that the MRS measures the rate at which the consumer is just willing to substitute one good for the other.

Suppose that we take a little of good 1, Δ ⁡ x 1 , away from the consumer. Then we give them Δ ⁡ x 2 , an amount that is just sufficient to put them back on their indifference curve, so they are just as well off after this substitution of x 2 for x 1 as they were before. We think of the ratio Δ ⁡ x 2 / Δ ⁡ x 1 as being the rate at which the consumer is willing to substitute good 2 for good 1.

Now think of Δ ⁡ x 1 as being a very small change—a marginal change. Then the rate Δ ⁡ x 2 / Δ ⁡ x 1 measures the marginal rate of substitution of good 2 for good 1. As Δ ⁡ x 1 gets smaller, Δ ⁡ x 2 / Δ ⁡ x 1 approaches the slope of the indifference curve, as can be seen in Figure 3.11.

The graphical interpretation of the marginal rate of substitution.
More information

The graphical interpretation of the marginal rate of substitution. An indifference curve is concave up and roughly asymptotic to the x 1 and x 2 axes. A straight line runs tangent to a point near the middle of the indifference curve. A slope triangle attached to the straight line indicates that a rightward change of delta x 1 is associated with a downward change of delta x 2. The (negative of the) slope at the tangency point, delta x 2 over delta x 1, is the marginal rate of substitution.

FIGURE 3.11 The marginal rate of substitution (MRS). The marginal rate of substitution measures the slope of the indifference curve.

When we write the ratio Δ ⁡ x 2 / Δ ⁡ x 1 , we will always think of both the numerator and the denominator as being small numbers—as describing marginal changes from the original consumption bundle. Thus the ratio defining the MRS will always describe the slope of the indifference curve: the rate at which the consumer is just willing to substitute a little more consumption of good 2 for a little less consumption of good 1.

One slightly confusing thing about the MRS is that it is typically a negative number. We’ve already seen that monotonic preferences imply that indifference curves must have a negative slope. Since the MRS is the numerical measure of the slope of an indifference curve, it will naturally be a negative number.

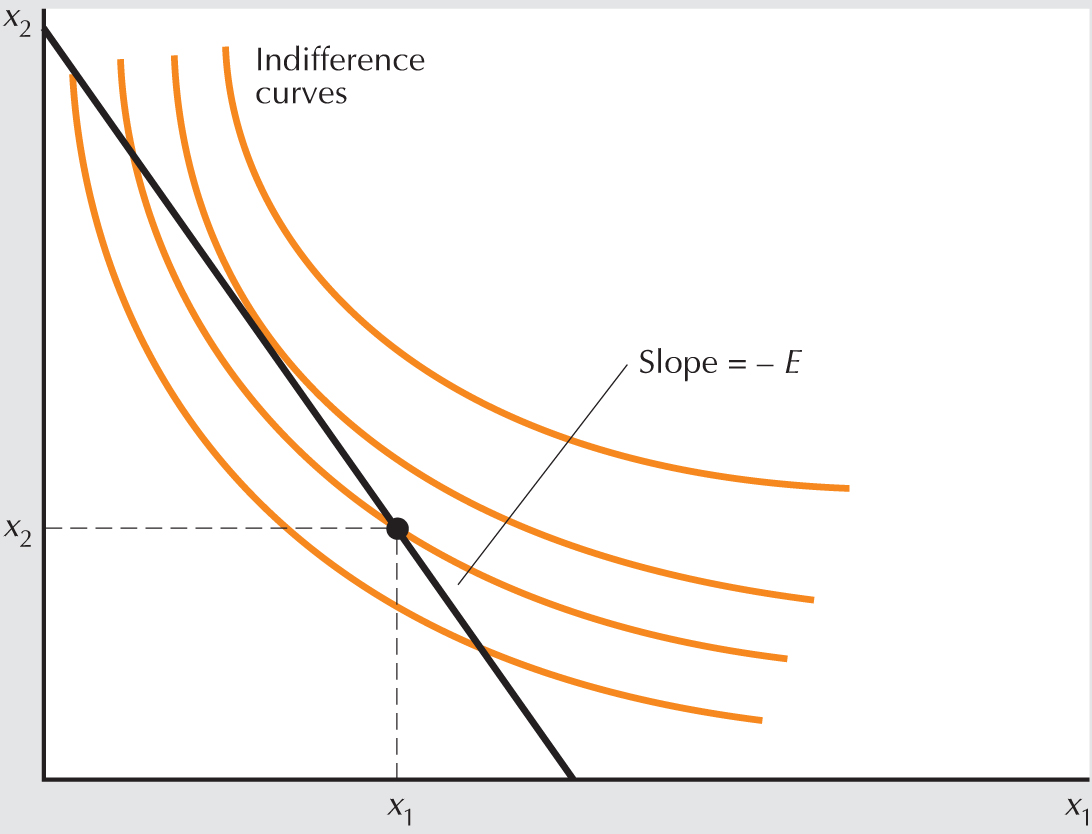
The marginal rate of substitution measures an interesting aspect of the consumer’s behavior. Suppose that the consumer has well-behaved preferences, that is, preferences that are monotonic and convex, and that the consumer is currently consuming some bundle ( x 1 , x 2 ) . We now will offer them a trade: they can exchange good 1 for 2, or good 2 for 1, in any amount at a “rate of exchange” of E .

That is, if the consumer gives up Δ ⁡ x 1 units of good 1, they can get E Δ ⁡ x 1 units of good 2 in exchange. Or, conversely, if they give up Δ ⁡ x 2 units of good 2, they can get Δ ⁡ x 2 / E units of good 1. Geometrically, we are offering the consumer an opportunity to move to any point along a line with slope − E that passes through ( x 1 , x 2 ) , as depicted in Figure 3.12. Moving up and to the left from ( x 1 , x 2 ) involves exchanging good 1 for good 2, and moving down and to the right involves exchanging good 2 for good 1. In either movement, the exchange rate is E . Since exchange always involves giving up one good in exchange for another, the exchange rate E corresponds to a slope of − E .

We can now ask what the rate of exchange would have to be in order for the consumer to want to stay put at ( x 1 , x 2 ) . To answer this question, we simply note that any time the exchange line crosses the indifference curve, there will be some points on that line that are preferred to ( x 1 , x 2 ) —that lie above the indifference curve. Thus, if there is to be no movement from ( x 1 , x 2 ) , the exchange line must be tangent to the indifference curve. That is, the slope of the exchange line, − E , must be the slope of the indifference curve at ( x 1 , x 2 ) . At any other rate of exchange, the exchange line would cut the indifference curve and thus would allow the consumer to move to a more preferred point.

Four indifference curves are concave up and each roughly asymptotic to the x 1 and x 2 axes.
More information

Four indifference curves are concave up and each roughly asymptotic to the x 1 and x 2 axes. A straight line with a fairly steep slope of negative E crosses one of the curves at point x 1 x 2. This straight line runs tangent to another indifference curve that lies up and to the right from the first one. The point of tangency is up and to the left from point x 1 x 2.

FIGURE 3.12 Trading at an exchange rate. Here we are allowing the consumer to trade the goods at an exchange rate E , which implies that the consumer can move along a line with slope − E .

Thus the slope of the indifference curve, the marginal rate of substitution, measures the rate at which the consumer is just on the margin of trading or not trading. At any rate of exchange other than the MRS, the consumer would want to trade one good for the other. But if the rate of exchange equals the MRS, the consumer wants to stay put.