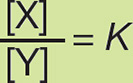CATALYSIS AND THE USE OF ENERGY BY CELLS
One property of living things above all makes them seem almost miraculously different from nonliving matter: they create and maintain order in a universe that is tending always to greater disorder (Figure 2–12). To create this order, the cells in a living organism must perform a never-ending stream of chemical reactions. In some of these reactions, small organic molecules—amino acids, sugars, nucleotides, and lipids—are being taken apart or modified to supply the many other small molecules that the cell requires. In other reactions, small molecules are being used to construct an enormously diverse range of proteins, nucleic acids, and other macromolecules that endow living systems with all of their most distinctive properties. Each cell can be viewed as a tiny chemical factory, performing many millions of reactions every second.
Cell Metabolism Is Organized by Enzymes
The chemical reactions that a cell carries out would normally proceed at an appreciable rate only at much higher temperatures than those existing inside cells. For this reason, each reaction requires a specific boost in chemical reactivity. This requirement is crucial, because it allows the cell to control its chemistry. The control is exerted through specialized biological catalysts. These are almost always proteins called enzymes, although RNA catalysts also exist, called ribozymes. Each enzyme accelerates, or catalyzes, just one of the many possible kinds of reactions that a particular molecule might undergo. Enzyme-catalyzed reactions are connected in series, so that the product of one reaction becomes the starting material, or substrate, for the next (Figure 2–13). Long linear reaction pathways are in turn linked to one another, forming a maze of interconnected reactions that enable the cell to survive, grow, and reproduce.

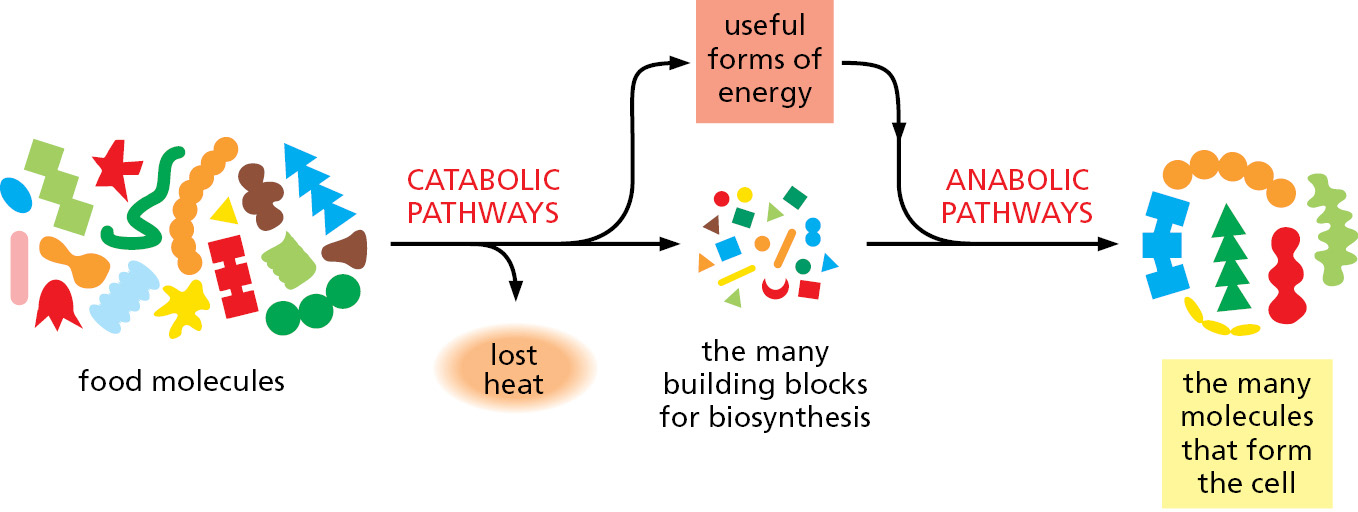
Two opposing streams of chemical reactions occur in cells: (1) the catabolic pathways break down foodstuffs into smaller molecules, thereby generating both a useful form of energy for the cell and some of the small molecules that the cell needs as building blocks; (2) the anabolic, or biosynthetic, pathways use the small molecules plus the energy harnessed by catabolism to drive the synthesis of the many other molecules that form the cell. Together these two sets of reactions constitute the metabolism of the cell (Figure 2–14).
The many details of cell metabolism form the traditional subject of biochemistry. Most of these details need not concern us here. But the general principles by which cells obtain energy from their environment and use it to create order are central to cell biology. We begin with a discussion of why a constant input of energy is needed to sustain all living things.
Biological Order Is Made Possible by the Release of Heat Energy from Cells
The universal tendency of things to become disordered is a fundamental law of physics—the second law of thermodynamics—which states that in the universe or in any isolated system (a collection of matter that is completely isolated from the rest of the universe), the degree of disorder always increases. This law has such profound implications for life that we will restate it in several ways.
For example, we can present the second law in terms of probability by stating that systems will change spontaneously toward those arrangements that have the greatest probability. If we consider a box of 100 coins all lying heads-up, a series of accidents that disturbs the box will tend to move the arrangement toward a mixture of 50 heads and 50 tails. The reason is simple: there is a huge number of possible arrangements of the individual coins in the mixture that can achieve the 50–50 result, but only one possible arrangement that keeps all of the coins oriented heads-up. Because the 50–50 mixture is therefore the most probable, we say that it is more “disordered.” For the same reason, it is a common experience that one’s living space will become increasingly disordered without intentional effort: the movement toward disorder is a spontaneous process, requiring a periodic effort to reverse it (Figure 2–15).

The amount of disorder in a system can be quantified and expressed as the entropy of the system: the greater the disorder, the greater the entropy. Thus, another way to express the second law of thermodynamics is to say that systems will change spontaneously toward arrangements with greater entropy.
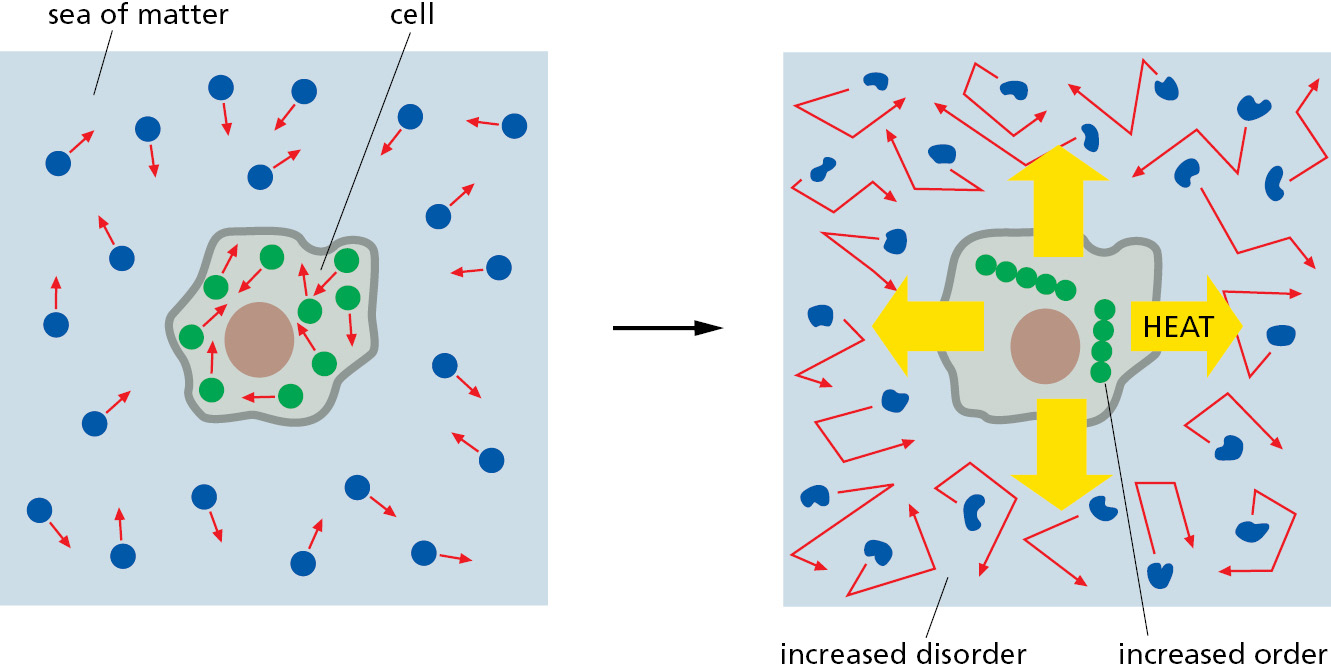
Living cells—by surviving, growing, and forming complex organisms—are generating order and thus might appear to defy the second law of thermodynamics. How is this possible? The answer is that a cell is not an isolated system: it takes in energy from its environment in the form of the chemical bonds in food or as photons from the Sun (or even, as in some chemosynthetic bacteria, from inorganic molecules alone). It then uses this energy to generate order within itself. Critically, during the chemical reactions that generate order, the cell converts part of the energy it uses into heat. The heat is discharged into the cell’s environment and disorders the surroundings. As a result, the total entropy—that of the cell plus its surroundings—increases, as demanded by the second law of thermodynamics.
To understand the principles governing these energy conversions, think of a cell surrounded by a sea of matter representing the rest of the universe. As the cell lives and grows, it creates internal order. But it constantly releases heat energy as it synthesizes molecules and assembles them into cell structures. Heat is energy in its most disordered form—the random jostling of molecules. When the cell releases heat to the sea, it increases the intensity of molecular motions there (thermal motion)—thereby increasing the randomness, or disorder, of the sea. The second law of thermodynamics is satisfied because the increase in the amount of order inside the cell is always more than compensated for by an even greater decrease in order (increase in entropy) in the surrounding sea of matter (Figure 2–16).
Where does the heat that the cell releases come from? Here we encounter another important law of thermodynamics. The first law of thermodynamics states that energy can be converted from one form to another, but that it cannot be created or destroyed. Figure 2–17 illustrates some interconversions between different forms of energy. The amount of energy in different forms will change as a result of the chemical reactions inside the cell, but the first law tells us that the total amount of energy must always be the same. For example, an animal cell takes in foodstuffs and converts some of the energy present in the chemical bonds between the atoms of these food molecules (chemical-bond energy) into the random thermal motion of molecules (heat energy)—it is this heat that keeps our bodies warm.
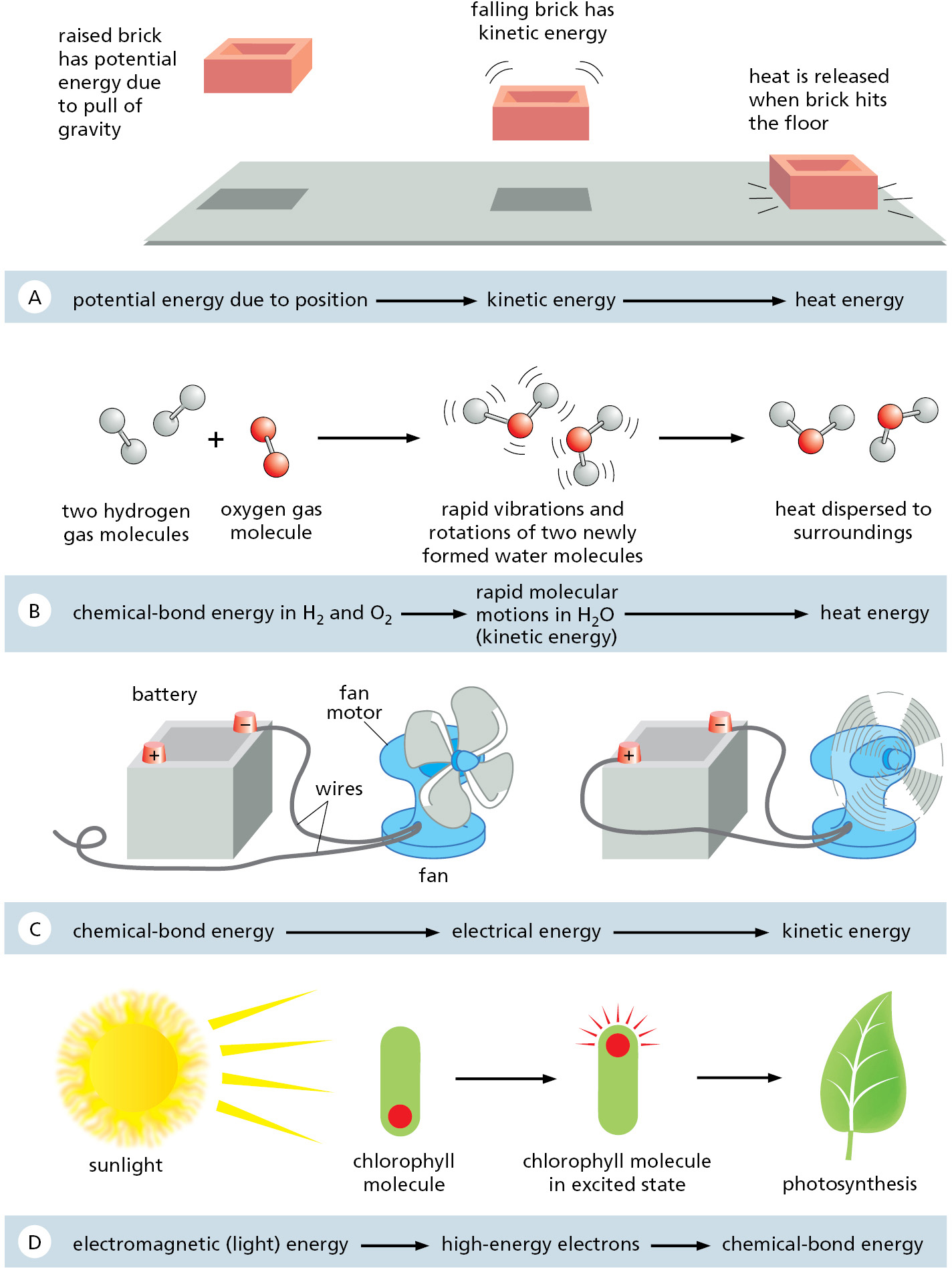
The cell cannot derive any benefit from the heat energy it releases unless the heat-generating reactions inside the cell are directly linked to the processes that generate molecular order. It is the tight coupling of heat production to an increase in order that distinguishes the metabolism of a cell from the wasteful burning of fuel in a fire. Later, we illustrate how this coupling occurs. For now, it is sufficient to recognize this critical fact: a direct linkage of the “controlled burning” of food molecules to the generation of biological order is required for cells to create and maintain an island of order in a universe tending toward chaos.
Cells Obtain Energy by the Oxidation of Organic Molecules
All animal and plant cells are powered by energy stored in the chemical bonds of organic molecules, whether they are sugars that a plant has photosynthesized as food for itself or the mixture of large and small molecules that an animal has eaten. Organisms must extract this energy in usable form to live, grow, and reproduce. In both plants and animals, energy is extracted from food molecules by a process of gradual oxidation, or controlled burning.
Earth’s atmosphere contains a great deal of oxygen, and in the presence of oxygen the most energetically stable form of carbon is CO2 and that of hydrogen is H2O. A cell is therefore able to obtain energy from sugars or other organic molecules by allowing their carbon and hydrogen atoms to combine with oxygen to produce CO2 and H2O, respectively—a process called aerobic respiration.
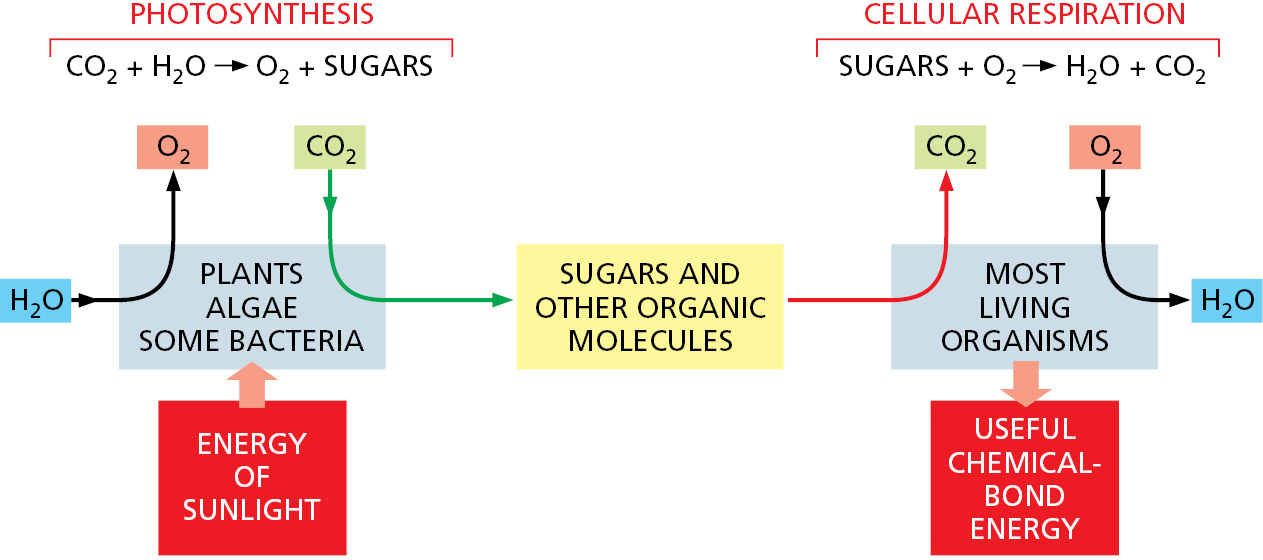
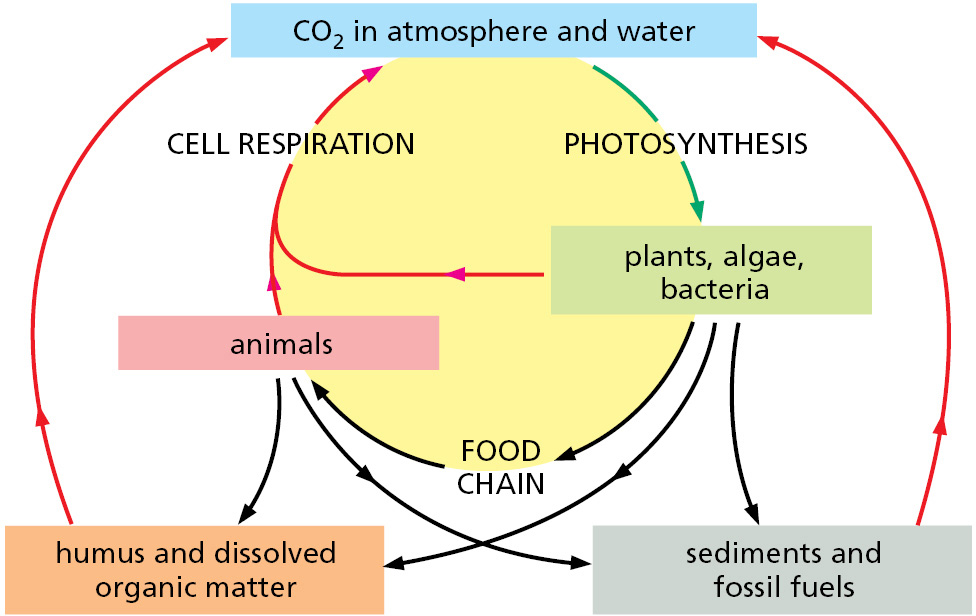
Photosynthesis (discussed in detail in Chapter 14) and respiration are complementary processes (Figure 2–18). This means that the transactions between plants and animals are not all one way. Plants, animals, and microorganisms have existed together on this planet for so long that many of them have become an essential part of the others’ environments. The oxygen released by photosynthesis is consumed in the combustion of organic molecules during aerobic respiration. And some of the CO2 molecules that are fixed today into organic molecules by photosynthesis in a green leaf were yesterday released into the atmosphere by the respiration of an animal—or by the respiration of a fungus or bacterium decomposing dead organic matter. We therefore see that carbon utilization forms a huge cycle that involves the biosphere (all of the living organisms on Earth) as a whole (Figure 2–19). Similarly, atoms of nitrogen, phosphorus, and sulfur move between the living and nonliving worlds in cycles that involve plants, algae, animals, fungi, and bacteria.
The first cells on Earth are thought to have been capable of neither photosynthesis nor respiration (discussed in Chapter 14). However, photosynthesis must have preceded respiration on Earth, because there is strong evidence that billions of years of photosynthesis were required before O2 had been released in sufficient quantity to create an atmosphere rich in this gas. (Earth’s atmosphere currently contains 21% O2.)
As indicated in Chapter 1, the total biomass on Earth is estimated to contain ∼550 gigatons (1015 grams) of carbon (Gt C), of which 450 Gt C are plants, 70 are bacteria, 7 are archaea, and 2 are animals (see Figure 1–14).
Oxidation and Reduction Involve Electron Transfers
The cell does not oxidize organic molecules in one step, as occurs when organic material is burned in a fire. Through the use of enzyme catalysts, metabolism takes these molecules through a large number of reactions that only rarely involve the direct addition of oxygen. Before we consider some of these reactions and their purpose, we discuss what is meant by the process of oxidation.
Oxidation refers to more than the addition of oxygen atoms; the term applies more generally to any reaction in which electrons are transferred from one atom to another. Oxidation in this sense refers to the removal of electrons, and reduction—the converse of oxidation—means the addition of electrons. Thus, Fe2+ is oxidized if it loses an electron to become Fe3+, and a chlorine atom is reduced if it gains an electron to become Cl–. Because the number of electrons is conserved (no loss or gain) in a chemical reaction, oxidation and reduction always occur simultaneously; that is, if one molecule gains an electron in a reaction (reduction), a second molecule loses the electron (oxidation). When a sugar molecule is oxidized to CO2 and H2O, for example, the O2 molecules involved in forming H2O gain electrons and thus are said to have been reduced.
Why is a “gain” of electrons referred to as a “reduction”? The term arose before anything was known about the movement of electrons. Originally, reduction reactions involved a liberation of oxygen—for example, when metals are extracted from ores by heating—which caused the samples to become lighter; in other words, “reduced” in mass.
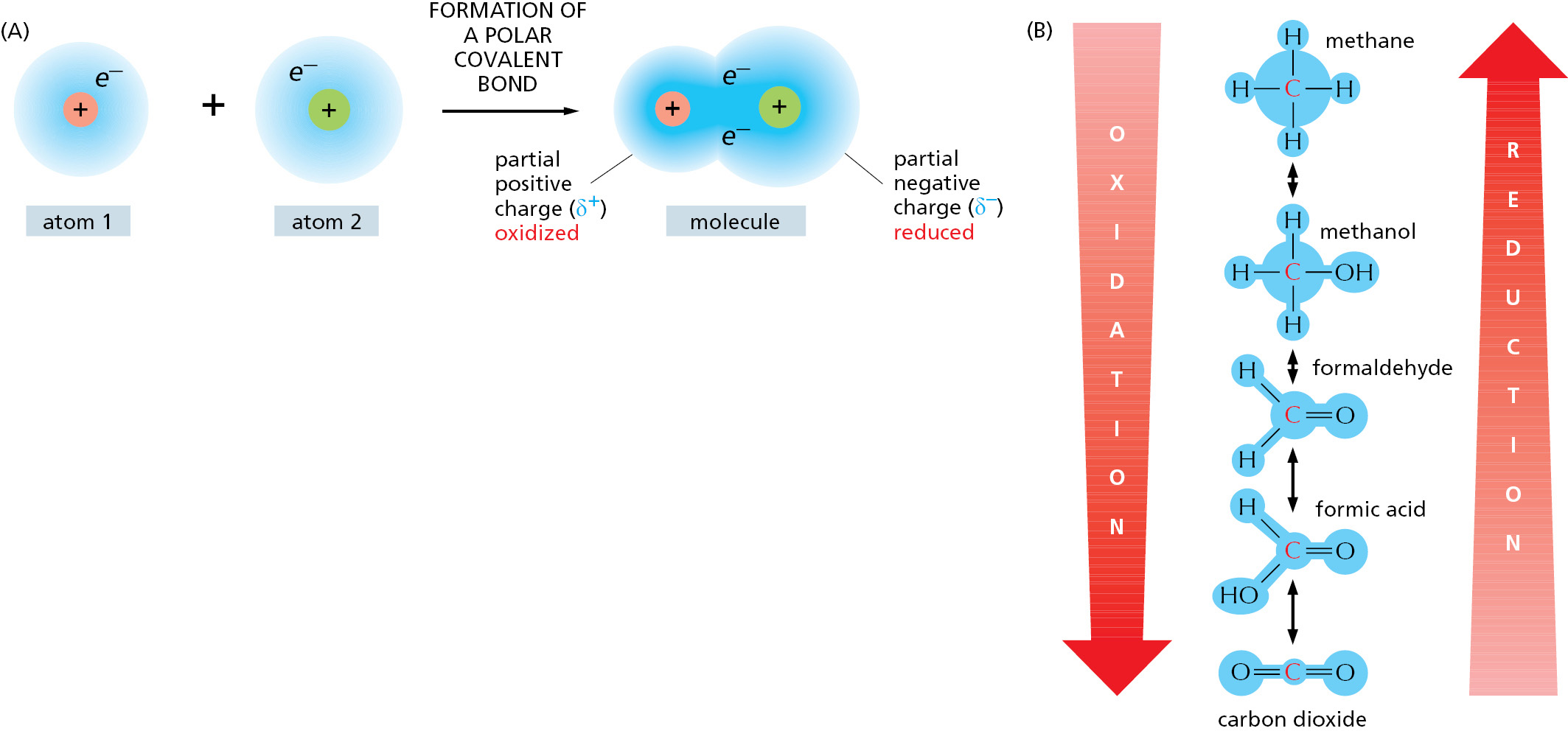
It is important to recognize that the terms “oxidation” and “reduction” apply even when there is only a partial shift of electrons between atoms linked by a covalent bond (Figure 2–20). When a carbon atom becomes covalently bonded to an atom with a strong affinity for electrons, such as oxygen, chlorine, or sulfur, for example, it gives up more than its equal share of electrons and forms a polar covalent bond. Because the positive charge of the carbon nucleus is now somewhat greater than the negative charge of its electrons, the atom acquires a partial positive charge and is said to be oxidized. Conversely, a carbon atom in a C–H linkage has slightly more than its share of electrons, and so it is said to be reduced.
When a molecule in a cell picks up an electron (e–), it often picks up a proton (H+) at the same time (protons being freely available in water). The net effect in this case is to add a hydrogen atom to the molecule.
A + e– + H+ → AH
Even though a proton plus an electron is involved (instead of just an electron), such hydrogenation reactions are reductions, and the reverse dehydrogenation reactions are oxidations. It is especially easy to tell whether an organic molecule is being oxidized or reduced: reduction is occurring if its number of C–H bonds increases, whereas oxidation is occurring if its number of C–H bonds decreases (see Figure 2–20B).
Cells use enzymes to catalyze the oxidation of organic molecules in small steps, through a sequence of reactions that allows useful energy to be harvested. We now need to explain how enzymes work and some of the constraints under which they operate.
Enzymes Lower the Activation-Energy Barriers That Block Chemical Reactions
Consider the reaction
paper + O2 → smoke + ashes + heat + CO2 + H2O
Once ignited, the paper burns readily, releasing to the atmosphere both energy as heat and water and carbon dioxide as gases. The reaction is irreversible, as the smoke and ashes never spontaneously retrieve these entities from the heated atmosphere and reconstitute themselves into paper. When the paper burns, its chemical energy is dissipated as heat—not lost from the universe, as energy can never be created or destroyed, but irretrievably dispersed in the chaotic random thermal motions of molecules. At the same time, the atoms and molecules of the paper become dispersed and disordered. In the language of thermodynamics, there has been a loss of free energy; that is, of energy that can be harnessed to do work or drive chemical reactions. This loss reflects a reduction of orderliness in the way the energy and molecules were stored in the paper.
We shall discuss free energy in more detail shortly, but the general principle is clear enough intuitively: chemical reactions proceed spontaneously only in the direction that leads to a loss of free energy. In other words, the spontaneous direction for any reaction is the direction that goes “downhill,” where a “downhill” reaction is one that is energetically favorable.
Although the most energetically favorable form of carbon under ordinary conditions is CO2, and that of hydrogen is H2O, a living organism does not disappear in a puff of smoke, and the paper book in your hands does not burst into flames. This is because the molecules both in the living organism and in the book are in a relatively stable state, and they cannot be changed to a state of lower energy without an input of energy; in other words, a molecule requires activation energy—a kick over an energy barrier—before it can undergo a chemical reaction that leaves it in a more stable state (Figure 2–21). In the case of a burning book, the activation energy can be provided by the heat of a lighted match. For the molecules in the watery solution inside a cell, the kick is delivered by an unusually energetic random collision with surrounding molecules.
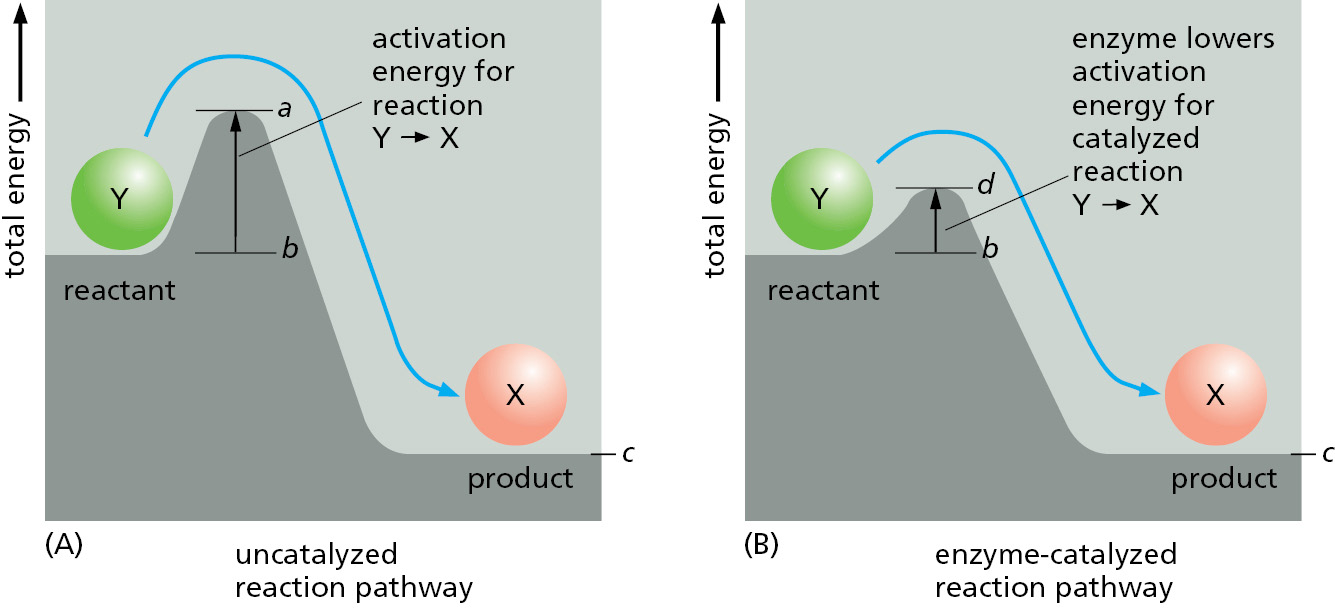
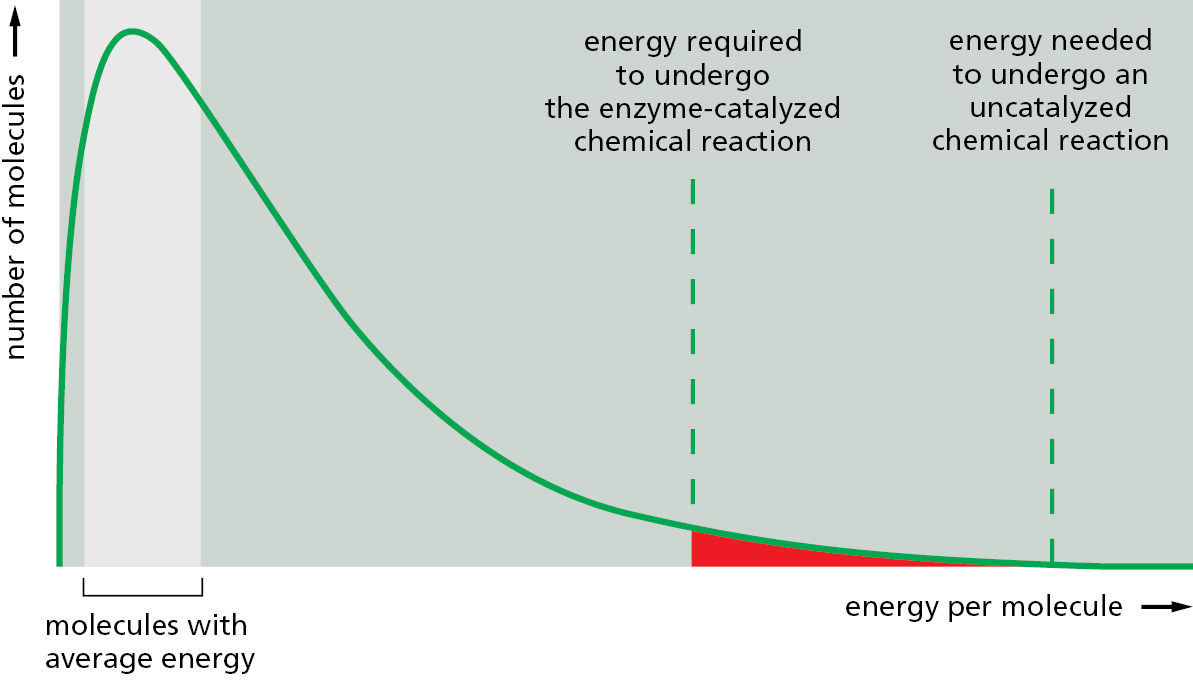
The chemistry in a living cell is tightly controlled, because the kick over energy barriers is greatly aided by a specialized class of proteins—the enzymes. Each enzyme binds tightly to one or more molecules, called substrates, and holds them in a way that greatly reduces the activation energy of a particular chemical reaction that the bound substrates can undergo. A substance that can lower the activation energy of a reaction is termed a catalyst; catalysts increase the rate of chemical reactions because they allow a much larger proportion of the random collisions with surrounding molecules to kick the substrates over the energy barrier, as illustrated in Figure 2–22. Enzymes are among the most effective catalysts known: some are capable of speeding up reactions by factors of 1014 or more. Enzymes thereby allow reactions that would not otherwise occur to proceed rapidly at normal temperatures.
Enzymes Can Drive Substrate Molecules Along Specific Reaction Pathways
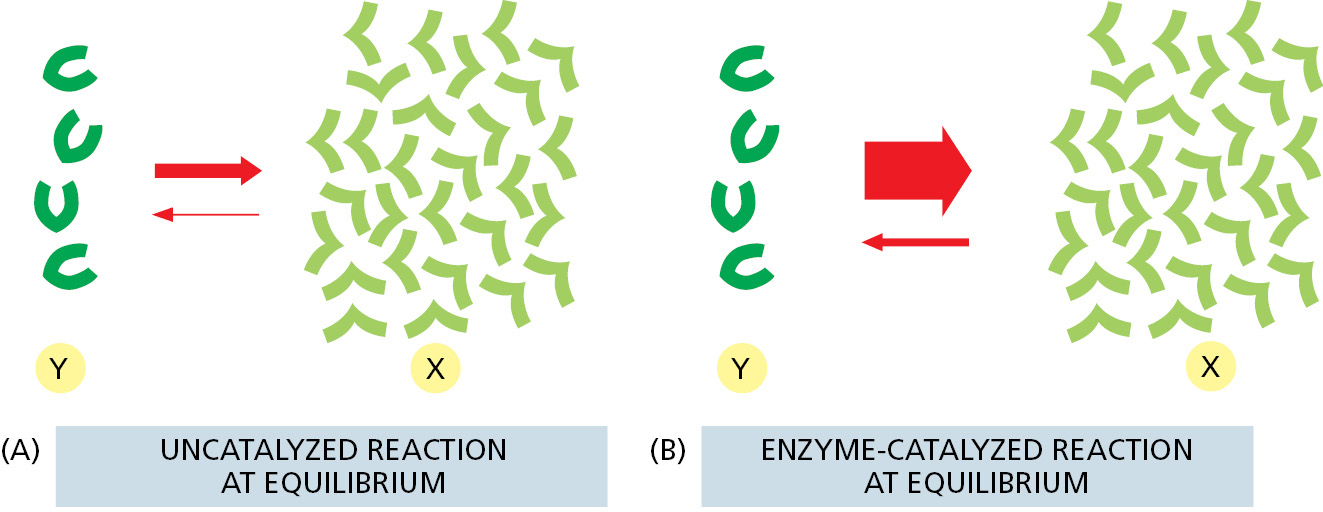
An enzyme cannot change the equilibrium point for a reaction. The reason is simple: when an enzyme (or any catalyst) lowers the activation energy for the reaction Y → X, of necessity it also lowers the activation energy for the reverse reaction X → Y by exactly the same amount (see Figure 2–21). The forward and backward reactions will therefore be accelerated by the same factor by an enzyme, and the equilibrium point for the reaction will be unchanged (Figure 2–23). Thus no matter how much an enzyme speeds up a reaction, it cannot change its direction.
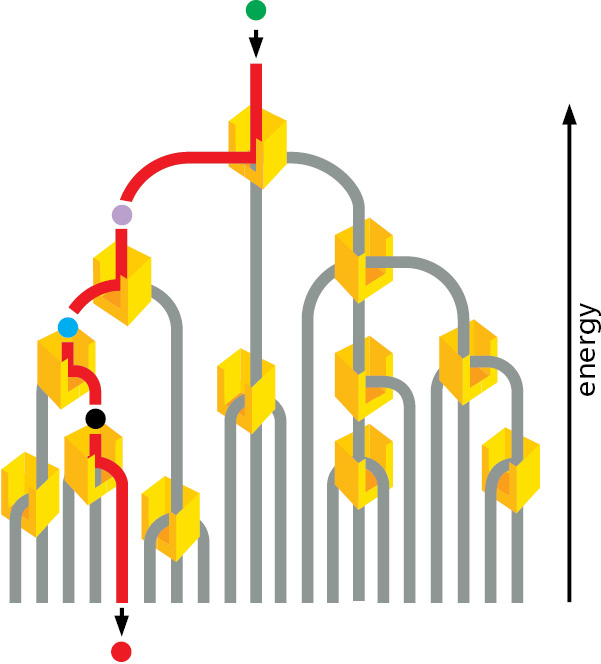
Despite the above limitation, enzymes steer all of the reactions in cells through specific reaction paths. This is because enzymes are both highly selective and very precise, usually catalyzing only one particular reaction. In other words, each enzyme selectively lowers the activation energy of only one of the several possible chemical reactions that its bound substrate molecules could undergo. In this way, sets of enzymes can direct each of the many different molecules in a cell along a particular reaction pathway (Figure 2–24).
The success of living organisms is attributable to a cell’s ability to make enzymes of many types, each with precisely specified properties. Each enzyme has a unique shape containing an active site, a pocket or groove in the enzyme into which only particular substrates will fit (Figure 2–25). Like all other catalysts, enzyme molecules themselves remain unchanged after participating in a reaction and therefore can function over and over again. In Chapter 3, we discuss further how enzymes work.
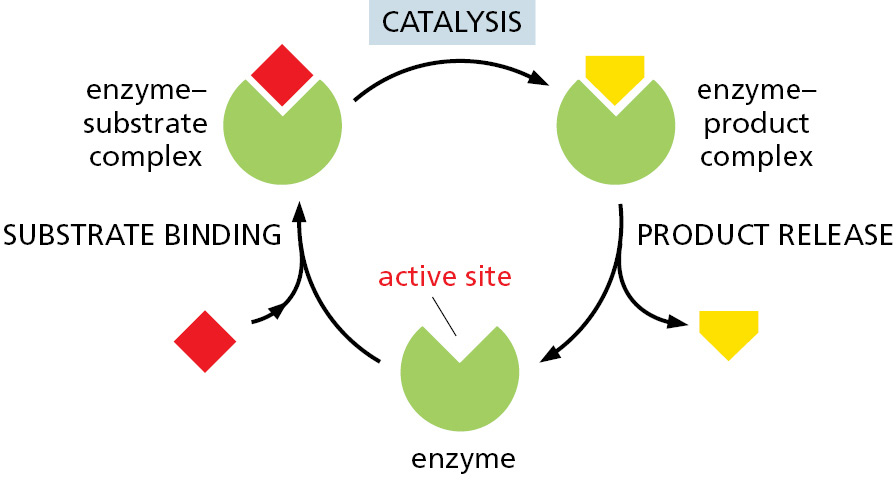
How Enzymes Find Their Substrates: The Enormous Rapidity of Molecular Motions
An enzyme will often catalyze the reaction of thousands of substrate molecules every second. This means the enzyme must be able to bind a new substrate molecule in a fraction of a millisecond. But both enzymes and their substrates are present in relatively small numbers in a cell. How do they find each other so fast? Rapid binding is possible because the motions caused by heat energy are enormously fast at the molecular level. These molecular motions can be classified broadly into three kinds: (1) the movement of a molecule from one place to another (translational motion), (2) the rapid back-and-forth movement of covalently linked atoms with respect to one another (vibrations), and (3) rotations. All three of these motions help to bring the surfaces of interacting molecules together.
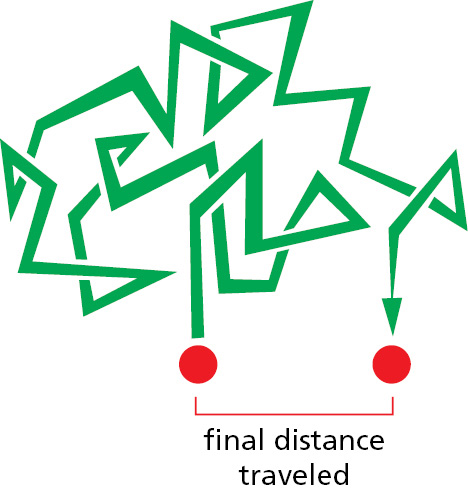
The rates of molecular motions can be measured by a variety of spectroscopic techniques. A large globular protein is constantly tumbling, rotating about its axis approximately a million times per second. Molecules are also in constant translational motion, which causes them to explore the space inside the cell very efficiently by wandering through it—a process called diffusion. In this way, every molecule in a cell collides with a huge number of other molecules each second. As the molecules in a liquid collide and bounce off one another, an individual molecule moves first one way and then another, its path constituting a random walk (Figure 2–26). In such a walk, the average net distance that each molecule travels (as the “crow flies”) from its starting point is proportional to the square root of the time involved; that is, if it takes a molecule 1 second on average to travel 1 μm, it takes 4 seconds to travel 2 μm, 100 seconds to travel 10 μm, and so on.
The inside of a cell is very crowded (Figure 2–27). Nevertheless, experiments in which fluorescent dyes and other labeled molecules are injected into cells show that small organic molecules diffuse through the watery gel of the cytosol nearly as rapidly as they do through water. A small organic molecule, for example, takes only about one-fifth of a second on average to diffuse a distance of 10 μm. Diffusion is therefore an efficient way for small molecules to move the limited distances in the cell (a typical animal cell is 15 μm in diameter).

Proteins also move rapidly in cells. But because enzymes move more slowly than substrates, we can think of them as sitting still. The rate of encounter of each enzyme molecule with its substrate will depend on the concentration of the substrate molecule. For example, some abundant substrates are present at a concentration of 0.5 mM. As pure water is 55.5 M, there is only about one such substrate molecule in the cell for every 105 water molecules. Nevertheless, the active site on an enzyme molecule that binds this substrate will be bombarded by about 500,000 random collisions with the substrate molecule per second. (For a substrate concentration tenfold lower, the number of collisions drops to 50,000 per second, and so on.) A random collision between the active site of an enzyme and the matching surface of its substrate molecule often leads immediately to the formation of an enzyme–substrate complex. A reaction in which a covalent bond is broken or formed can then occur extremely rapidly. When one appreciates how quickly molecules move and react, the observed rates of enzymatic catalysis do not seem so amazing.
Two molecules that are held together by noncovalent bonds can also dissociate. The multiple weak noncovalent bonds that they form with each other will persist until random thermal motion causes the two molecules to separate. In general, the stronger the binding of the enzyme and substrate, the slower their rate of dissociation. In contrast, whenever two colliding molecules have poorly matching surfaces, they form few noncovalent bonds and the total energy of association will be negligible compared with that of thermal motion. In this case, the two molecules dissociate as rapidly as they come together, preventing incorrect and unwanted associations between mismatched molecules, such as between an enzyme and the wrong substrate.
The Free-Energy Change for a Reaction, ΔG, Determines Whether It Can Occur Spontaneously
Although enzymes speed up reactions, they cannot by themselves force energetically unfavorable reactions to occur. In terms of a water analogy, enzymes by themselves cannot make water run uphill. Cells, however, must do just that in order to grow and divide: they must build highly ordered and energy-rich molecules from small and simple ones. We shall see that this is done through enzymes that directly couple energetically favorable reactions, which release energy and produce heat, to energetically unfavorable reactions, which produce biological order.
What do cell biologists mean by the term “energetically favorable,” and how can this be quantified? According to the second law of thermodynamics, the universe tends toward maximum disorder (largest entropy or greatest probability). Thus, a chemical reaction can proceed spontaneously only if it results in a net increase in the disorder of the universe (see Figure 2–16). This disorder of the universe can be expressed most conveniently in terms of the free energy of a system, a concept we touched on earlier.
Free energy, G, is an expression of the energy available to do work; for example, the work of driving chemical reactions. The value of G is of interest only when a system undergoes a change. The free-energy change, denoted ΔG (delta G), is critical because, as explained in Panel 2–7 (pp. 106–107), it is a direct measure of the amount of disorder created in the universe when a reaction takes place. Energetically favorable reactions, by definition, are those that decrease free energy; in other words, they have a negative ΔG and disorder the universe (Figure 2–28).

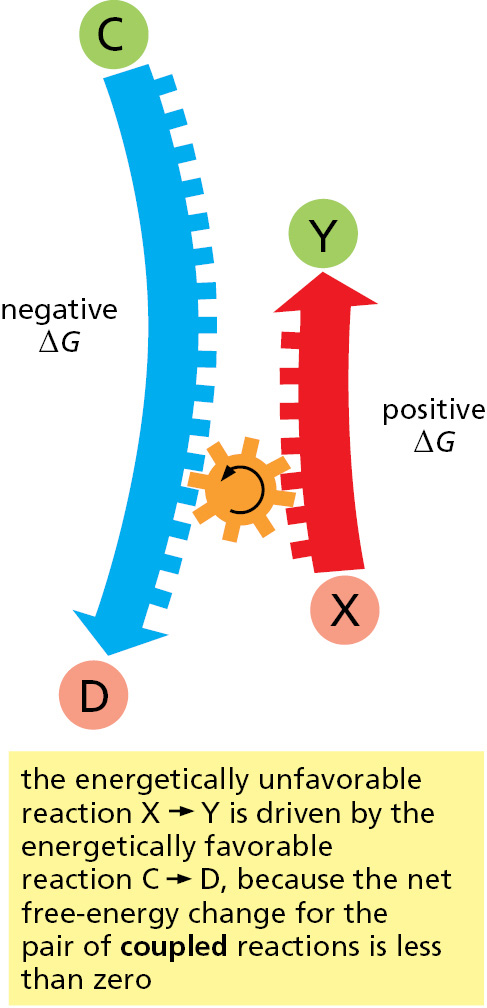
An example of an energetically favorable reaction on a macroscopic scale is the “reaction” by which a compressed spring relaxes to an expanded state, releasing its stored elastic energy as heat to its surroundings; an example on a microscopic scale is salt dissolving in water. Conversely, energetically unfavorable reactions with a positive ΔG—such as the joining of two amino acids to form a peptide bond—by themselves create order in the universe. Therefore, these reactions can take place only if they are coupled to a second reaction with a negative ΔG so large that the ΔG of the overall process is negative (Figure 2–29).
The Concentration of Reactants Influences the Free-Energy Change and a Reaction’s Direction
As we have just described, a reaction Y ↔ X will go in the direction Y → X when the associated free-energy change, ΔG, is negative, just as a tensed spring left to itself will relax and lose its stored energy to its surroundings as heat. For a chemical reaction, however, ΔG depends not only on the energy stored in each individual molecule but also on the concentrations of the molecules in the reaction mixture. Remember that ΔG reflects the degree to which a reaction creates a more disordered—in other words, a more probable—state of the universe. Recalling our coin analogy, it is very likely that a coin will flip from a head to a tail orientation if a jiggling box contains 90 heads and 10 tails, but this is a less probable event if the box has 10 heads and 90 tails.
The same is true for a chemical reaction. For a reversible reaction Y ↔ X, a large excess of Y over X will tend to drive the reaction in the direction Y → X. Therefore, as the ratio of Y to X increases, the ΔG becomes more negative for the transition Y → X (and more positive for the transition X → Y).
The amount of concentration difference that is needed to compensate for a given decrease in chemical-bond energy (and accompanying heat release) is not intuitively obvious. In the late nineteenth century, the relationship was determined through a thermodynamic analysis that makes it possible to separate the concentration-dependent and the concentration-independent parts of the free-energy change, as we describe next.
The Standard Free-Energy Change, ΔG°, Makes It Possible to Compare the Energetics of Different Reactions
Because ΔG depends on the concentrations of the molecules in the reaction mixture at any given time, it is not a particularly useful value for comparing the relative energies of different types of reactions. To consider reactions on a comparable basis, we need to turn to the standard free-energy change of a reaction, ΔG°. The ΔG° is the change in free energy under a standard condition, defined as that where the concentrations of all the reactants are set to the same fixed value of 1 mole/liter. Defined in this way, ΔG° depends only on the intrinsic characters of the reacting molecules.
For the simple reaction Y → X at 37°C, ΔG° is related to ΔG as follows:
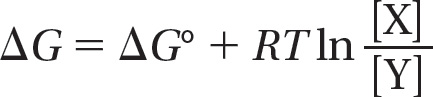
where ΔG is in kilojoules per mole, [Y] and [X] denote the concentrations of Y and X in moles/liter, ln is the natural logarithm, and RT is the product of the gas constant, R, and the absolute temperature, T. At 37°C, RT = 2.58 kJ mole–1. (A mole is 6 × 1023 molecules of a substance.)
A large body of thermodynamic data has been collected that has made it possible to determine the standard free-energy change, ΔG°, for the important metabolic reactions of a cell. Given these ΔG° values, combined with additional information about metabolite concentrations and reaction pathways, it is possible to quantitatively predict the course of most biological reactions.
The Equilibrium Constant and ΔG° Are Readily Derived from Each Other
Inspection of the above equation reveals that the ΔG equals the value of ΔG° when the concentrations of Y and X are equal. But as any favorable reaction proceeds, the concentrations of the products will increase as the concentration of the substrates decreases. This change in relative concentrations will cause [X]/[Y] to become increasingly large, making the initially favorable ΔG less and less negative (the logarithm of a number x is positive for x > 1, negative for x < 1, and zero for x = 1). Eventually, when ΔG = 0, a chemical equilibrium will be attained; here there is no net change in free energy to drive the reaction in either direction, inasmuch as the concentration effect just balances the push given to the reaction by ΔG°. As a result, the ratio of product to substrate reaches a constant value at chemical equilibrium (Figure 2–30).
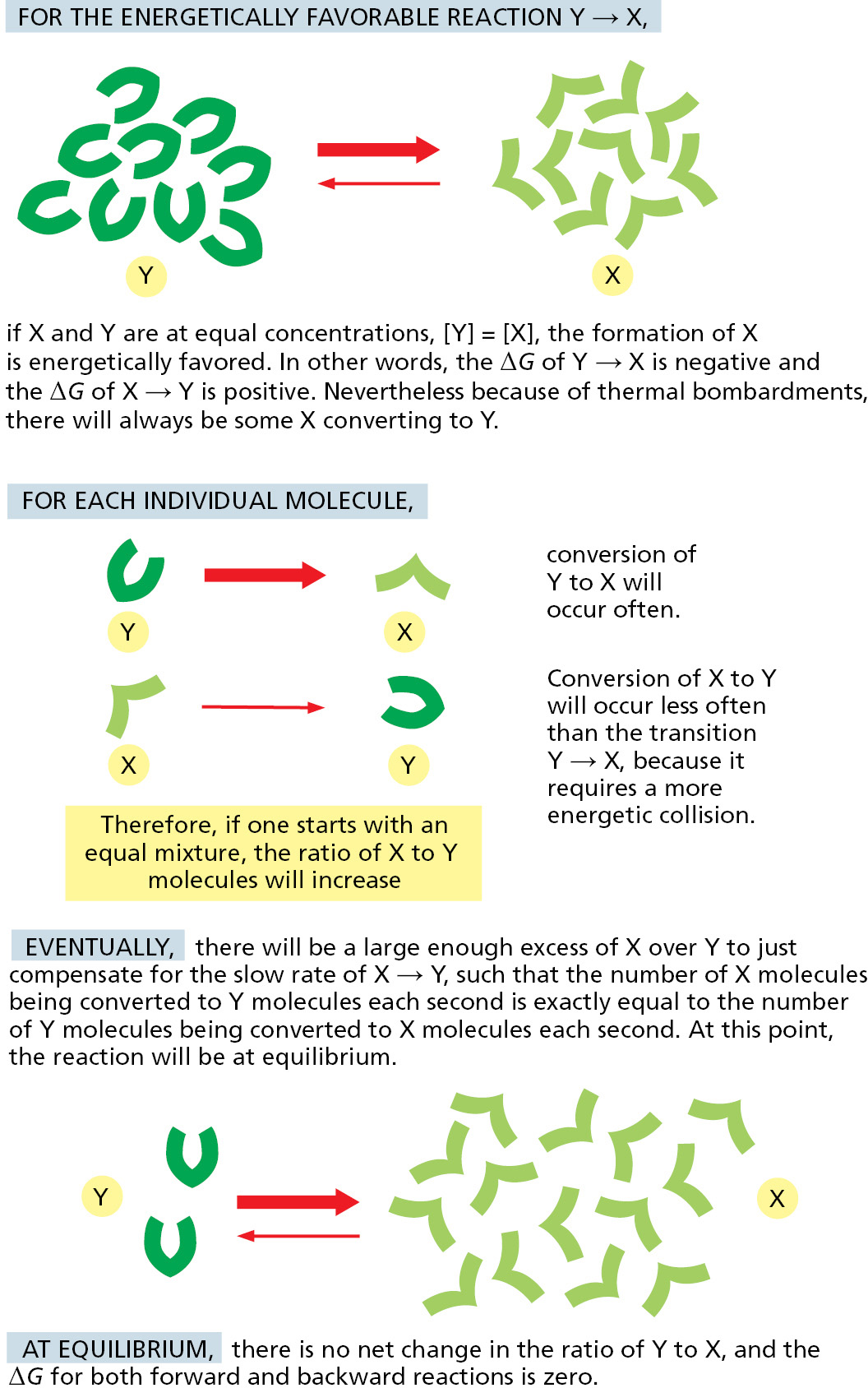
We can define the equilibrium constant, K, for the reaction Y → X as
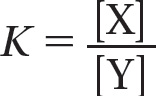
where [X] is the concentration of the product and [Y] is the concentration of the reactant at equilibrium. Remembering that ΔG = ΔG° + RT ln [X]/[Y], and that ΔG = 0 at equilibrium, we see that
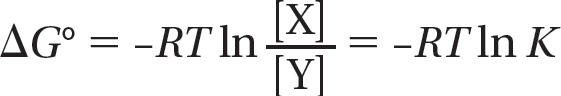
At 37°C, where RT = 2.58, the equilibrium equation is therefore:
ΔG° = –2.58 ln K
Converting this equation from the natural logarithm (ln) to the more commonly used base 10 logarithm (log), we get
ΔG° = –5.94 log K
The above equation reveals how the equilibrium ratio of X to Y (expressed as the equilibrium constant, K) depends on the intrinsic character of the molecules (as expressed in the value of ΔG° in kilojoules per mole). The more energetically favorable a reaction, the more product will accumulate when the reaction proceeds to equilibrium. More precisely, for every 5.94 kJ/mole difference in free energy at 37°C, the equilibrium constant changes by a factor of 10 (Table 2–2). Note that this amount of free-energy difference is roughly equivalent to the free energy available from a single hydrogen bond.
More generally, for a reaction that has multiple reactants and products, such as A + B → C + D,
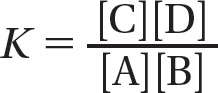
The concentrations of the two reactants and the two products are multiplied because the rate of the forward reaction depends on the collision of A and B and the rate of the backward reaction depends on the collision of C and D. Thus, at 37°C,
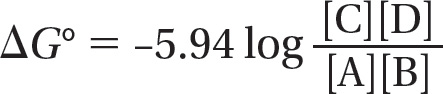
where ΔG° is in kilojoules per mole, and [A], [B], [C], and [D] denote the concentrations of the reactants and products in moles/liter.
The Free-Energy Changes of Coupled Reactions Are Additive
We have pointed out that unfavorable reactions can be coupled to favorable ones to drive the unfavorable ones forward (see Figure 2–29). In thermodynamic terms, this is possible because the overall free-energy change for a set of coupled reactions is the sum of the free-energy changes in each of its component steps. Consider, as a simple example, two sequential reactions
X → Y and Y → Z
whose ΔG° values are +5 and –13 kJ/mole, respectively. If these two reactions occur sequentially, the ΔG° for the coupled reaction will be –8 kJ/mole. This means that, with appropriate conditions, the unfavorable reaction X → Y can be driven by the favorable reaction Y → Z, provided that this second reaction follows the first. For example, several of the reactions in the long pathway that converts sugars into CO2 and H2O have positive ΔG° values. But the pathway nevertheless proceeds because the total ΔG° for the series of sequential reactions has a large negative value.
Forming a sequential pathway is not adequate for many purposes. Often the desired pathway is simply X → Y, without further conversion of Y to some other product. Fortunately, there are other more general ways of using enzymes to couple reactions together. In order to explain how this is possible, we need to introduce the activated carrier molecules that we discuss next.
Activated Carrier Molecules Are Essential for Biosynthesis
To make life possible, the energy released by the oxidation of food molecules must be stored temporarily before it can be channeled into the construction of the many other molecules needed by the cell. In most cases, the energy is stored as chemical-bond energy in a small set of activated “carrier molecules,” which contain one or more energy-rich covalent bonds. These molecules diffuse rapidly throughout the cell and thereby carry their bond energy from sites of energy generation to the sites where the energy will be used for biosynthesis and other cell activities (Figure 2–31).
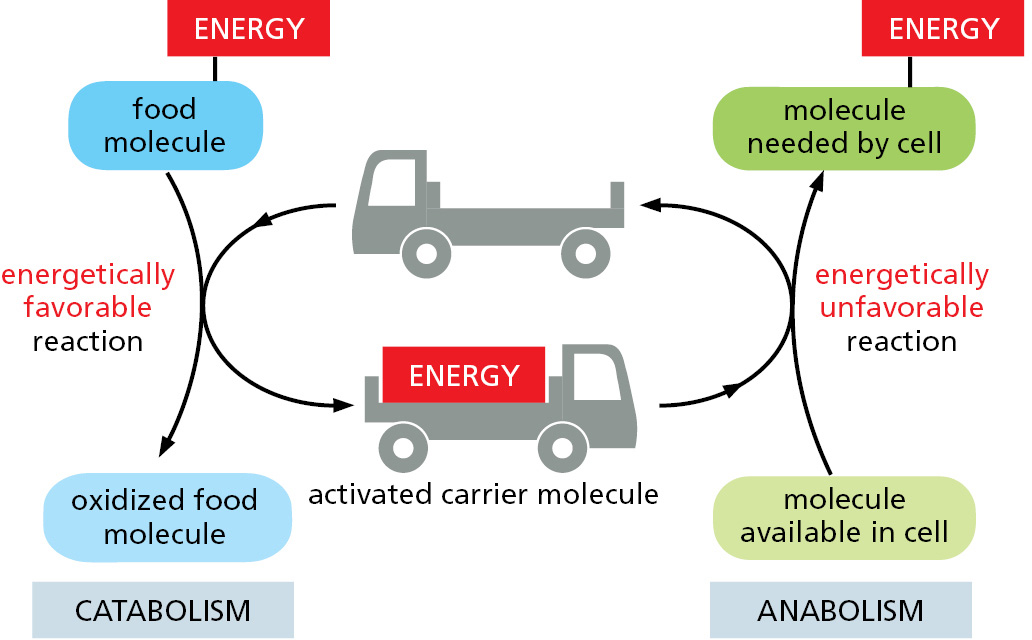
The activated carriers store energy in an easily exchangeable form, either as a readily transferable chemical group or as electrons held at a high energy level, and they can serve a dual role as a source of both energy and chemical groups in biosynthetic reactions. For historical reasons, these molecules are also sometimes referred to as coenzymes. The most important of the activated carrier molecules are ATP and two molecules that are closely related to each other, NADH and NADPH. As we discuss next, coupled reactions allow cells both to generate such activated carrier molecules and to use them like money to pay for reactions that otherwise could not take place.
The Formation of an Activated Carrier Is Coupled to an Energetically Favorable Reaction
Coupling mechanisms require enzymes and are fundamental to all the energy transactions of the cell. The nature of a coupled reaction is illustrated by a mechanical analogy in Figure 2–32, in which an energetically favorable chemical reaction is represented by rocks falling from a cliff. The energy of falling rocks would normally be entirely wasted in the form of heat generated by friction when the rocks hit the ground (see the falling-brick diagram in Figure 2–17). By careful design, however, part of this energy could be used instead to drive a paddle wheel that lifts a bucket of water (Figure 2–32B). Because the rocks can now reach the ground only after moving the paddle wheel, we say that the energetically favorable reaction of rock falling has been directly coupled to the energetically unfavorable reaction of lifting the bucket of water. Note that because part of the energy is used to do work in Figure 2–32B, the rocks hit the ground with less velocity than in Figure 2–32A, and correspondingly less energy is dissipated as heat.
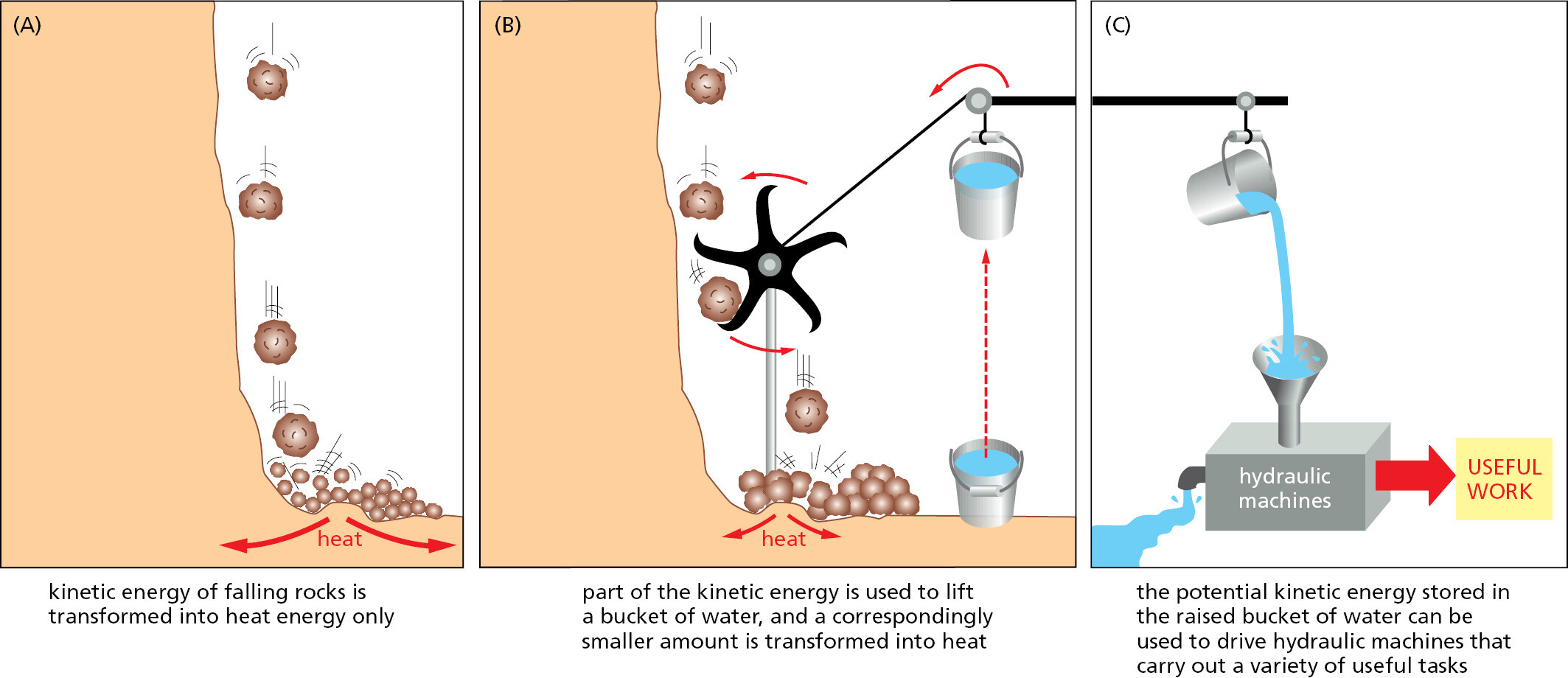
Similar processes occur in cells, where enzymes play the role of the paddle wheel. By mechanisms that we discuss later in this chapter, enzymes couple an energetically favorable reaction, such as the oxidation of foodstuffs, to an energetically unfavorable reaction, such as the generation of an activated carrier molecule. As in this example, the amount of heat released by the oxidation reaction is reduced by exactly the amount of energy stored in the energy-rich covalent bonds of the activated carrier molecule. And the activated carrier molecule picks up a packet of energy of a size sufficient to power a chemical reaction elsewhere in the cell.
ATP Is the Most Widely Used Activated Carrier Molecule
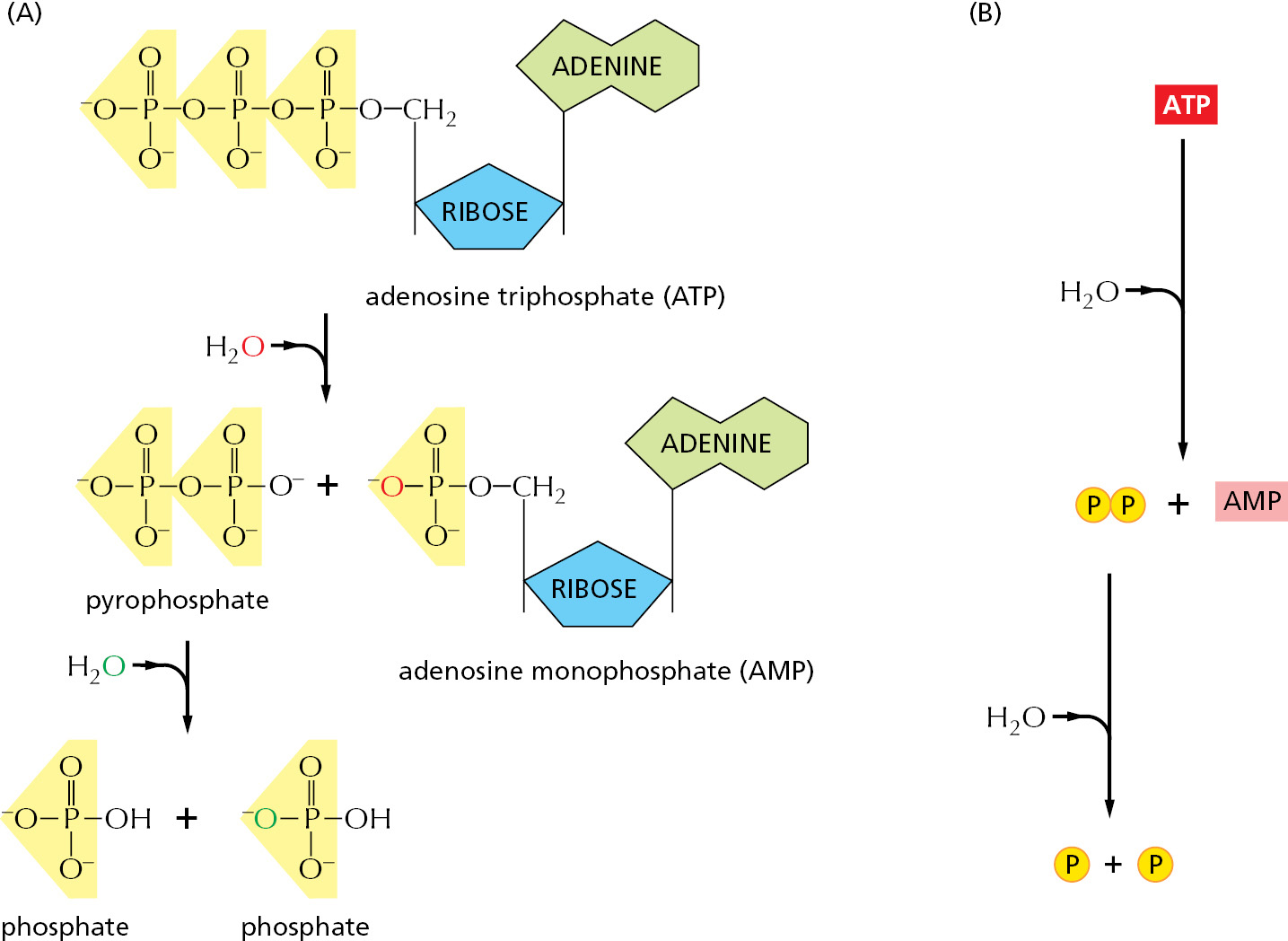
The most important and versatile of the activated carriers in cells is ATP (adenosine triphosphate). Just as the energy stored in the raised bucket of water in Figure 2–32B can drive a wide variety of hydraulic machines, ATP is a convenient and versatile store, or currency, of energy used to drive a huge variety of chemical reactions in cells. ATP is synthesized by coupling a reaction that is highly energetically favorable to an energetically unfavorable phosphorylation reaction in which a phosphate group is added to ADP (adenosine diphosphate). When required, ATP gives up its energy packet through its energetically favorable hydrolysis to ADP and inorganic phosphate (Figure 2–33). The regenerated ADP is then available to be used for another round of the phosphorylation reaction that forms ATP.
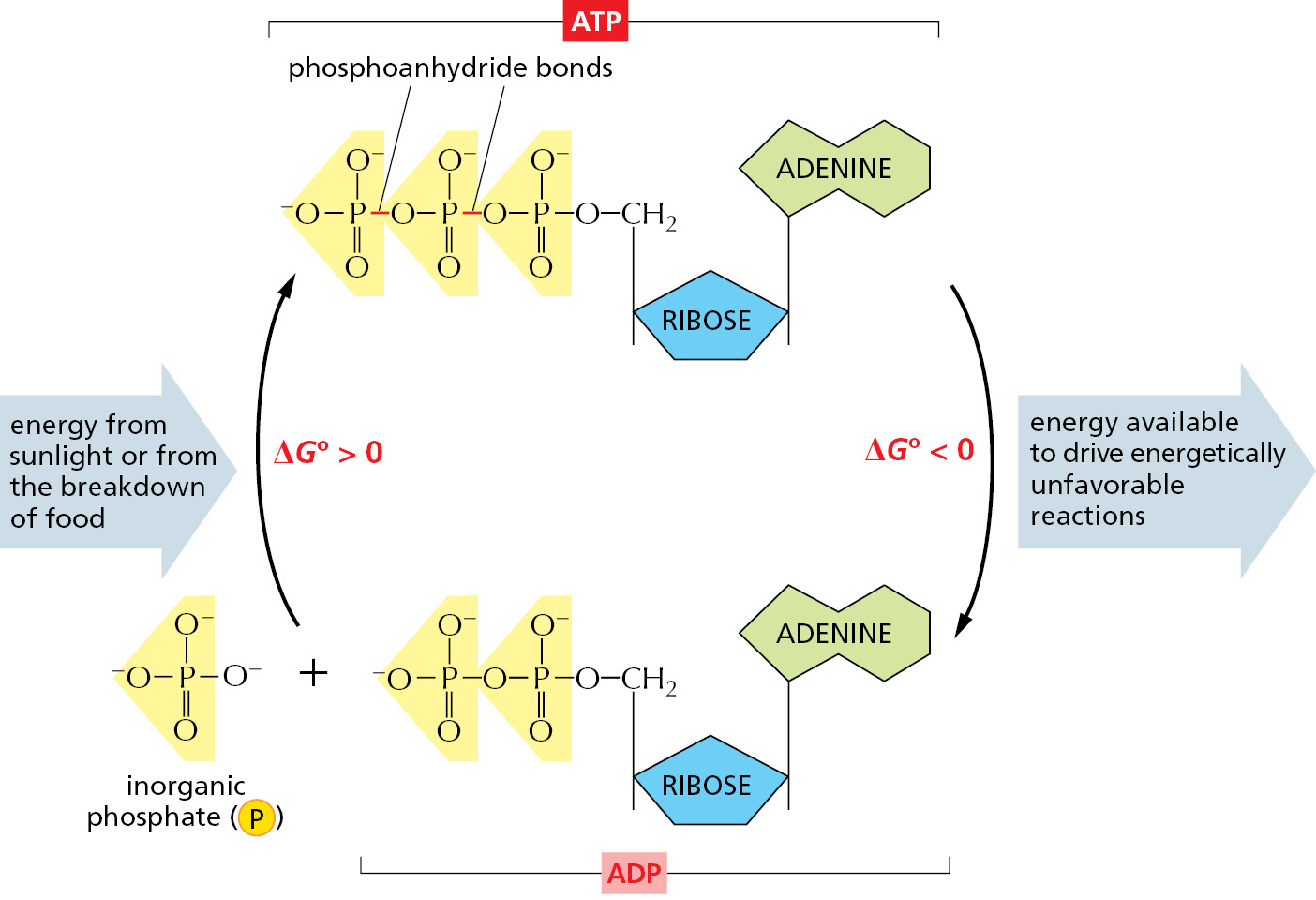
The formation of ATP from ADP and phosphate reverses the hydrolysis reaction; because this condensation reaction is energetically unfavorable, it must be coupled to a highly energetically favorable reaction to occur.
The two outermost phosphate groups in ATP are said to be held to the rest of the molecule by “high-energy” covalent bonds, because each of these phosphoanhydride linkages releases a great deal of free energy when hydrolyzed. The unusually large negative free-energy change for these hydrolysis reactions arises from a number of factors. The release of the terminal phosphate group when ATP forms ADP removes an unfavorable repulsion between adjacent negative charges; in addition, the inorganic phosphate ion released is stabilized both by resonance and by favorable hydrogen-bond formation with water.
The energetically favorable reaction of ATP hydrolysis is coupled to many otherwise unfavorable reactions through which needed molecules are synthesized. Many of these coupled reactions involve the transfer of the terminal phosphate in ATP to another molecule, as illustrated by the phosphorylation reaction in Figure 2–34.
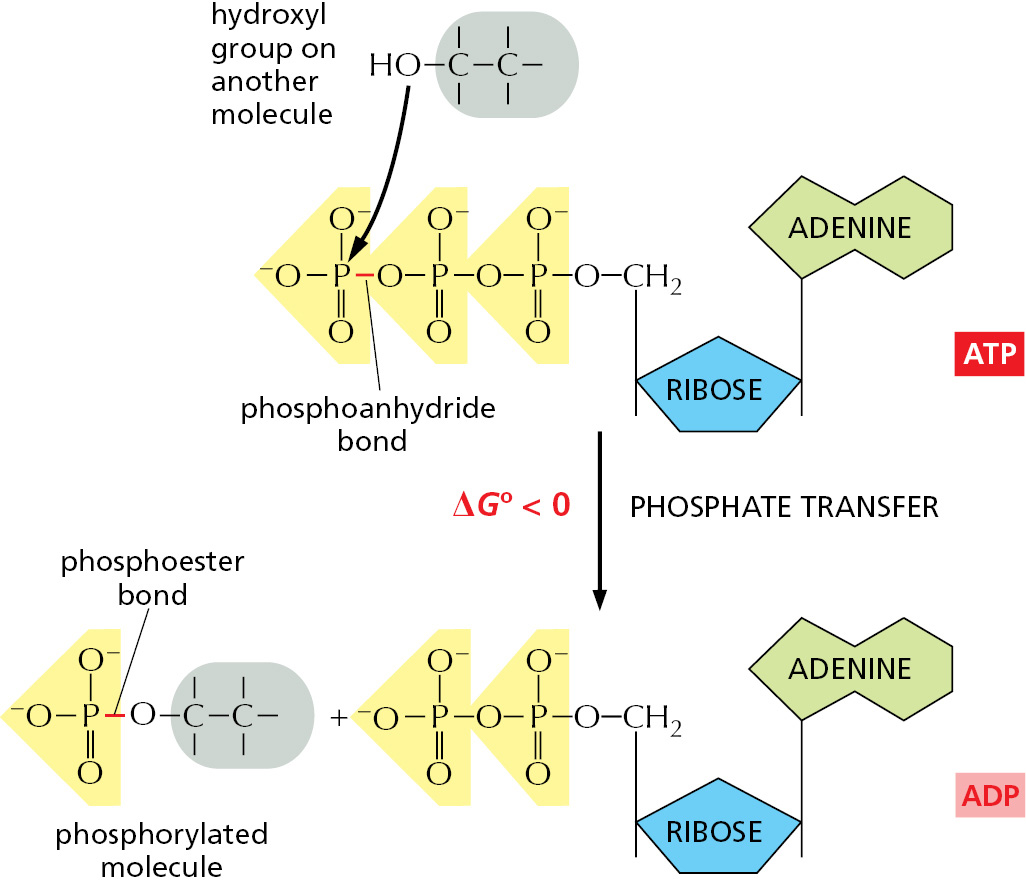
As the most abundant activated carrier in cells, ATP is the principal energy currency. To give just two examples, it supplies energy for many of the pumps that transport substances into and out of the cell (discussed in Chapter 11), and it powers the molecular motors that enable muscle cells to contract and nerve cells to transport materials from one end of their long axons to another (discussed in Chapter 16).
Energy Stored in ATP Is Often Harnessed to Join Two Molecules Together
We have previously discussed one way in which an energetically favorable reaction can be coupled to an energetically unfavorable reaction, X → Y, so as to enable it to occur. In that scheme, a second enzyme catalyzes the energetically favorable reaction Y → Z, pulling all of the X to Y in the process. But when the required product is Y and not Z, this mechanism is not useful.
A typical biosynthetic reaction is one in which two molecules, A and B, are joined together to produce A–B in the energetically unfavorable condensation reaction
B–H + A–OH → A–B + H2O
There is an indirect pathway that allows B–H and A–OH to form A–B, in which a coupling to ATP hydrolysis makes the reaction go. Here, energy from ATP hydrolysis is first used to convert A–OH to a higher-energy intermediate compound, which then reacts directly with B–H to give A–B. The simplest possible mechanism involves the transfer of a phosphate from ATP to A–OH to make A–O–PO3, in which case the reaction pathway contains only two steps:
- A–OH + ATP → A–O–PO3 + ADP
- B–H + A–O–PO3 → A–B + phosphate
Net result: A–OH + ATP + B–H → A–B + ADP + phosphate
The condensation reaction, which by itself is energetically unfavorable, is forced to occur by being directly coupled to ATP hydrolysis in an enzyme-catalyzed reaction pathway (Figure 2–35A).
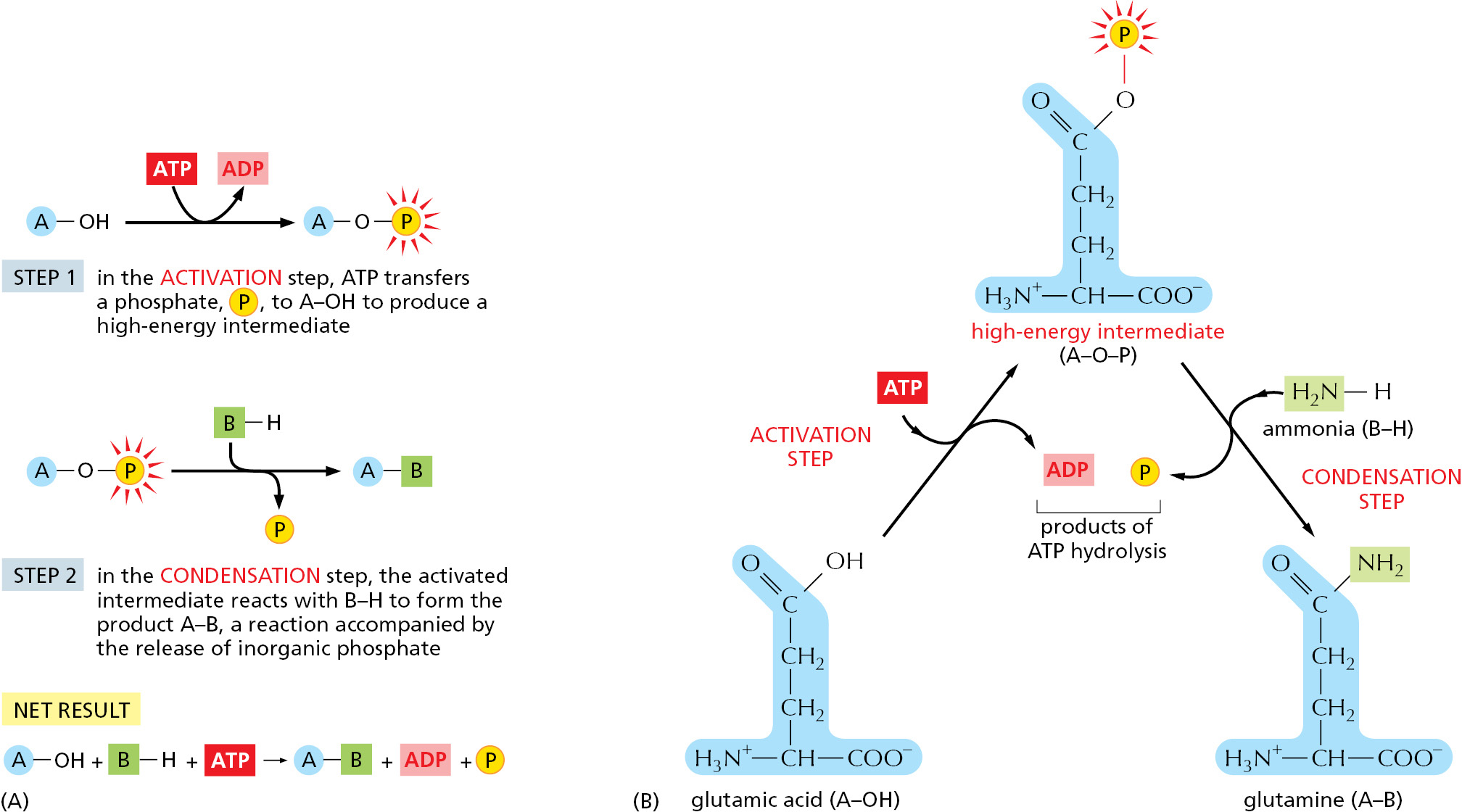
A biosynthetic reaction of exactly this type synthesizes the amino acid glutamine (Figure 2–35B). We will see shortly that similar (but more complex) mechanisms are also used to produce nearly all of the large molecules of the cell.
NADH and NADPH Are Important Electron Carriers
Other important activated carrier molecules participate in oxidation–reduction reactions and are commonly part of coupled reactions in cells. These activated carriers are specialized to carry electrons held at a high energy level (sometimes called “high-energy” electrons) and hydrogen atoms. The most important of these electron carriers are NAD+ (nicotinamide adenine dinucleotide) and the closely related molecule NADP+ (nicotinamide adenine dinucleotide phosphate). As part of an enzyme-catalyzed reaction in which a substrate molecule is oxidized, each picks up a “packet of energy” corresponding to two electrons plus a proton (H+), and they are thereby converted to NADH (reduced nicotinamide adenine dinucleotide) and NADPH (reduced nicotinamide adenine dinucleotide phosphate), respectively (Figure 2–36). These molecules can therefore be regarded as carriers of hydride ions (the H+ plus two electrons, or H–).
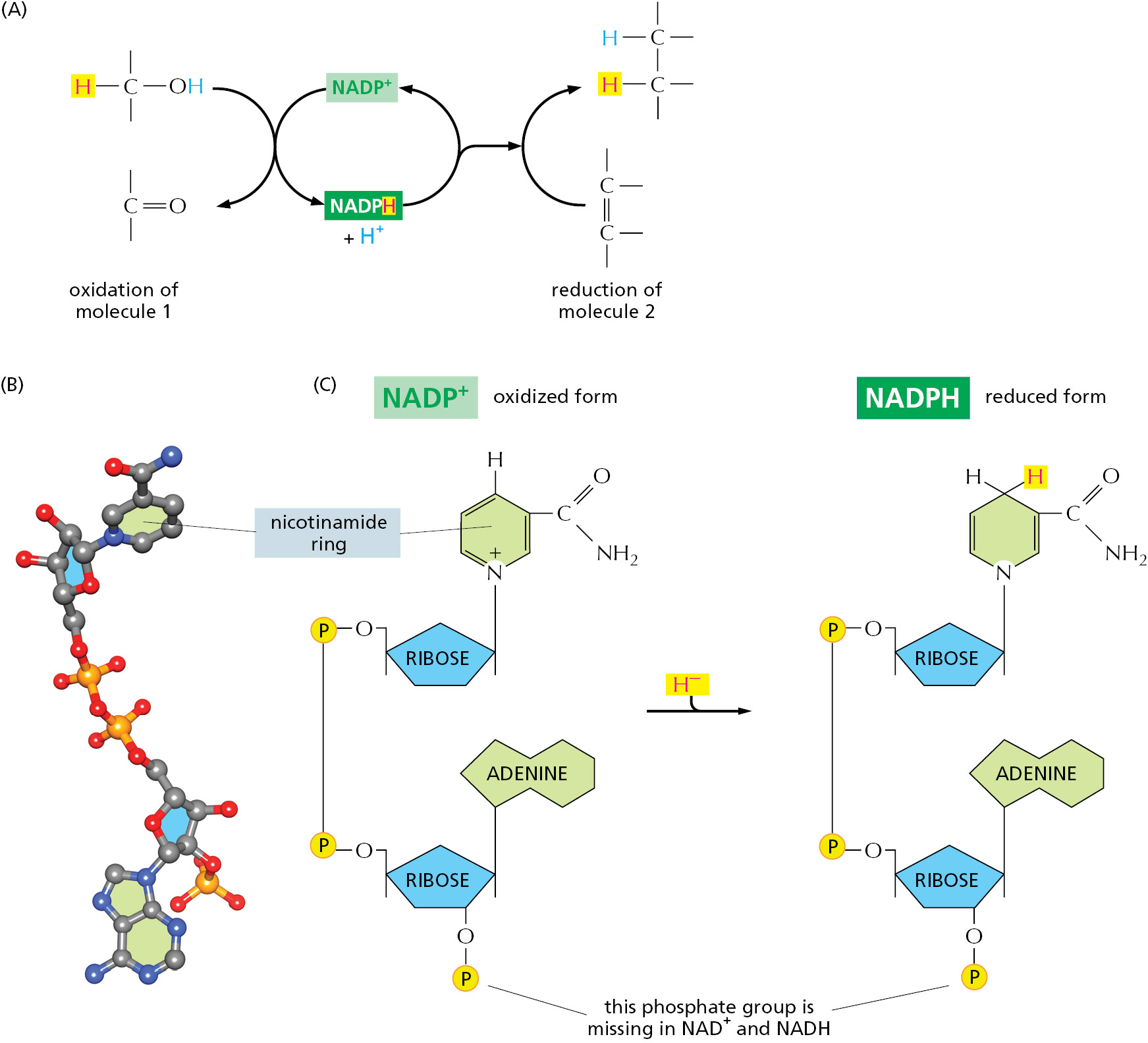
Like ATP, NADPH is an activated carrier that participates in many important biosynthetic reactions that would otherwise be energetically unfavorable. The NADPH is produced according to the general scheme shown in Figure 2–36A. During a special set of energy-yielding catabolic reactions, two hydrogen atoms are removed from a substrate molecule. Both electrons but just one hydrogen atom (that is, a hydride ion, H–) are added to the nicotinamide ring of NADP+ to form NADPH; the second hydrogen atom is released as a proton (H+) into solution. This is a typical oxidation–reduction reaction, in which the substrate is oxidized and NADP+ is reduced.
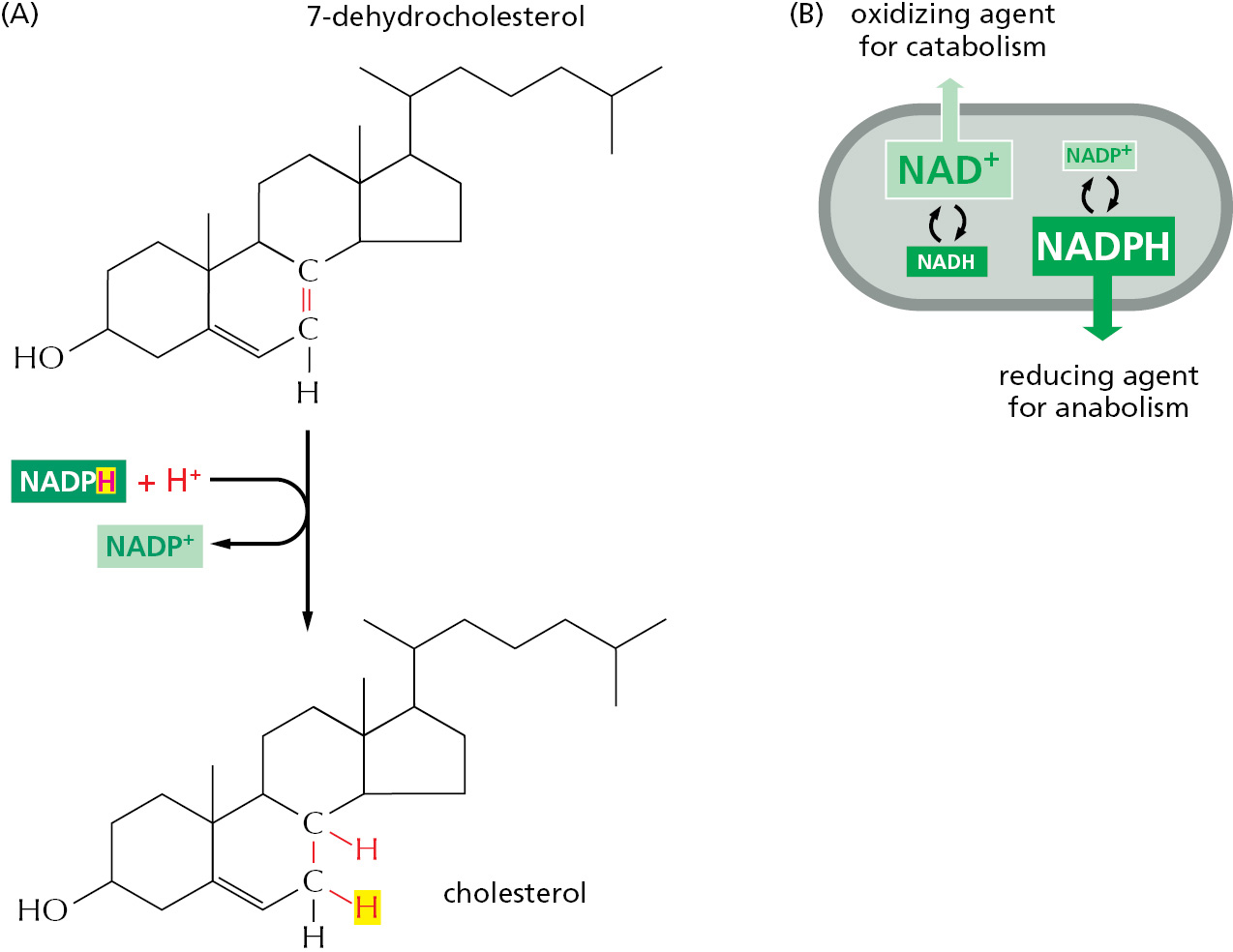
NADPH readily gives up the hydride ion it carries in a subsequent oxidation–reduction reaction, because the nicotinamide ring can achieve a more stable arrangement of electrons without it. In this subsequent reaction, which regenerates NADP+, it is the NADPH that is oxidized and the substrate that is reduced. The NADPH is an effective donor of its hydride ion to other molecules for the same reason that ATP readily transfers a phosphate: in both cases the transfer is accompanied by a large negative free-energy change. One example of the use of NADPH in biosynthesis is shown in Figure 2–37.
The extra phosphate group on NADPH has no effect on the electron-transfer properties of NADPH compared with NADH, being far away from the region involved in electron transfer (see Figure 2–36C). It does, however, give a molecule of NADPH a slightly different shape from that of NADH, making it possible for NADPH and NADH to bind as substrates to completely different sets of enzymes. Thus, the two types of carriers are used to transfer electrons (or hydride ions) between two different sets of molecules.
Why should there be this division of labor? The answer lies in the need to regulate two sets of electron-transfer reactions independently. NADPH operates chiefly with enzymes that catalyze anabolic reactions, supplying the high-energy electrons needed to synthesize energy-rich biological molecules. NADH, by contrast, has a special role as an intermediate in the catabolic system of reactions that generate ATP through the oxidation of food molecules, as we will discuss shortly. The geneses of NADH from NAD+ and of NADPH from NADP+ occur by different pathways and are independently regulated so that the cell can adjust the supply of electrons for these two contrasting purposes. Inside the cell the ratio of NAD+ to NADH is kept high, whereas the ratio of NADP+ to NADPH is kept low. This provides plenty of NAD+ to act as an oxidizing agent and plenty of NADPH to act as a reducing agent (Figure 2–37B)—as required for their special roles in catabolism and anabolism, respectively.
There Are Many Other Activated Carrier Molecules in Cells
Other activated carriers also pick up and carry a chemical group in an easily transferred, high-energy linkage. For example, coenzyme A carries a readily transferable acetyl group in a thioester linkage and in this activated form is known as acetyl CoA (acetyl coenzyme A). Acetyl CoA (Figure 2–38) is used to add two carbon units in the biosynthesis of larger molecules.
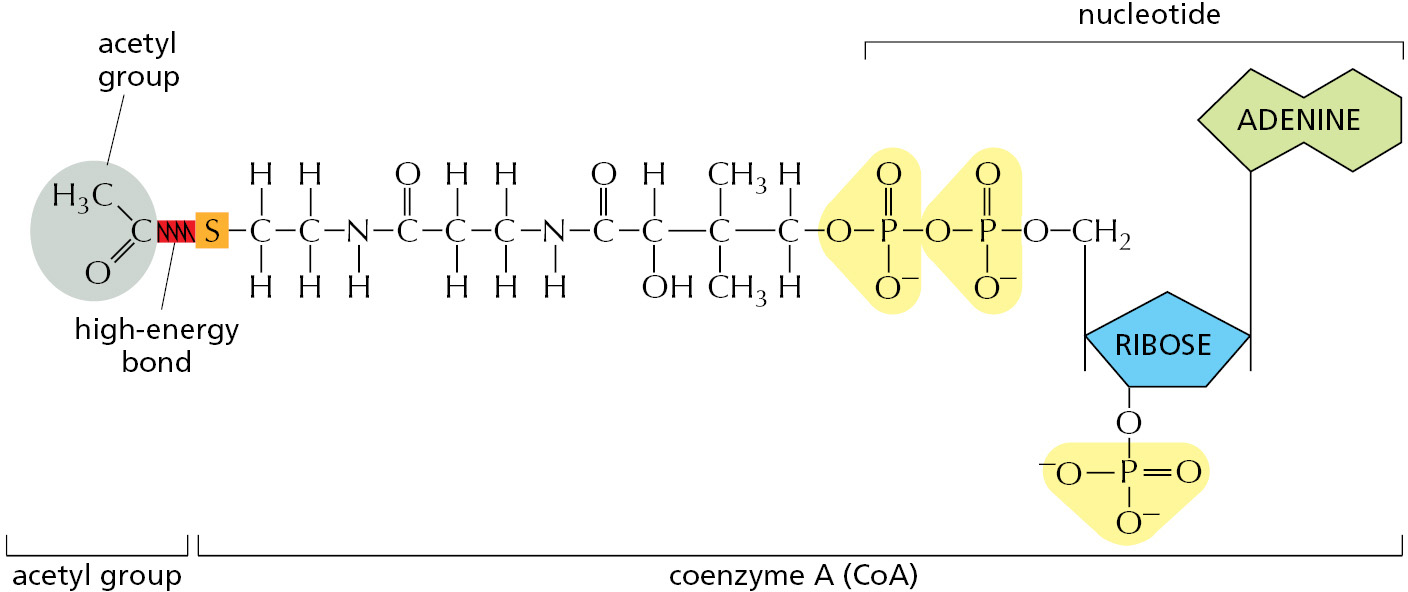
In acetyl CoA, as in other carrier molecules, the transferable group makes up only a small part of the molecule. The rest consists of a large organic portion that serves as a convenient “handle,” facilitating the recognition of the carrier molecule by specific enzymes. As with acetyl CoA, this handle portion very often contains a nucleotide derivative (usually adenosine diphosphate), a curious fact that may be a relic from an early stage of evolution. It is currently thought that the main catalysts for early life-forms—before DNA or proteins—were RNA molecules (or their close relatives), as described in Chapter 6. It is tempting to speculate that many of the carrier molecules that we find today originated in this earlier RNA world, where their nucleotide portions could have been useful for binding them to RNA enzymes (ribozymes).
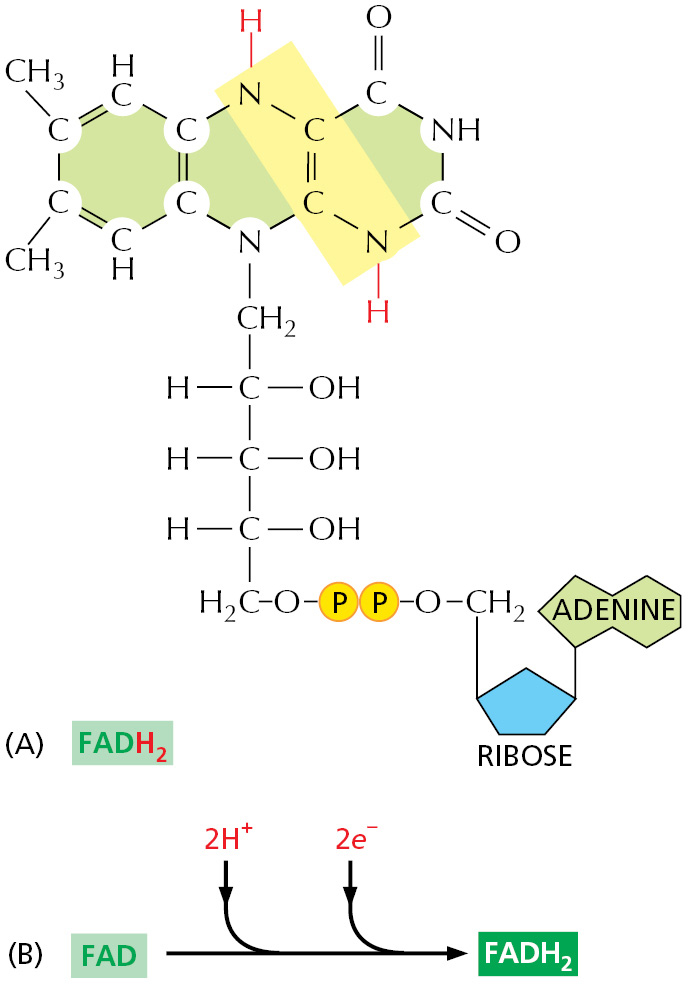
Thus, ATP transfers phosphate, NADPH transfers electrons and hydrogen, and acetyl CoA transfers two-carbon acetyl groups. FADH2 (reduced flavin adenine dinucleotide) is used like NADH in electron and proton transfers (Figure 2–39). The reactions of other activated carrier molecules involve the transfer of a methyl, carboxyl, or glucose group for biosyntheses (Table 2–3). These activated carriers are generated in reactions that are coupled to ATP hydrolysis, as in the example in Figure 2–40. Therefore, the energy that enables their groups to be used for biosynthesis ultimately comes from the catabolic reactions that generate ATP. Similar processes occur in the synthesis of the very large molecules of the cell—the nucleic acids, proteins, and polysaccharides—that we discuss next.
|
TABLE 2–3 Some Activated Carrier Molecules Widely Used in Metabolism |
|
|
Activated carrier |
Group carried in high-energy linkage |
|
ATP |
Phosphate |
|
NADH, NADPH, FADH2 |
Electrons and hydrogens |
|
Acetyl CoA |
Acetyl group |
|
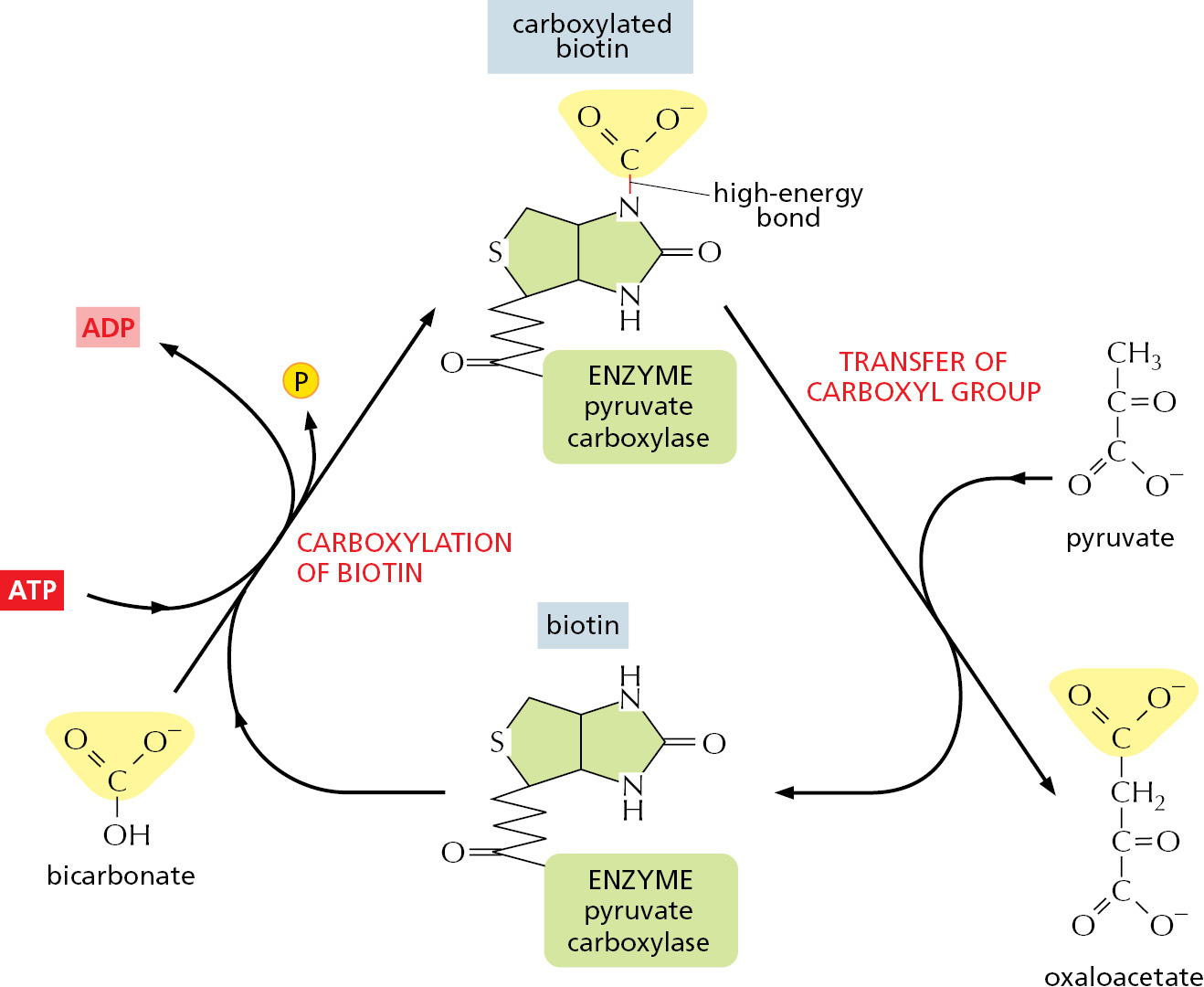
Carboxylated biotin |
Carboxyl group |
|
S-Adenosylmethionine |
Methyl group |
|
Uridine diphosphate glucose |
Glucose |
The Synthesis of Biological Polymers Is Driven by ATP Hydrolysis
As discussed previously, the macromolecules of the cell constitute most of its dry mass (see Figure 2–7). These molecules are made from subunits (or monomers) that are linked together in a condensation reaction, in which the constituents of a water molecule (OH plus H) are removed from the two reactants. Consequently, the reverse reaction—the breakdown of all three types of polymers—occurs by the enzyme-catalyzed addition of water (hydrolysis). This hydrolysis reaction is energetically favorable, whereas the biosynthetic reactions require an energy input (see Figure 2–9).
The nucleic acids (DNA and RNA), proteins, and polysaccharides are all polymers that are produced by the repeated addition of a monomer onto one end of a growing chain. The synthesis reactions for these three types of macromolecules are outlined in Figure 2–41. As indicated, the condensation step in each case depends on energy from nucleoside triphosphate hydrolysis. And yet, except for the nucleic acids, there are no phosphate groups left in the final product molecules. How are the reactions that release the energy of ATP hydrolysis coupled to polymer synthesis?
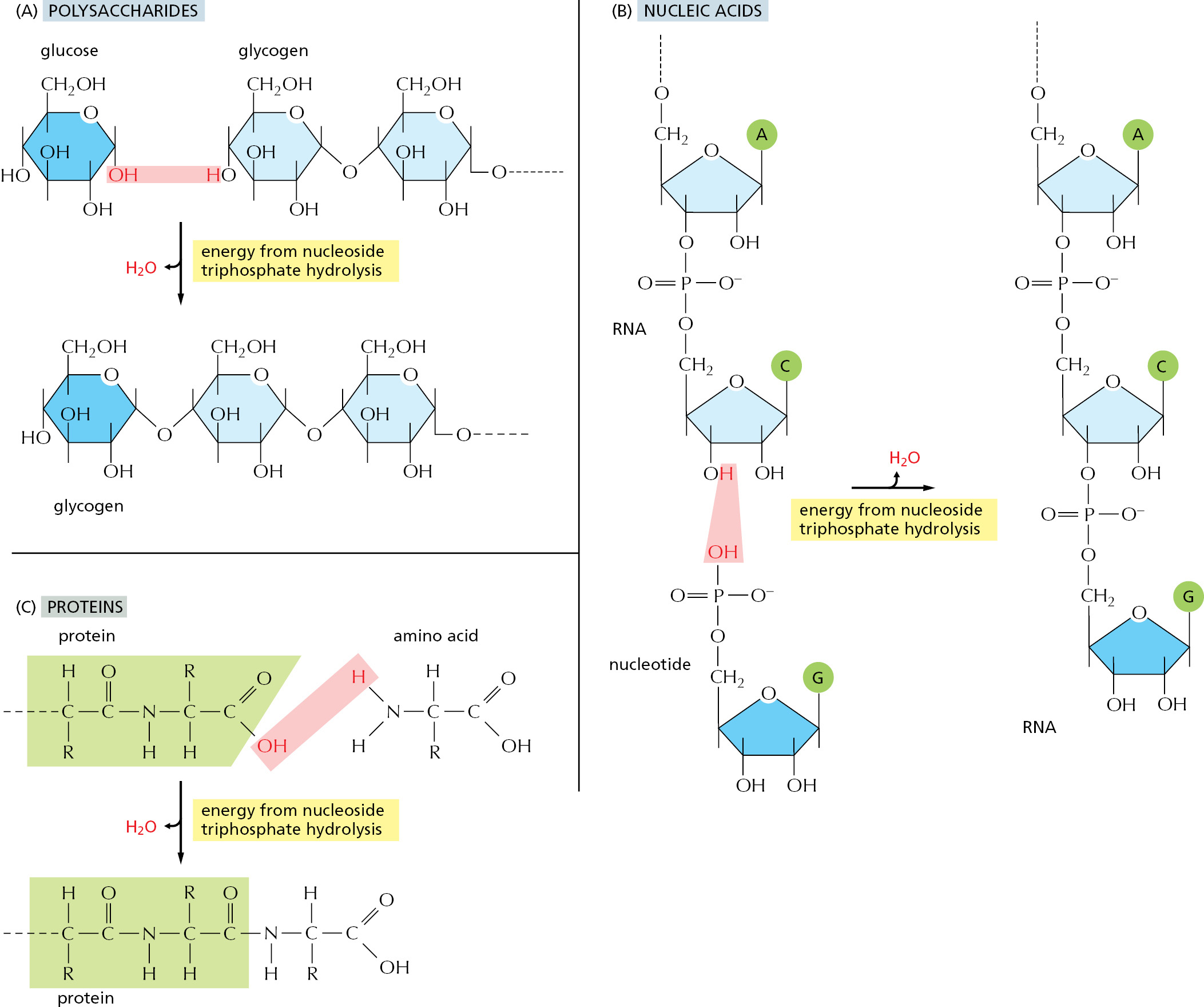
For each type of macromolecule, an enzyme-catalyzed pathway exists, which resembles that discussed previously for the synthesis of the amino acid glutamine (see Figure 2–35). The principle is exactly the same, in that the –OH group that will be removed in the condensation reaction is first activated by becoming involved in a high-energy linkage to a second molecule. However, the actual mechanisms used to link ATP hydrolysis to the synthesis of proteins and polysaccharides are more complex than that used for glutamine synthesis, inasmuch as more than one high-energy intermediate is required to generate the final high-energy bond that is broken during the condensation step (discussed in Chapter 6 for protein synthesis).
Each activated carrier has limits in its ability to drive a biosynthetic reaction. The ΔG for the hydrolysis of ATP to ADP and phosphate depends on the concentrations of all of the reactants, but under the usual conditions in a cell it is between –46 and –54 kJ/mole. In principle, this hydrolysis reaction could drive an unfavorable reaction with a ΔG of, perhaps, +40 kJ/mole, provided that a suitable reaction path is available. For some biosynthetic reactions, however, even –50 kJ/mole does not provide enough of a driving force. In these cases, the path of ATP hydrolysis can be altered so that it initially produces AMP and pyrophosphate, which is itself then hydrolyzed in a subsequent step (Figure 2–42). The whole process makes available a total free-energy change of about –100 kJ/mole. An important type of biosynthetic reaction that is driven in this way is the synthesis of nucleic acids (polynucleotides) from nucleoside triphosphates, as illustrated on the right side of Figure 2–43.
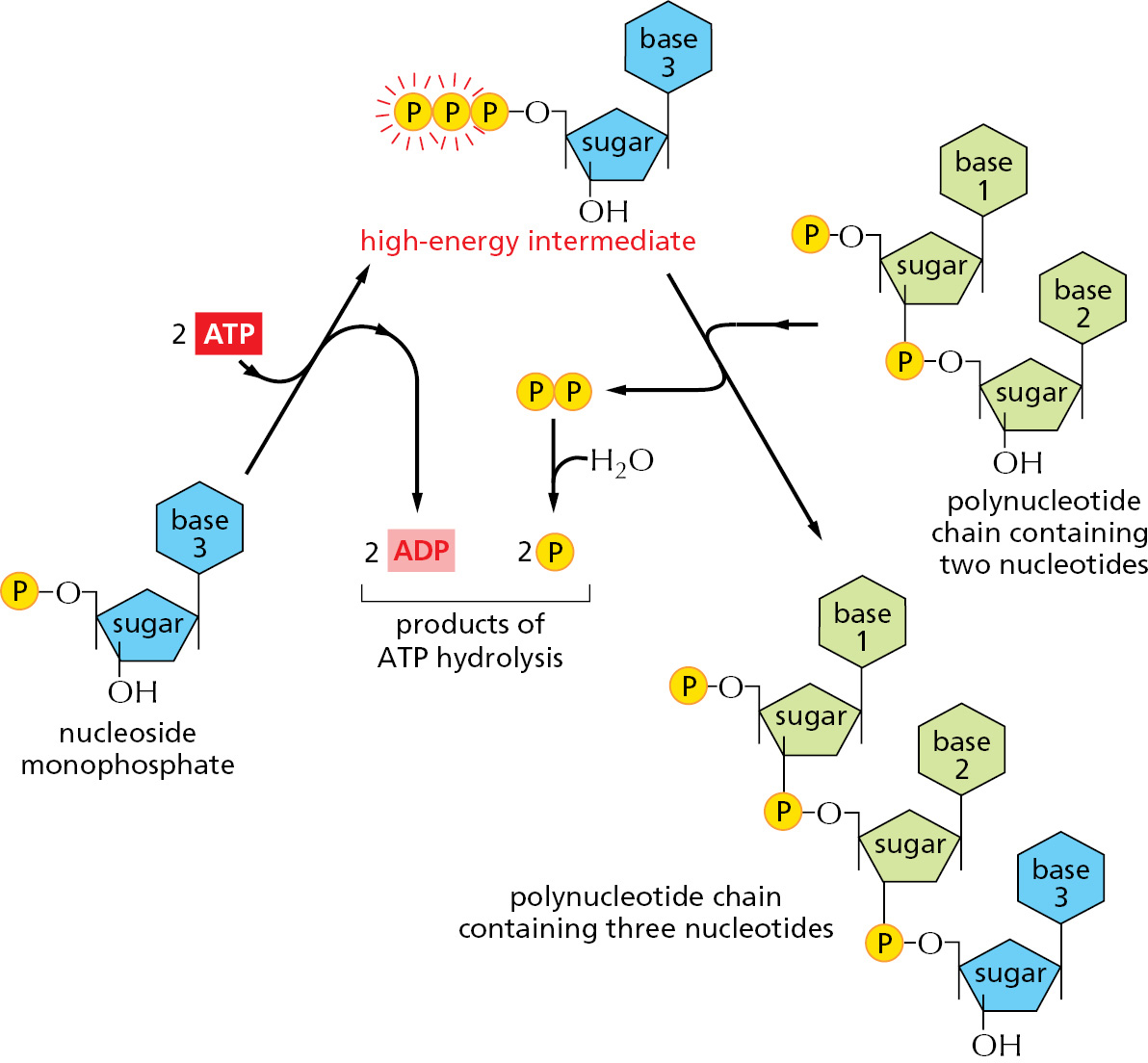
Note that the repetitive condensation reactions that produce macromolecules can be oriented in one of two ways, which differ in the position of the high-energy bond that drives polymerization. In so-called polymer-end activation, the reactive bond required for the condensation reaction is carried on the end of the growing polymer, and it must therefore be regenerated each time that a monomer is added. In this case, each monomer brings with it the reactive bond that will be used in adding the next monomer in the series. In direct-monomer activation, the reactive bond carried by each monomer is instead used immediately for its own addition (Figure 2–44).
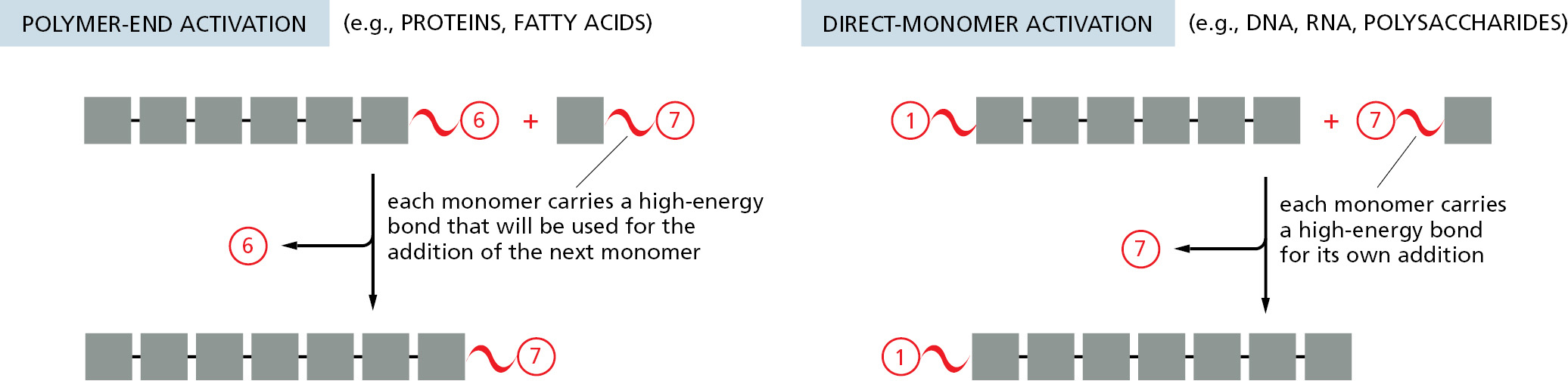
We shall see in later chapters that both of these types of polymerization are used. The synthesis of DNA, RNA, and some simple polysaccharides occurs by direct-monomer activation, for example, whereas the synthesis of proteins occurs by a polymer-end activation process.
Summary
Living cells need to create and maintain order within themselves to survive and grow. This is thermodynamically possible only because of a continual input of energy, part of which must be released from the cells to their environment as heat that disorders the surroundings. The only chemical reactions possible are those that increase the total amount of disorder in the universe. The free-energy change for a reaction, ΔG, measures this disorder, and it must be less than zero for a reaction to proceed spontaneously. This ΔG depends both on the intrinsic properties of the reacting molecules and their concentrations, and it can be calculated from these concentrations if either the equilibrium constant (K) for the reaction or its standard free-energy change, ΔG°, is known.
The energy needed for life comes ultimately from the electromagnetic radiation of the Sun, which drives the formation of organic molecules in photosynthetic organisms such as green plants. Animals obtain their energy by eating organic molecules and oxidizing them in a series of enzyme-catalyzed reactions that are coupled to the formation of ATP—a common currency of energy in all cells.
To make possible the continual generation of order in cells, energetically favorable reactions, such as the hydrolysis of ATP, are coupled to energetically unfavorable reactions. In the biosynthesis of macromolecules, ATP is used to form reactive phosphorylated intermediates. Because the energetically unfavorable reaction of biosynthesis now becomes energetically favorable, ATP hydrolysis is said to drive the reaction. Polymeric molecules such as proteins, nucleic acids, and polysaccharides are assembled from small activated precursor molecules by repetitive condensation reactions that are driven in this way. Other reactive molecules, called either activated carriers or coenzymes, transfer other chemical groups in the course of biosynthesis: NADPH transfers hydrogen as a proton plus two electrons (a hydride ion), for example, whereas acetyl CoA transfers an acetyl group.
Glossary
- enzyme
- Protein that catalyzes a specific chemical reaction.
- metabolism
- The sum total of the chemical processes that take place in living cells. All of catabolism plus anabolism.
- entropy
- (S) Thermodynamic quantity that measures the degree of disorder or randomness in a system; the higher the entropy, the greater the disorder.
- aerobic respiration
- Process by which a cell obtains energy from sugars or other organic molecules by allowing their carbon and hydrogen atoms to combine with the oxygen in air to produce CO2 and H2O, respectively.
- oxidation
- (verb oxidize) Loss of electrons from an atom, as occurs during the addition of oxygen to a molecule or when a hydrogen is removed. Opposite of reduction.
- reduction
- (verb reduce) Addition of electrons to an atom, as occurs during the addition of hydrogen to a biological molecule or the removal of oxygen from it. Opposite of oxidation.
- activation energy
- The extra energy that must be acquired by atoms or molecules in addition to their ground-state energy in order to reach the transition state required for them to undergo a particular chemical reaction.
- substrate
- Molecule on which an enzyme acts.
- catalyst
- Substance that can lower the activation energy of a reaction (thus increasing its rate), without itself being consumed by the reaction.
- diffusion
- The net drift of molecules through space due to random thermal movements.
- free energy
- (G) (Gibbs free energy) The energy that can be extracted from a system to drive reactions. Takes into account changes in both energy and entropy.
- free-energy change (∆G)
- Change in the free energy during a reaction: the free energy of the product molecules minus the free energy of the starting molecules. A large negative value of ΔG indicates that the reaction has a strong tendency to occur.
- free-energy change (∆G)
- Change in the free energy during a reaction: the free energy of the product molecules minus the free energy of the starting molecules. A large negative value of ΔG indicates that the reaction has a strong tendency to occur.
- equilibrium
- State in a chemical reaction where there is no net change in free energy to drive the reaction in either direction. The ratio of product to substrate reaches a constant value at chemical equilibrium.
- equilibrium constant
- (K) The ratio of forward and reverse rate constants for a reaction. Equal to the association or affinity constant (.a) for a simple binding reaction (A + B → AB). See also affinity constant, association constant, dissociation constant.
- ATP
- (adenosine 5’-triphosphate) Nucleoside triphosphate composed of adenine, ribose, and three phosphate groups. The principal carrier of chemical energy in cells. The terminal phosphate groups are highly reactive in the sense that their hydrolysis, or transfer to another molecule, takes place with the release of a large amount of free energy.
- ADP
- (adenosine 5’-diphosphate) Nucleotide derivative (a nucleoside diphosphate) produced by hydrolysis of the terminal phosphate of ATP. Regenerates ATP when phosphorylated by an energy-generating process such as oxidative phosphorylation.
- NAD+/NADH (nicotinamide adenine dinucleotide/reduced nicotinamide adenine dinucleotide)
- Electron carrier system that participates in oxidation–reduction reactions, such as the oxidation of food molecules. NAD+ accepts the equivalent of a hydride ion (H–, a proton plus two electrons) to become the activated carrier NADH. The NADH formed donates its high-energy electrons to the ATP-generating process of oxidative phosphorylation.
- NADP+/NADPH (nicotinamide adenine dinucleotide phosphate/reduced nicotinamide adenine dinucleotide phosphate)
- Electron carrier system closely related to NAD+/NADH, but used almost exclusively in reductive biosynthetic, rather than catabolic, pathways.
- NADH
- (nicotinamide adenine dinucleotide/reduced nicotinamide adenine dinucleotide) Electron carrier system that participates in oxidation–reduction reactions, such as the oxidation of food molecules. NAD+ accepts the equivalent of a hydride ion (H–, a proton plus two electrons) to become the activated carrier NADH. The NADH formed donates its high-energy electrons to the ATP-generating process of oxidative phosphorylation.
- NADPH
- (nicotinamide adenine dinucleotide phosphate/reduced nicotinamide adenine dinucleotide phosphate) Electron carrier system closely related to NAD+/NADH, but used almost exclusively in reductive biosynthetic, rather than catabolic, pathways.
- acetyl CoA
- Small water-soluble activated carrier molecule. Consists of an acetyl group linked to coenzyme A (CoA) by an easily hydrolyzable, energy-rich thioester bond.
- FAD/FADH2
- (flavin adenine dinucleotide/reduced flavin adenine dinucleotide) Electron carrier pair that functions in the citric acid cycle and fatty acid oxidation. One molecule of FAD gains two electrons plus two protons in becoming the activated carrier FADH2.
- activated carrier
- Small diffusible molecule that stores easily exchangeable energy in the form of one or more energy-rich covalent bonds. Examples are ATP, acetyl CoA, FADH2, NADH, and NADPH.
- coupled reaction
- Linked pair of chemical reactions in which the free energy released by one reaction serves to drive the other.
- standard free-energy change ΔG°
- The change in free energy under a standard condition, defined as that where the concentrations of all the reactants are set to the same fixed value of 1 mole/liter.