SPECIAL TOPICA Primer on Game Theory
Game theory is a tool for analyzing strategic interactions. Over the last 50 years, it has been developed and applied broadly in nearly all the social sciences, as well as in biology and other physical sciences—and it is even making inroads in the humanities. Among its earliest and most useful applications was international politics. We provide here a brief overview of game theory to introduce strategic thinking and illustrate concepts discussed in the text.
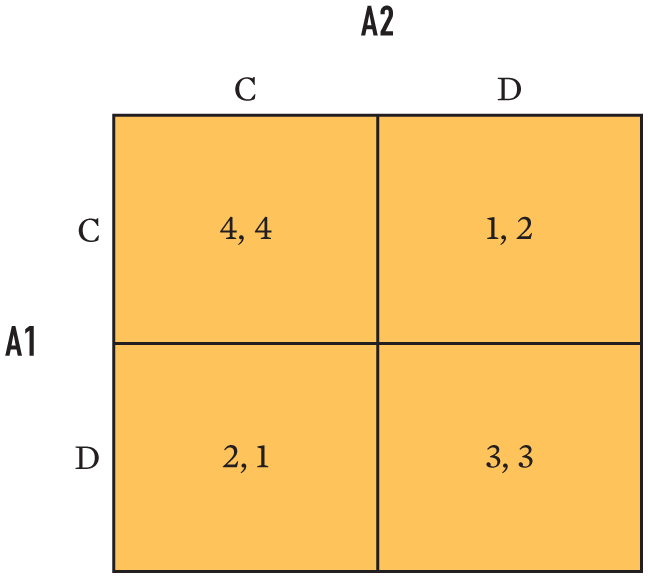
Imagine two actors, Actor 1 (A1) and Actor 2 (A2), with only two choices, which we call cooperation (C) and defection (D). Since each actor has two choices, there are four possible outcomes to this “game”: both might cooperate (CC), both might defect (DD), A1 might cooperate while A2 defects (CD), and A1 might defect while A2 cooperates (DC). The mapping of choices into outcomes is best depicted using a 2 × 2 matrix, as shown in Figure A.1.a As defined in the chapter text, the actors’ interests determine how they rank the four possible outcomes from best (4) to worst (1), with higher “payoffs” representing more preferred outcomes. A1’s payoffs are given first in each cell; A2’s are given second.
Both actors choose simultaneously without knowledge of the other’s choices but with knowledge of their own preferences and those of the other actor.b The outcome we observe is a function of the interaction—that is, the choices of both actors. Each actor can choose only C or D, but their payoffs differ across the four possible outcomes. Suppose A1 chooses C and ranks CC (mutual cooperation) over CD. In choosing C, A1 only partially controls which outcome arises; A1’s actual payoff depends crucially on whether A2 chooses C (creating CC) or D (creating CD). This scenario highlights a key point: that strategic interaction depends on the choices of all relevant actors, and a strategic interaction framework is thus most useful in explaining situations in which outcomes are contingent on the choices of all parties.
In such a setting, purposive actors—that is, actors who seek their highest expected payoff—choose strategies, or plans of action, that are a best response to the anticipated actions of the other. Sometimes it makes sense for an actor to make the same choice (C or D) regardless of what the opponent does; in these cases, the actor is said to have a dominant strategy. In other cases, each player’s best choice depends on what the opponent does. For example, a player’s best response might be to cooperate when the other side cooperates and defect when the other side defects.
Since each actor is trying to play its best response, and since each expects the other to play its own best response, the outcome of the game is determined by the combination of the two actors’ strategies, each of which is perceived to be a best response to the other. An outcome that arises from each side choosing best-response strategies is called an equilibrium. An equilibrium outcome is stable because the actors have no incentive to alter their choices; since, in equilibrium, both are playing their best responses, by definition they cannot do better by changing their choices. In the game illustrations that follow, the equilibrium (or equilibria, when there is more than one) is denoted by an asterisk (*) in the appropriate cell.
The Prisoner’s Dilemma
As described in the text (pp. 59–60), the Prisoner’s Dilemma is a commonly cited game in international relations because it captures problems of collaboration, such as arms races and the provision of public goods. Reread the full text on pp. 59–60, and keep in mind that each prisoner can either cooperate with his accomplice and refuse to provide evidence to the district attorney or defect on his accomplice by ratting him out. Therefore, four different outcomes are possible for each player, ranked as follows:
- Best outcome (ranked 4): The prisoner defects while his partner cooperates (DC), meaning that he is freed immediately, while his partner is jailed for 10 years.
- Second-best outcome (3): The prisoner and his partner both cooperate (CC), and therefore each spends only 1 year in prison.
- Third-best outcome (2): The prisoner and his partner both defect (DD), and each is imprisoned for 5 years.
- Worst outcome (1): The prisoner cooperates while his partner defects (CD), meaning that he goes to prison for 10 years while his partner goes free.
In short, each prisoner has identical interests and ranks the four possible outcomes as DC > CC > DD > CD (the “greater than” symbol should be read in each case as meaning that the first outcome is “preferred over” the second), as depicted in Figure A.2.
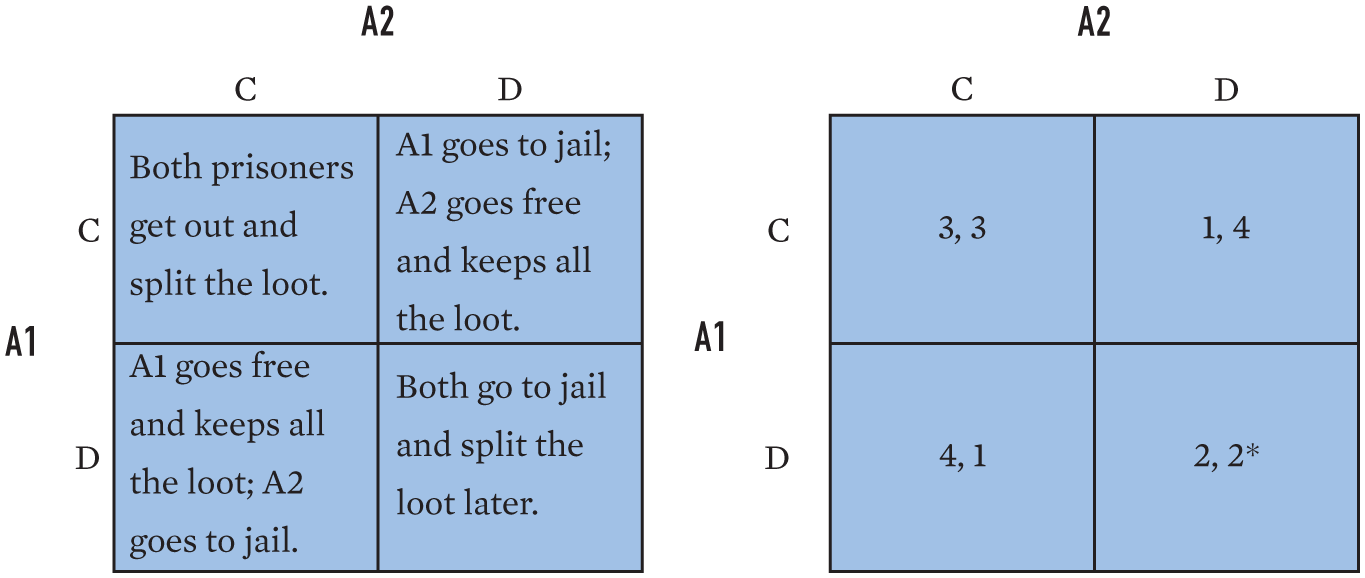
What each prisoner should do is unclear at this point, but here is where the techniques of game theory help. As close examination of the matrix reveals, each criminal’s dominant strategy is to defect, regardless of his partner’s actions. If his partner cooperates (that is, stays quiet), he is better off defecting (that is, talking to the district attorney) (DC > CC). If his partner defects, he is also better off defecting (DD > CD). The equilibrium that results from each prisoner playing his best response is DD, or mutual defection. The paradox, or dilemma, arises because both criminals would in fact be better off if they remained silent and got released relatively quickly than if they both provided evidence and went to jail (CC > DD). But despite knowing this, each still has incentives to defect in order to get off easy (DC) or at least safeguard against his partner’s defection (DD). The only actor who wins in this contrived situation is the district attorney, who sends both criminals to jail.
Although it is a considerable simplification, many analysts have used the Prisoner’s Dilemma to capture the essential strategic dilemma at the core of the collective action problem. Each individual prefers free riding while others contribute to the public good of, say, national defense, (DC) over contributing if everyone else does and receiving the good (CC), over not contributing if no one else does (DD), and finally over contributing if no one else contributes (CD). As with the prisoners, each individual has a dominant strategy of not contributing (that is, defecting); thus, the public good of national defense is not provided voluntarily. The dilemma is solved only by the imposition of taxes by an authoritative state.
Chicken
The game of Chicken represents a second strategic dilemma. The animating story here is the game played by teenagers in the 1950s (and perhaps today by teenagers not yet familiar with game theory!). Two drivers speed down the middle of the road toward one another. The first to turn aside, the “chicken,” earns the derision of his or her peers. The other driver wins. If both swerve simultaneously, neither is humiliated. If neither turns aside, both risk death in a serious wreck. If turning aside is understood as cooperation and continuing down the middle of the road as defection, the actors’ interests are DC > CC > CD > DD, as shown in Figure A.3 (note that this is the same order of preferences as in the Prisoner’s Dilemma, except for the reversal of the last two outcomes).
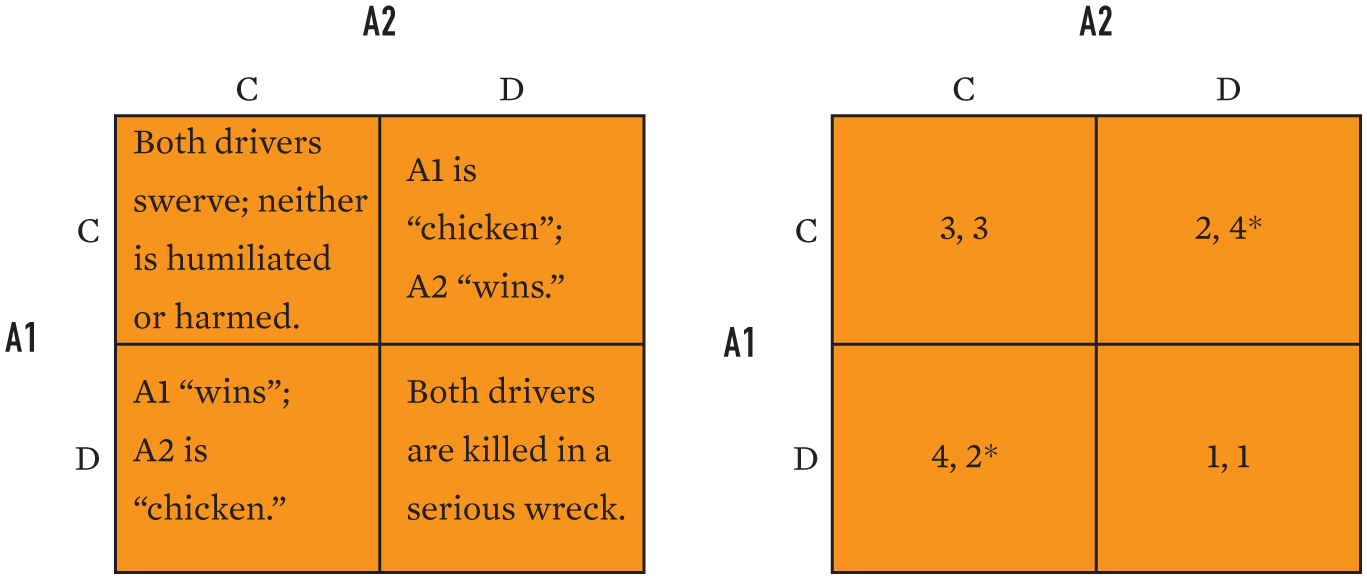
Lacking a dominant strategy, the key to one’s strategy in Chicken is to do the opposite of what you think the other driver is likely to do. If you think your opponent will stand tough (D), you should turn aside (C). If you think your opponent will turn aside (C), you should stand tough (D). Two equilibria exist (DC and CD). The winner is the driver who by bluster, swagger, or past reputation convinces the other that she is more willing to risk a crash.
Chicken is often taken as a metaphor for coercive bargaining (see p. 67 in the text). Nuclear crises are usually thought of as Chicken games. Both sides want to avoid nuclear disaster (DD), but each has incentives to stand tough and get the other to back down (DC). The state willing to take the greatest risk of nuclear war is therefore likely to force the other to capitulate. The danger, of course, is that if both sides are willing to run high risks of nuclear war to win, small mistakes in judgment or calculation can have horrific consequences.
The Stag Hunt
A final game, which is often taken as a metaphor for problems of coordination in international relations (see p. 59 in the chapter text), is the Stag Hunt. This is one of a larger class of what are known as assurance games.c The motivating parable was told by political philosopher Jean-Jacques Rousseau. Only by working together can two hunters kill a stag and feed their families well. One must flush the deer from the forest, and the other must be ready to fire his arrow as the animal emerges. In the midst of the hunt, a lone rabbit wanders by. Each hunter now faces a decision: he could capture the rabbit alone, but to do so he must abandon the stag, ensuring that it will get away.
A rabbit is good sustenance but not as fine as the hunter’s expected share of the stag. In this game, both hunters are best off cooperating (CC) and sharing the stag. The next-best outcome is to get a rabbit while the other tries for the stag (DC); however, if both go for the rabbit (DD), they then split the rabbit. The worst outcome for each hunter is to spend time and energy hunting the stag while the other hunts the rabbit (CD), leaving him and his family with nothing. Thus, each hunter’s interests create the ranking CC > DC > DD > CD, as depicted in Figure A.4.
Despite the clear superiority of mutual cooperation, a coordination dilemma arises. If each hunter expects that the other will cooperate and help bring down the stag, each is best off cooperating in the hunt. But if each expects that the other will be tempted to defect and grab the rabbit, thereby letting the stag get away, he will also defect and try to grab the rabbit. Lacking a dominant strategy, each can do no better than what he expects the other to do—creating two equilibria (CC and DD).

The Stag Hunt captures situations in which the primary barrier to cooperation is not an individual incentive to defect but a lack of trust. If we define trust in this context as an expectation that the partner will cooperate, then trust leads to mutual cooperation while a lack of trust leads to mutual defection. (By contrast, in the Prisoner’s Dilemma it never makes sense to trust an accomplice, and if one accomplice expects the other accomplice to cooperate, the best response is to defect.) Imagine, for example, two states have placed their military forces at their border in order to defend against a possible attack from the other side. Since having troops close to the border creates a risk of an accident, the states could cooperate by withdrawing their forces some distance from the border. If neither state wants to attack, then reducing the risk of accident through mutual withdrawals (CC) is better than leaving forces at the border, even unilaterally (DC). But neither state wants to be the only one to withdraw (CD < DD). In this scenario, each state will withdraw if it trusts that the other will withdraw, and each will keep its forces in place if it does not trust that the other will withdraw.
As this brief survey suggests, game theory helps clarify the core dilemmas in certain types of strategic situations. Many games are far more complex than the examples described here, with more possible actions than “cooperate” or “defect,” information asymmetries, random chance, and many more devices to capture elements of real-world strategic situations. The games presented here are more like metaphors than accurate representations of actual situations in international relations. But they illustrate how thinking systematically about strategic interaction helps us understand why actors cannot always get what they want—and, in fact, often get rather disappointing outcomes, even though all actors might prefer other results. In both the Prisoner’s Dilemma and the Stag Hunt, for instance, all actors prefer CC over DD, and this mutual preference is known in advance. Nonetheless, in the Prisoner’s Dilemma mutual defection is the equilibrium result, and in the Stag Hunt it is one of two expected outcomes. In all three games, outcomes are the result of the choices not of one actor, but of all.
Endnotes
- The same games can be represented in extensive form as a “game tree.” Both are common in the larger literature. Return to reference a
- In some of the games discussed here, the outcome does not depend on the assumption that the actors move simultaneously. Return to reference b
-
Another common assurance game captures situations in which two actors want to coordinate on the same action, but they have different preferences. For example, two friends want to spend the evening together, but one wants to attend a sporting event and the other a movie. The worst outcome for each is to spend the evening alone. Interested readers should model this game and describe its dynamics in terms similar to those for the Stag Hunt and the other games in this appendix.Return to reference c