1.7 Bond Strength
In Figure 1.42, the energy of the electrons in the two atomic orbitals is greater than their energy in the bonding molecular orbital ΦB. As noted earlier, lower energy means greater stability, but just how much energy is the stabilization apparent in Figure 1.42 worth? The difference between the energies of the two electrons in ΦB and the energies of the two separate electrons in atomic 1s orbitals is 104 kcal/mol (435 kJ/mol). This amount of energy is very large, and consequently the H2 molecule is held together (bound) by a substantial amount of energy. This same amount of energy is released into the environment if H2 molecules are formed from separated hydrogen atoms. It would require the application of exactly this amount of energy to generate two hydrogen atoms from a molecule of H2. The 104 kcal/mol represents the stabilization of two electrons in ΦB (Fig. 1.44).
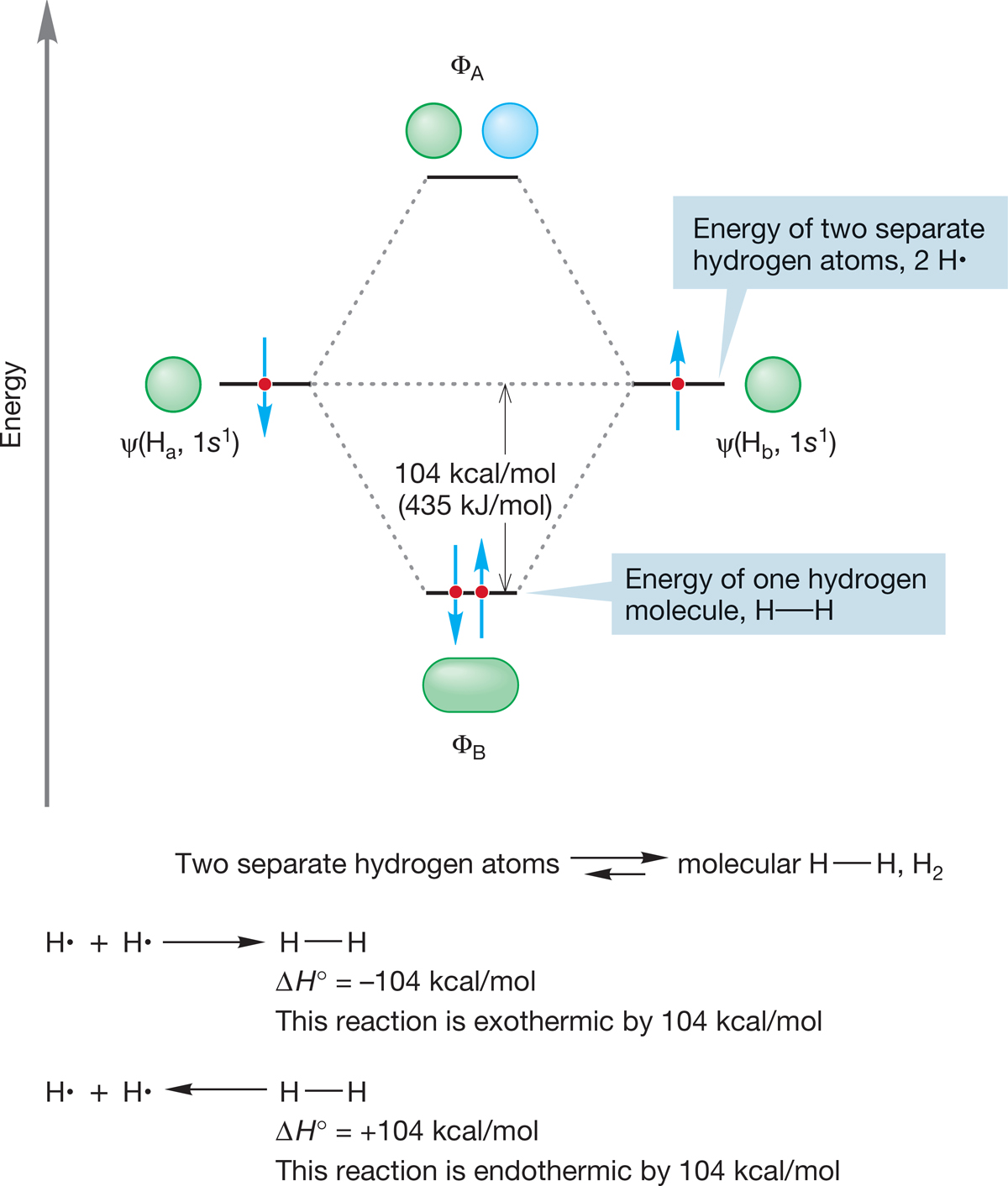
FIGURE 1.44 Molecular hydrogen (H2) is more stable than two isolated hydrogen atoms by 104 kcal/mol.
Actually, if we could measure it, the temperature would rise ever so slightly as two hydrogen atoms combined to make a hydrogen molecule because 104 kcal/mol would be released as heat energy into the vessel. The environment in the vessel would warm up as the process proceeded. A reaction that liberates heat, one where the products are more stable than the starting materials, is called an exothermic reaction. The opposite situation, in which the products are less stable than the starting materials, requires the application of heat and is called an endothermic reaction.
The enthalpy change (ΔH°) of any chemical reaction is estimated as the difference between the total bond energy of the products and the total bond energy of the reactants. The value of ΔH° for a reaction between hydrogen atoms to give H2 is −104 kcal/mol (−435 kJ/mol).
CONVENTION ALERT
Exothermic versus Endothermic Reactions
The sometimes troublesome sign convention shows ΔH° for an exothermic reaction as a negative quantity. For an endothermic reaction, ΔH° is positive. For example,
If A + B→C ΔH° = −x kcal/mol, then the reaction is exothermic
If A + B→C ΔH° = +x kcal/mol, then the reaction is endothermic
In Figure 1.44,
H· + H· → H―H ΔH° = −104 kcal/mol, an exothermic reaction
From this we can also know that the reverse reaction
H—H → H· + H· ΔH° = +104 kcal/mol, is an endothermic reaction
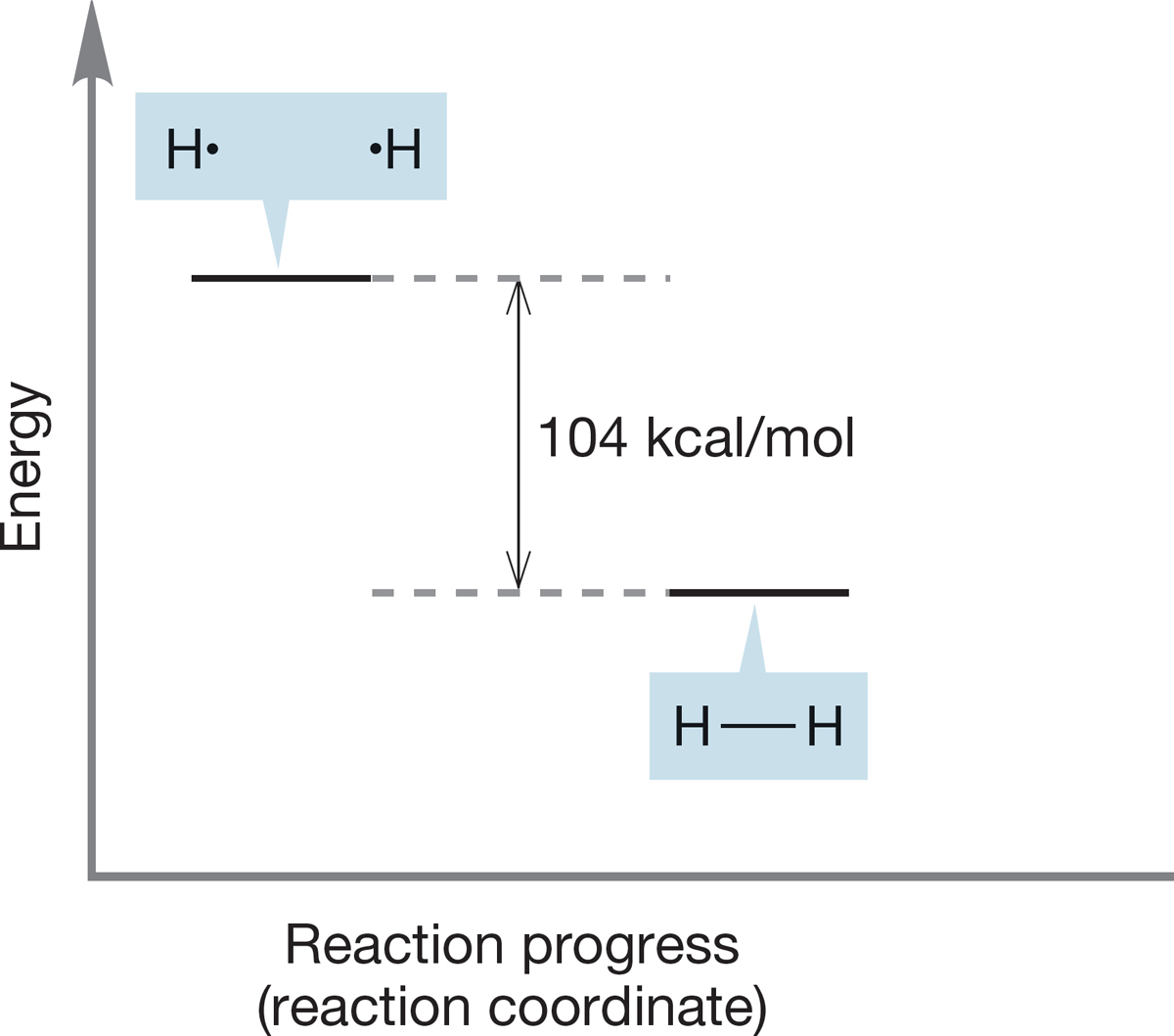
FIGURE 1.45 Another schematic picture of the formation of molecular hydrogen from two hydrogen atoms.
Figure 1.45 plots the energy of reactants and products in a chemical reaction against a variable known either as the reaction progress or the reaction coordinate. A reaction coordinate monitors a change or changes taking place as the reaction proceeds. These changes may be distance between atoms, angles between bonds, or a combination of relationships that result from the movement of atoms. For example, in the reaction H· + H· → H2, a suitable reaction coordinate might be the distance between the two hydrogen atoms. It is a fair approximation at this point to take this “reaction coordinate” as indicative of the progress of the overall reaction, and for that reason we will use the term reaction progress from now on.
A reaction progress graph can be read either left to right or right to left. Reading Figure 1.45 left to right tells us that the energy of the product is lower than the energy of the reactants, so the graph shows the release of energy, in this case, 104 kcal/mol, as H2 is formed in an exothermic reaction. If we read the graph from right to left, we see the endothermic formation of two hydrogen atoms from the H2 molecule.
This amount of energy that must be added to break the H2 bond and produce two hydrogen atoms, 104 kcal/mol, is called the bond dissociation energy (BDE). It is the amount of energy that must be applied for homolytic bond cleavage. The higher the BDE, the more difficult it is to break the bond. A bond can break in either of two ways (Fig. 1.46). In homolytic cleavage, one electron from the bond goes with one atom and the other electron of the bond goes with the other atom. This kind of bond cleavage gives neutral species. The other option for bond breaking has both electrons from the bond go to the same atom, creating an anion–cation pair. This process is called heterolytic bond cleavage. Normally, heterolytic cleavage of nonpolar bonds is not the path followed because it usually costs more energy to develop separated charges than to make neutral species.

FIGURE 1.46 In one kind of bond cleavage, the pair of binding electrons is split evenly between the atoms, giving a pair of neutral species. This lower-energy process is called homolytic cleavage. Heterolytic cleavage produces a pair of ions.
CONVENTION ALERT
Single-Barbed versus Double-Barbed Curved Arrows
Notice the difference in the red curved arrows in the two parts of Figure 1.46. The curved arrow showing electron movement in the heterolytic cleavage is the standard double-barbed arrow, which represents the movement of two electrons to the same atom. The homolytic cleavage pathway uses the single-barbed, or “fishhook,” arrow, which represents the movement of one electron to an atom.
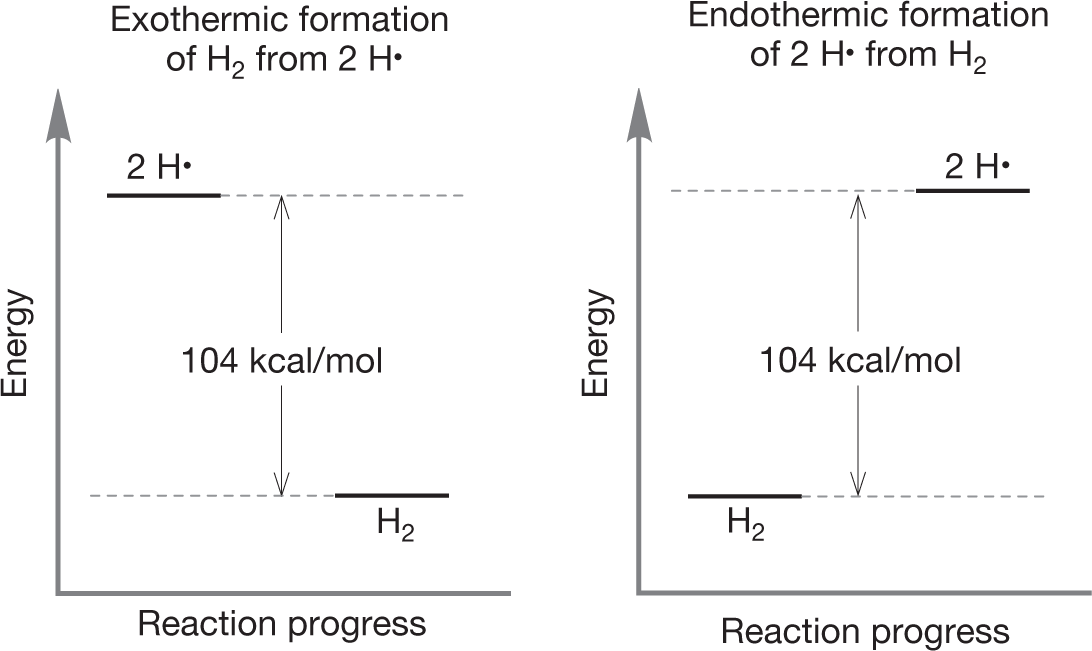
WORKED PROBLEM 1.27 Sketch the profile of an endothermic reaction. See Figure 1.45 for the sketch of an exothermic reaction.
ANSWER Aha! A trick question. If you have written an exothermic reaction, you have already written an endothermic reaction as well. You need only read your answer backward. We are psychological prisoners of our tendency to read from left to right. Nature has no such hangups! The formation of molecular hydrogen from two hydrogen atoms (Fig. 1.45, left to right) is exothermic (104 kcal/mol of energy is given off as heat), and the formation of two hydrogen atoms from a single hydrogen molecule is endothermic by the same amount (104 kcal/mol of heat energy must be applied).
In practice, a reaction that requires about 15–20 kcal/mol (63–84 kJ/mol) of thermal energy proceeds quite reasonably at room temperature, about 25°C. It is important to begin to develop a feeling for which bonds are strong and which are weak to start to build up a knowledge of approximate bond strengths.9 The bond in the hydrogen molecule is a strong one. As we continue our discussion of structure, we’ll make a point of noting bond energies as we go along. Table 1.10 gives a few important bond dissociation energies. Some instructors might expect you to remember some of the bond energies. It is more likely that you will be expected to remember and understand the reason for the trends. Notice the following: (1) the bond strength decreases in the order C―F > C―Cl > C―Br > C―I (this order is because of poor overlap between orbitals with different principal quantum numbers). For the same reason, H―F > H―Cl > H―Br > H―I is the order of bond strength for the halogen acids. (2) The order of bond strength for carbon–carbon bonds is C―C < C C < C
C < C C, and the same trend exists for the carbon–nitrogen bonds C―N < C
C, and the same trend exists for the carbon–nitrogen bonds C―N < C N < C
N < C N. More bonds need to be broken to separate the atoms in going from a single bond to a double bond and then to the triple bond.
N. More bonds need to be broken to separate the atoms in going from a single bond to a double bond and then to the triple bond.
TABLE 1.10 Some Average Bond Dissociation Energies
BDE |
BDE | ||||
Bond |
kcal/mol |
kJ/mol |
Bond |
kcal/mol |
kJ/mol |
C―H |
96–105 |
402–440 |
C |
~175 |
~733 |
N―H |
93–107 |
389–448 |
C |
~143 |
~599 |
O―H |
110–119 |
461–498 |
C |
~177 |
~741 |
S―H |
82–87 |
343–364 |
C |
~230 |
~963 |
C―C |
83–90 |
348–377 |
C |
~204 |
~854 |
C―N |
69–75 |
289–314 | |||
C―O |
85–96 |
356–402 | |||
C―F |
105–115 |
440–481 |
H―F |
136 |
569 |
C―Cl |
83–85 |
348–356 |
H―Cl |
103 |
431 |
C―Br |
72–74 |
301–310 |
H―Br |
88 |
368 |
C―I |
55–57 |
230–239 |
H―I |
71 |
297 |
BDE, bond dissociation energy.
PROBLEM 1.28 Notice in Table 1.10 that the C―H bond is about the same strength as the C―F bond. Organic chemists use this fact in design of pharmaceutical drugs, many of which have C―F groups. The fluorine has about the same size and has a similar bond strength to carbon as does an H. What other attributes might an F bring to a drug?
Table 1.10 gives averages over a range of compounds. A few compounds may lie outside these values. In later chapters, more precise values of specific bonds will appear.
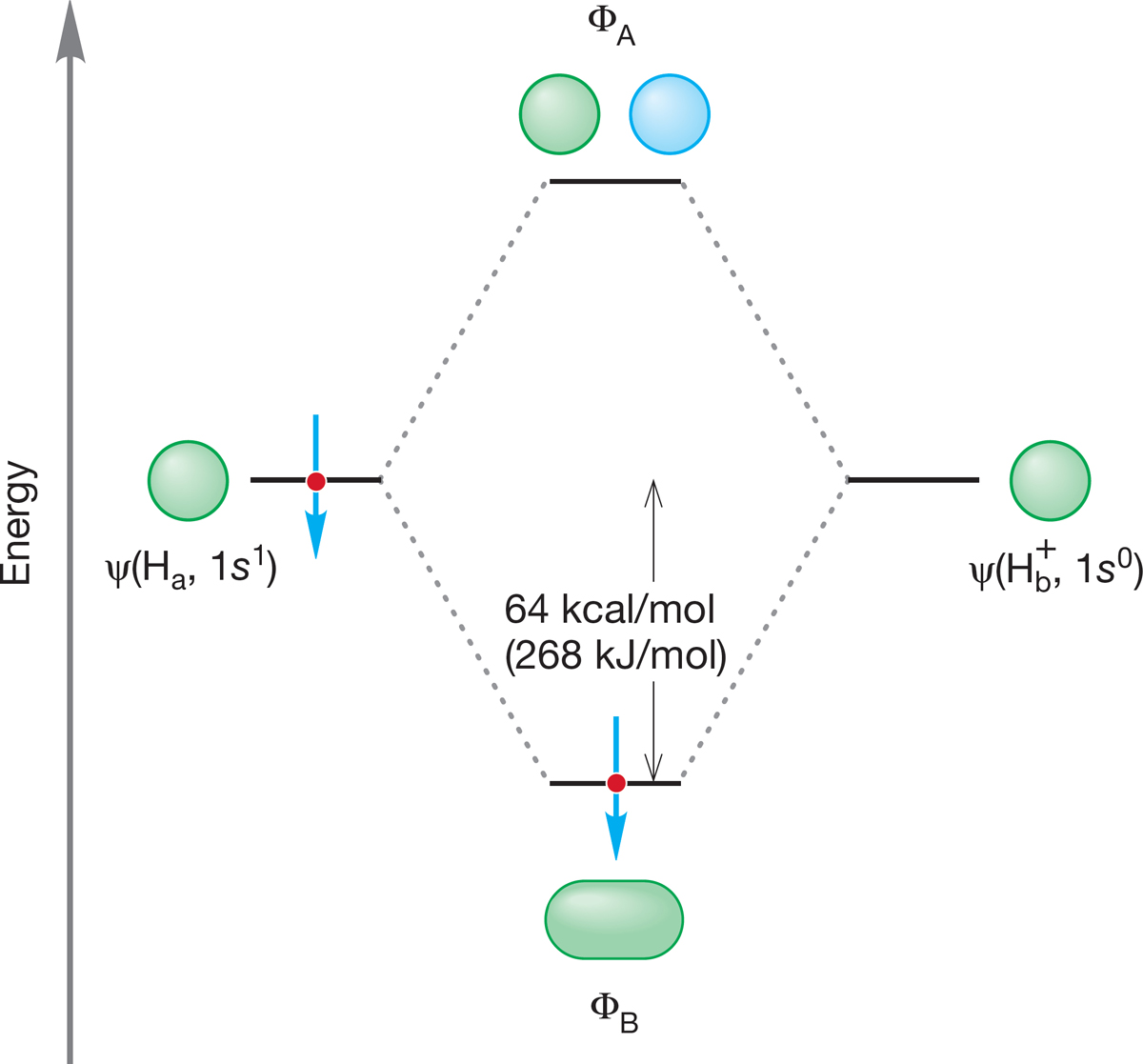
FIGURE 1.47 An orbital interaction diagram for H2+.
Let’s consider the simplest molecule, H2+, which is H2 with only one electron and a positive charge. Even this molecule is bound quite strongly.10 The small amount of information already in hand—a molecular orbital picture of H2 and the bond strength of the H―H bond (104 kcal/mol)—enables us to construct a picture of this exotic molecule and to estimate its bond strength. We can imagine making H2+ by allowing a hydrogen atom, H·, to combine with H+, a bare proton. All the work necessary to create an orbital interaction diagram for this reaction was done in the construction of Figure 1.41. We are still looking at the combination of a pair of hydrogen 1s atomic orbitals, so the building of a diagram for H2+ produces precisely the same orbital diagram, reproduced in Figure 1.47. The only difference comes when we put in the electrons. Instead of having two electrons, as does H2, with one coming from each hydrogen atom, H2+ has only one electron. Naturally, it goes into the lower-energy, bonding molecular orbital, ΦB. The electron spin is shown down, but it could equally well be shown up. There is no difference in energy between the two spins, and we have no way of knowing which way a single spin is oriented.
What might we guess about the bond energy of this molecule H2+? If two electrons in ΦB result in a bond energy of 104 kcal/mol, it seems reasonable to guess first that stabilization of a single electron would be worth half the amount, or about 52 kcal/mol (218 kJ/mol). That is, when an H· atom and an H+ ion combine to form the species H2+, we are estimating that 52 kcal/mol of heat is given off. And we are amazingly close to being correct! It has been experimentally determined that the H2+ molecule is bound by 64 kcal/mol (Fig. 1.47), which means that the system H2+ is 64 kcal/mol (268 kJ/mol) more stable than the system of a separated H· and H+.
PROBLEM 1.29 Although our guess of 52 kcal/mol is quite close to the actual value, it is a bit low. In other words, the H2+ molecule is more stable (lower in energy) than we thought. Why is our estimate of bond strength a little low? To ask the same question another way, why might the stabilization of two electrons in an orbital be less than twice the stabilization of one electron in the orbital? Hint: Consider electron–electron repulsion.
It may seem somewhat counterintuitive that a low-energy (strong) bond is associated with a large number for the BDE. The lower the energy of a bond, the higher the number representing bond strength! The low-energy, strong bond in H2 has a BDE of 104 kcal/mol, for example, whereas the higher-energy, weaker bond in H2+ has a BDE of only 64 kcal/mol. A strong bond means a low-energy, stable species. The diagram in Figure 1.44 should help keep this point straight. A strong bond means a more stable bond and it means a lower position on an energy diagram.
Remember the sign convention: 2 H· → H―H, ΔH° = −104 kcal/mol. The minus sign tells us that this reaction is exothermic as read from left to right. An exothermic reaction will have products that are more stable than the starting materials. The products will be lower than the reactants on the energy diagram.
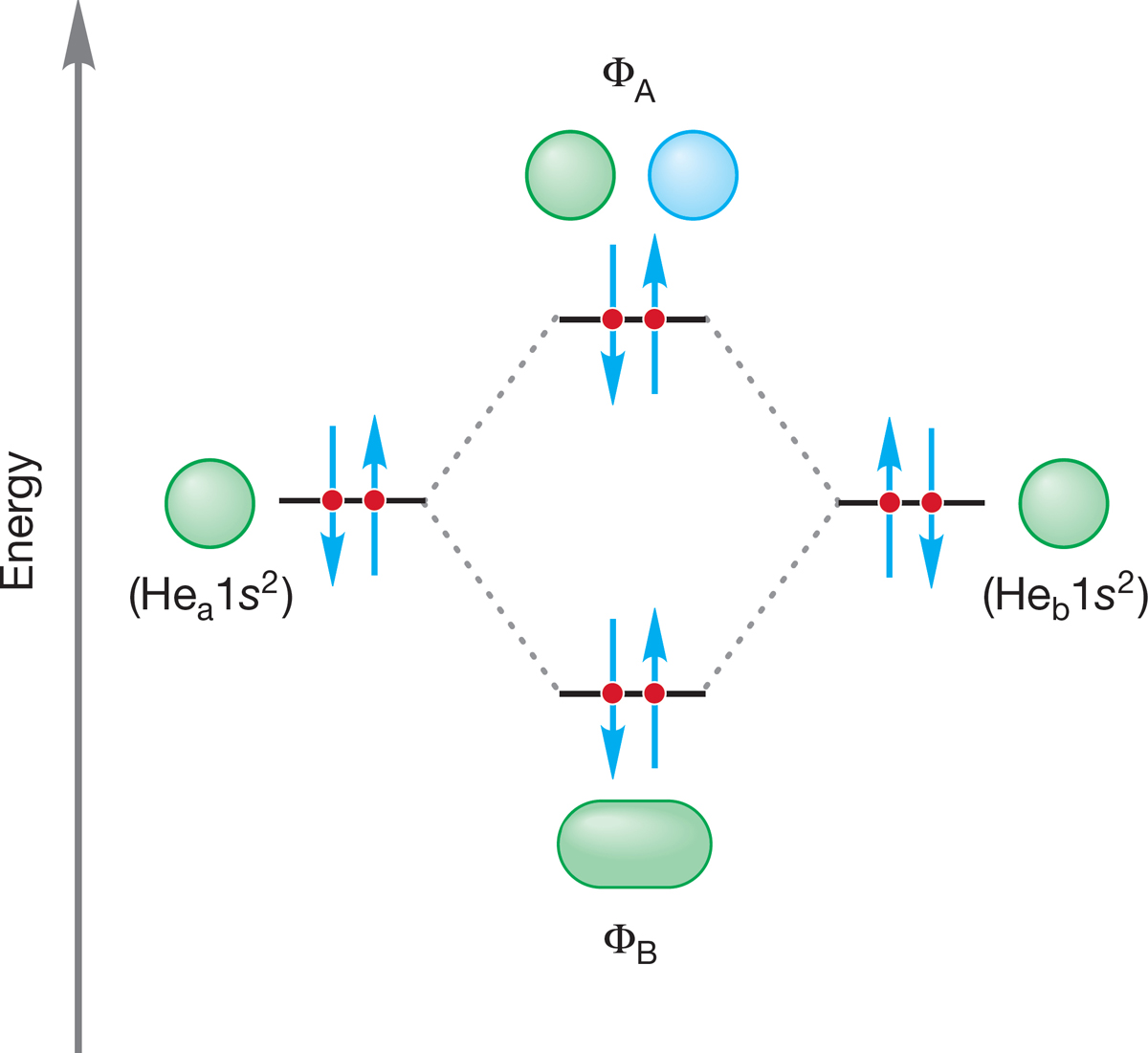
FIGURE 1.48 An orbital interaction diagram for He2. No net bonding occurs because the stabilization owing to the pair of electrons in the bonding molecular orbital is offset by the destabilization from the two electrons in the antibonding orbital.
The antibonding molecular orbital (ΦA) has been empty in all of the examples we have considered. Why the emphasis on ΦA? What is an empty orbital, anyway? The easiest, nonmathematical way to think of ΦA in H2 is as the place the next electron would go. If the bonding molecular orbital ΦB is filled, as it is in H2, for example (Fig. 1.44), another electron cannot occupy ΦB and must go instead into the antibonding orbital, ΦA. This would create H2− (H2 + e− → H2−).
Dihelium, He2, a strictly hypothetical species, is an example of a molecule in which electrons must occupy antibonding orbitals. Each He, like each H in H2, brings only a 1s orbital to the mixing. Just as in the molecules H2 and H2+, the molecular orbitals for He2 are created by the combination of two 1s atomic orbitals (Fig. 1.48). Each helium atom brings two electrons to the molecule, though, so the electronic occupancy of the orbitals is different from that for H2 or H2+. The bonding orbital (ΦB) can hold only two electrons (Pauli principle) so the next two must occupy ΦA. The two electrons in this antibonding orbital are destabilizing to the molecule, just as the two electrons in ΦB are stabilizing. As a result, no net bonding occurs in the hypothetical molecule He2. The stabilization afforded by the two electrons in the bonding molecular orbital is canceled by the destabilization resulting from the two electrons in the antibonding molecular orbital. Molecular helium He2 is, in fact, unknown.
Summary
The energy of an electron in a bonding molecular orbital generated through mixing of two orbitals depends primarily on the extent of mixing between the two orbitals that combine to produce it. Extensive interaction leads to a low-energy bonding molecular orbital (and a high-energy antibonding molecular orbital). Thus, one or two electrons in such an orbital will be well stabilized. The bond joining the two atoms is strong. Orbitals that are orthogonal do not mix. This molecular orbital (MO) treatment of bonding explains why some bonds are weak and some are strong. Rather than memorizing bond energies, we can explain “why” the energies associated with each bond are higher or lower. It’s all based on orbitals. Why is a C―F bond strong? It is because there is good overlap between the orbitals of the carbon and the fluorine. Why is the C―I bond weak? It is because the orbital overlap between the carbon and the iodine is poor. The carbon uses an orbital from the second shell and the iodine uses an orbital from the sixth shell. Understanding “why” bonds are weak or strong will help you remember, and more important, it will help you predict.
PROBLEM 1.30 Draw the orbital interaction diagram for He2+.
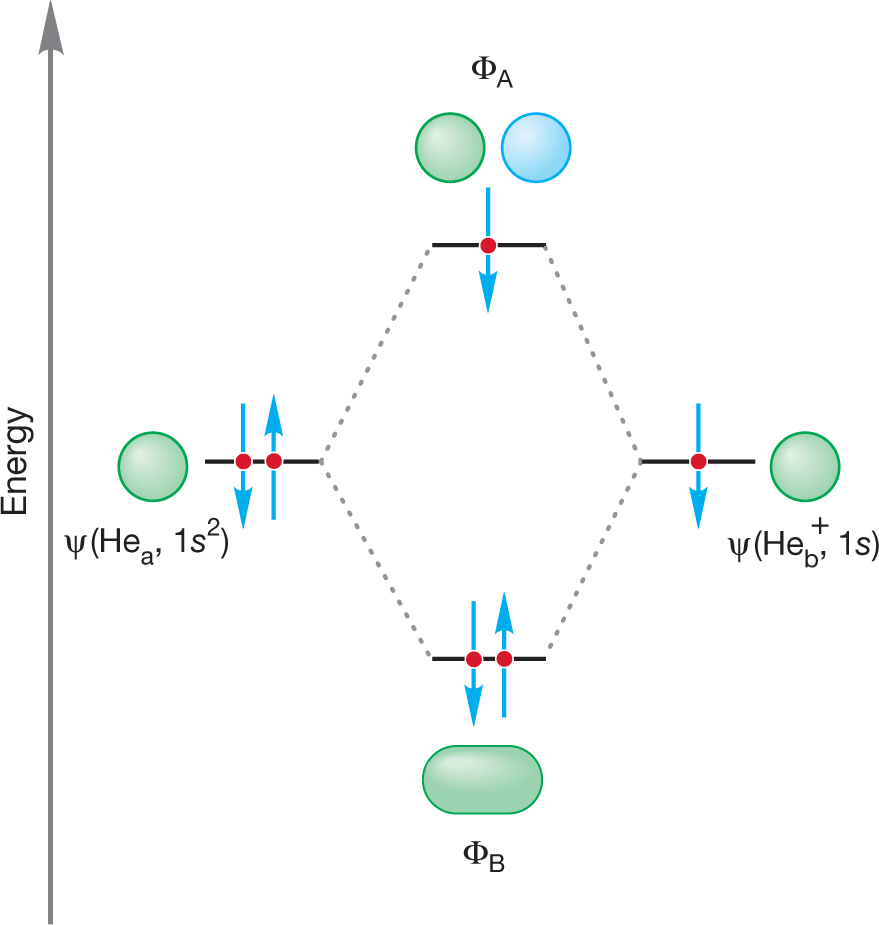
WORKED PROBLEM 1.31 Estimate the bond strength for He2+. Show how you arrived at your estimate.
ANSWER The molecular orbital diagram for this molecule can be derived from Figure 1.48 by removing one electron. The He2+ molecule can be constructed from He and He+. This molecule has only three electrons. Assuming that an electron in the antibonding orbital ΦA destabilizes the molecule about as much as an electron in the bonding orbital ΦB stabilizes the molecule, there is one net bonding electron in this molecule (2 bonding electrons − 1 antibonding electron = 1 net bonding electron). The He2+ should have a bond strength about the same as that of H2+, another molecule with a single electron in the bonding molecular orbital. This estimate turns out to be correct. The bond energy for He2+ has been experimentally measured to be about 60 kcal/mol (251 kJ/mol).
PROBLEM 1.32 Use the answer to Problem 1.29 to work out the answer to a more subtle question. In He2, both the bonding and the antibonding molecular orbitals are filled with two electrons. Consider electron–electron repulsion to explain why the stabilization of the two electrons in ΦB is less than the destabilization of the electrons in ΦA.
9To describe a bond as strong or weak is an arbitrary function of human experience. A bond that requires 100 kcal/mol (418 kJ/mol) to break is “strong” in a world where room temperature supplies much less thermal energy. It would not be strong on the sunlit side of Mercury (where it’s hot: the average temperature is about 377°C, or 710°F). Similarly, if you were a life form that evolved on Pluto (where it’s cold: the average temperature is about −220°C, or −361°F), you would regard as strong all sorts of “weak” (on Earth) interactions, and your study of chemistry would be very different indeed. One area of research in organic chemistry focuses on extremely unstable molecules held together by weak bonds. The idea is that by understanding extreme forms of weak bonding, we can learn more about the forces that hold together more conventional molecules. Chemists who work in this area deliberately devise conditions under which species that are normally most unstable can be isolated. They create very low temperature “worlds” in which other reactive (predatory) molecules are absent. In such a world, exotic species may be stable, as they are insulated from both the ravages of heat (thermodynamic stability) and the predations of other molecules (kinetic stability).
10Here is the answer to Problem 1.23. The simplest molecule is hydrogen (H2) minus one electron. Another electron cannot be removed to give something even simpler because H22+ is not a molecule―there are no electrons to bind the two nuclei.