1.6 Hydrogen (H2): Molecular Orbitals
In the first part of this chapter, we examined atomic structure and atomic orbitals, and we began a study of the collections of atoms called molecules. Now we enlarge the discussion to include molecular orbitals, the regions of space occupied by electrons in molecules. Covalent bonding between atoms involves the sharing of electrons. This sharing takes place through overlap of an atomic orbital with another atomic orbital or with a molecular orbital.
It’s a jungle out there! A century ago, when chemistry was a young science, there seemed to be little time to worry too much about the “how and why” of the science; there was too much discovering going on, too much information to be collected. Here is what Friedrich Wöhler (1800–1882), a great early unifier of organic chemistry, had to say on the subject: “Organic chemistry just now is enough to drive one mad. It gives one the impression of a primeval, tropical forest full of the most remarkable things, a monstrous and boundless thicket, with no way of escape, into which one may well dread to enter.” Nowadays, no longer is some metaphoric vast jungle being explored by brute force; chemists are now thoughtfully aiming more and more at new discoveries. The more we understand, and the better our models of nature are, the more likely it is that the current transformation from trial-and-error methods to intellectually driven efforts will be successful.
Chemistry is largely the study of the structure and reactivity of molecules. Molecular orbital calculations provide us with the most accurate prediction of structure and reactivity of a molecule. Understanding of chemistry depends on understanding how molecules react and on the application of that understanding in creative ways. The idea that both the structures of molecules and the reactions they undergo can be understood by examining the shapes and interactions of atomic and molecular orbitals has gained widespread acceptance in the chemical community, and an important branch of theoretical chemistry embraces these ideas. Although the study of molecular orbitals can be approached in a highly mathematical way, we will not follow that path. One of the great benefits of our nonmathematical approach is that it can be appreciated quite readily by nonmathematicians! You will find that even a very simplified, highly qualitative molecular orbital theory can provide striking insights into structure and reactivity.
In Section 1.3, we constructed Lewis dot structures for molecules. Our next task is to elaborate on this theme to produce better models of the bonds that hold atoms together in molecules. We’ll need to consider how electrons act to bind nuclei together, and we’ll take as our initial example hydrogen (H2), the second simplest molecule.
PROBLEM 1.23 What is the simplest molecule? If H2 is the second simplest molecule, the answer to this question must be “H2 minus something.” What might the “something” be? The answer will appear farther along in the text, so think about this question for a while now.
We start with two hydrogen atoms, each consisting of a single proton, the nucleus, surrounded by an electron in the spherically symmetrical 1s orbital. In principle, the situation is this simple only as long as the two hydrogen atoms are infinitely far apart. As soon as they come closer than this infinite distance, they begin to “feel” each other. Remember: Wave functions do not vanish as the distance from the nucleus increases (see Fig. 1.6). In practice, we can ignore the influence of one hydrogen atom on the other until they come quite close together, but as soon as they do, the energy of the system changes greatly. As one hydrogen atom approaches the other, the energy of the two-atom system decreases until the two hydrogen atoms are 0.74 Å apart (Fig. 1.38). From this point the energy of the system rises sharply, asymptotically approaching infinity as the distance between the atoms approaches zero.
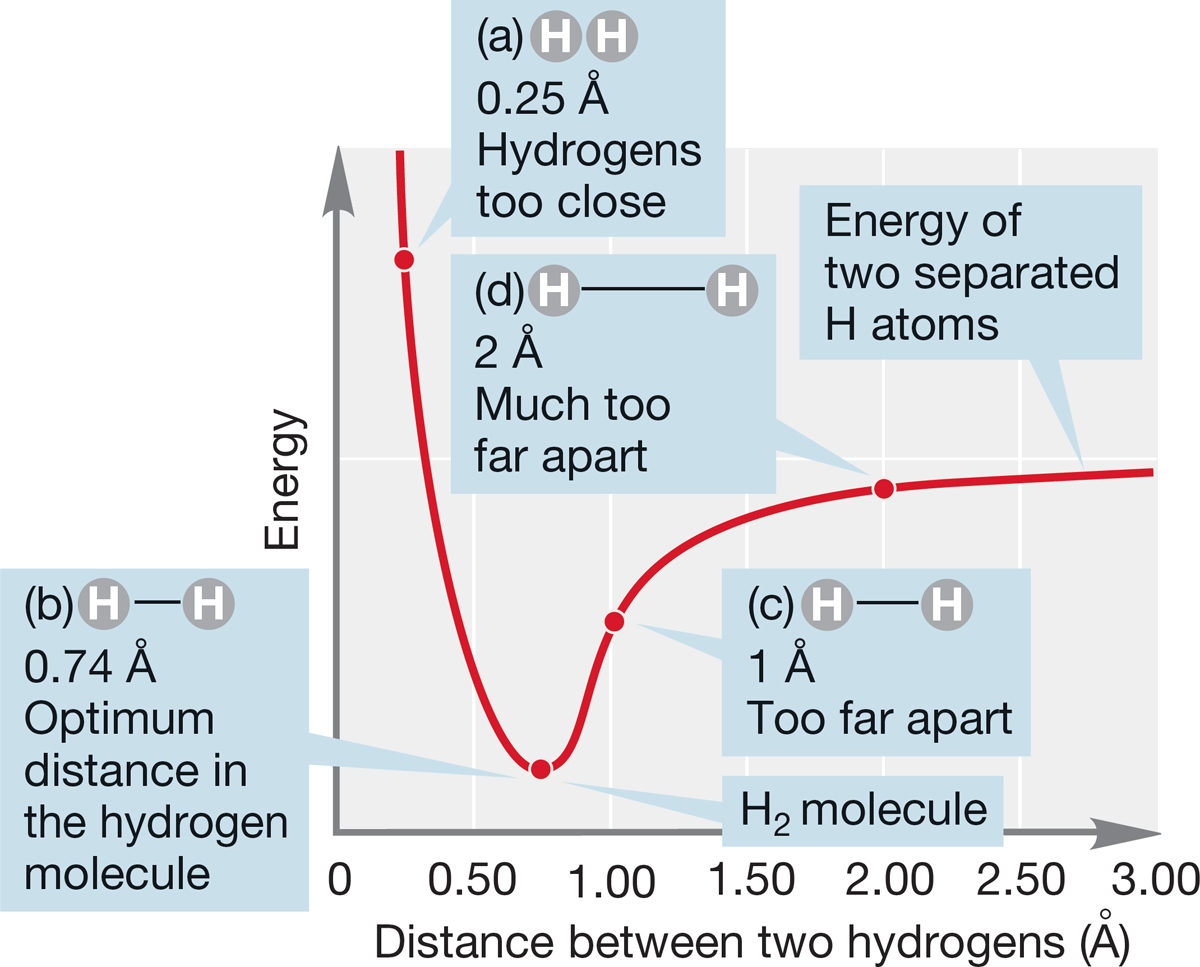
FIGURE 1.38 A plot of the energy for the hydrogen molecule (H2) as a function of the distance between the two hydrogen nuclei. The point of minimum energy corresponds to the equilibrium internuclear separation: the bond distance.
In the hydrogen molecule, two 1s electrons serve to bind the two nuclei together. The system H―H is more stable than two separated hydrogen atoms. In the molecule, the two negatively charged electrons attract both nuclei and hold them together. When the atoms approach too closely, the positively charged nuclei begin to repel each other, and the energy goes up sharply.
We begin our mathematical description of bonding by combining the two 1s atomic orbitals (symbol ψ) of the two hydrogen atoms to produce two new molecular orbitals. The first molecular orbital we will consider is called the bonding molecular orbital. Its symbol is Φbonding (this Greek letter is pronounced “fy”). We will use ΦB as a shorter notation for the bonding molecular orbital in this discussion. Wave function ΦB mathematically represents the bonding molecular orbital and results from a simple addition of the two atomic orbitals. It can be written as ψ(Ha, 1s) + ψ(Hb, 1s) = Φbonding = ΦB. This bonding molecular orbital is drawn in Figure 1.39, which shows that ΦB looks much like what one would expect from a simple addition of two spherical 1s orbitals.
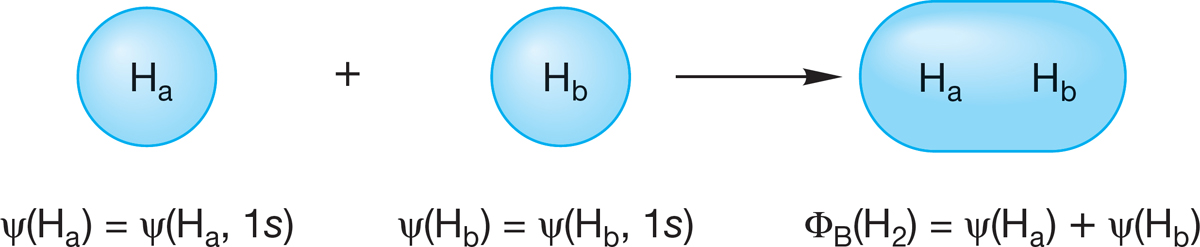
FIGURE 1.39 The bonding molecular orbital (ΦB) of H2.
CONVENTION ALERT
Minding Your Ψs and Φs
Many people use the Greek ψ for both atomic orbitals and molecular orbitals, but we will use Φ for molecular orbitals. Be careful in your other reading, though, because you will encounter situations in which ψ is used for all orbitals and even cases where Φ is used for atomic orbitals and ψ for molecular orbitals!
Because the bonding orbital ΦB is concentrated between the two nuclei (Fig. 1.39), two electrons in it can interact strongly with both nuclei. This attraction explains why the molecular orbital ΦB, in which the electron density is highest between the nuclei, is strongly bonding.
Quantum mechanics tells us an important principle: The number of wave functions (orbitals) resulting from the mixing process must equal the number of wave functions (orbitals) going into the calculation. Because we started by mixing two hydrogen atomic orbitals, a second molecular orbital must be formed. It is called an antibonding molecular orbital, Φantibonding or ΦA (Fig. 1.40), and results from the subtraction of one atomic orbital from the other to give ψ(Ha, 1s) − ψ(Hb, 1s) = Φantibonding = ΦA.

Molecular orbitals increase in energy as the number of nodes increases. A good analogy is the energy required to increase the number of nodes in a jump rope. This photo shows a rope with zero nodes in the bottom picture. A rope with one node requires more energy to generate, and a rope with two nodes requires even more.
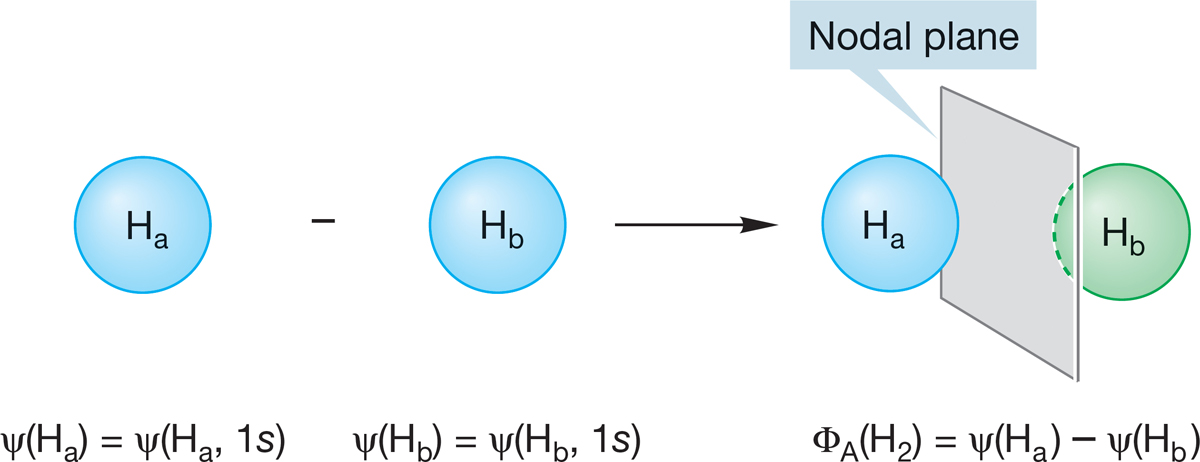
FIGURE 1.40 The antibonding molecular orbital of H―H (ΦA).
Electrons can occupy both bonding and antibonding molecular orbitals. An electron in a bonding orbital acts to hold the two nuclei together. As the name “antibonding” suggests, an electron in an antibonding orbital does just the opposite—it contributes to the dissociation of the two nuclei.
A third kind of molecular orbital exists; one in which electrons that occupy it have a neutral effect on the energy of the molecule. Such an orbital is called a nonbonding orbital. We will see some nonbonding orbitals when we come to molecules larger than H2.
By comparing Figures 1.39 and 1.40, you can see that in the antibonding molecular orbital ΦA, there is a nodal plane between the two hydrogen nuclei. Recall that a node is a region in which the sign of the wave function is zero. As we pass from a region where the sign of the wave function is positive to a region in which it is negative, the sign of Φ must go through zero. As noted earlier, the square of the wave function corresponds to the electron density, and if Φ is equal to zero, then Φ2 is also zero. Therefore, the probability of finding an electron at a node must be zero as well. Accordingly, when a pair of electrons occupies the antibonding molecular orbital of Figure 1.40, the two nuclei are poorly shielded from each other, and electrostatic repulsion forces the two positively charged nuclei apart.
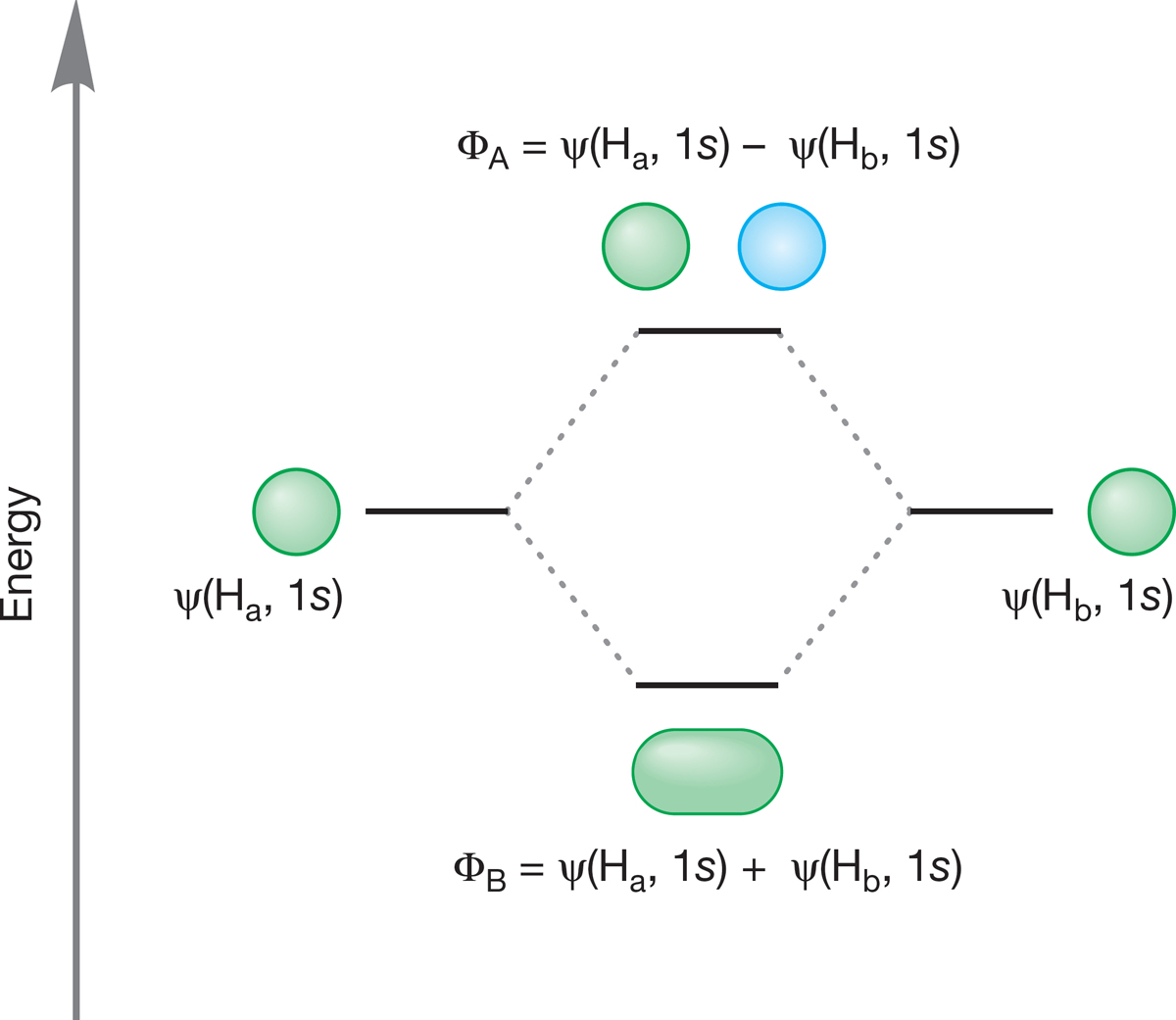
FIGURE 1.41 An orbital interaction diagram for H2—a graphical representation of the combination of two atomic 1s orbitals to form a new bonding and antibonding pair of molecular orbitals, ΦB and ΦA.
In summary, the combination of two hydrogen 1s atomic orbitals yields two new molecular orbitals, ΦB and ΦA. This idea seems intuitively reasonable. There are, after all, only two ways in which two 1s atomic orbitals can be combined to construct two new molecular orbitals. The signs of the wave functions can be either the same, as in the bonding orbital ΦB, or opposite, as in the antibonding orbital ΦA. One common analogy for this phenomenon is the jump rope, which has wavelike properties. If we start with a jump rope wave that has an amplitude of 3 meters and we add an in-phase wave of the same amplitude, then the result is a jump rope wave that has an amplitude of 6 meters. If, however, we start with the original amplitude and we subtract a wave (or add an out-of-phase wave) of the same amplitude, then we get a zero-amplitude wave. Subtracting the waves cancels them out.
Figure 1.41 shows a very simple and most useful graphic device for summing up the energy comparison between atomic orbitals and the molecular orbitals formed from mixing the orbitals. The graph is called an orbital interaction diagram, or an interaction diagram for short. The atomic orbitals (ψ) going into the calculation are shown at the left and right sides of the figure. For molecular hydrogen, these orbitals are the two equivalent hydrogen 1s atomic orbitals, which must be of the same energy. They combine in a constructive, bonding way (1s + 1s) to give the lower-energy ΦB and in a destructive, antibonding way (1s − 1s) to give the higher-energy ΦA. Constructive combination for wave functions means that they are in phase with each other. Destructive combination means that they are out of phase.
WORKED PROBLEM 1.24 Sketch the orbitals produced through the interaction of a carbon 2s atomic orbital overlapping end-on with a carbon 2p atomic orbital.

ANSWER The two atomic orbitals can interact in a bonding way (2s + 2p) or in an antibonding way (2s − 2p):
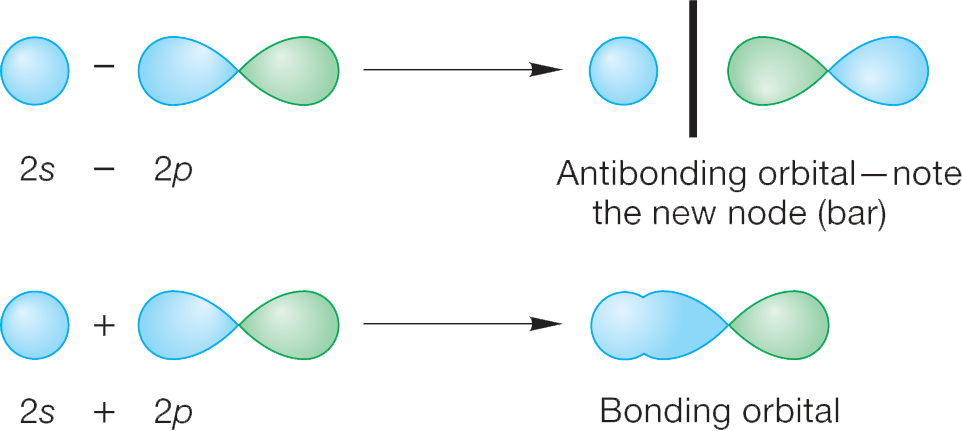
PROBLEM 1.25 The bond between two fluorine atoms in F2 can be viewed as resulting from the end-on interaction between the 2py orbital on each fluorine. Sketch the molecular orbitals produced through the interaction of two fluorine 2py atomic orbitals.
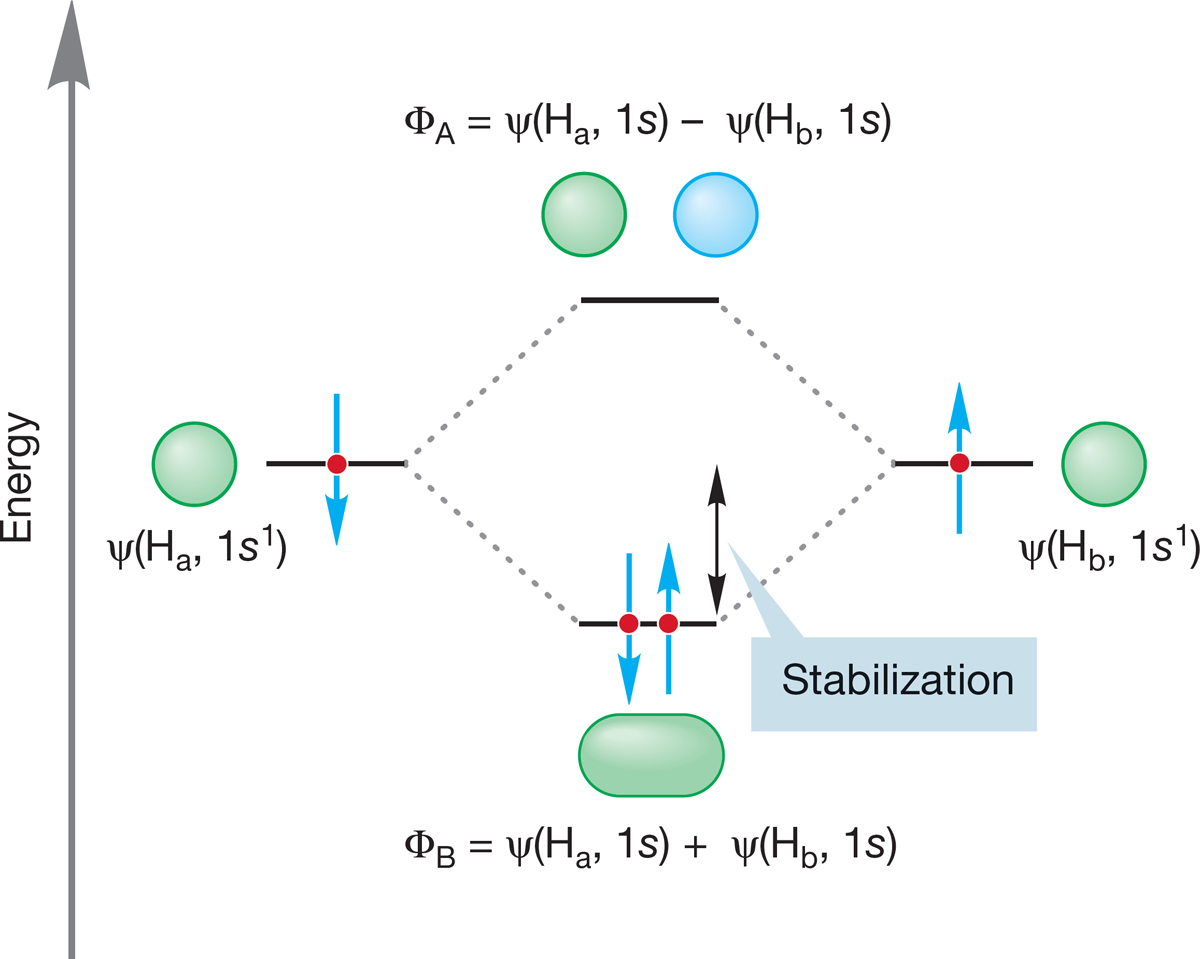
FIGURE 1.42 The electronic occupancy for the molecule H2.
Don’t fall into the trap of thinking there is a choice of forming just ΦB or just ΦA. Both must be formed from the interaction of the two atomic orbitals. In general, the rule is “n orbitals in produces n orbitals out.”
Note from Figure 1.41 that the orbital interaction diagram is constructed without reference to electrons. Only after the diagram has been constructed do we have to worry about electrons. But now let’s count them up and put them in the available molecular orbitals. In the construction of H2, each hydrogen atom brings one electron. In Figure 1.42, these electrons are placed in the appropriate 1s orbitals ψ(Ha) and ψ(Hb). The spins of the electrons are shown as paired, but we could also show them as parallel. In the H2 molecule, we put the two electrons into the lower-energy ΦB. The electrons must be paired because they are in the same orbital, and their spin quantum numbers must be different. The Pauli principle made this point earlier (p. 8). The antibonding molecular orbital (ΦA) is empty because we are dealing with only two electrons and they are both accommodated in the bonding molecular orbital.8
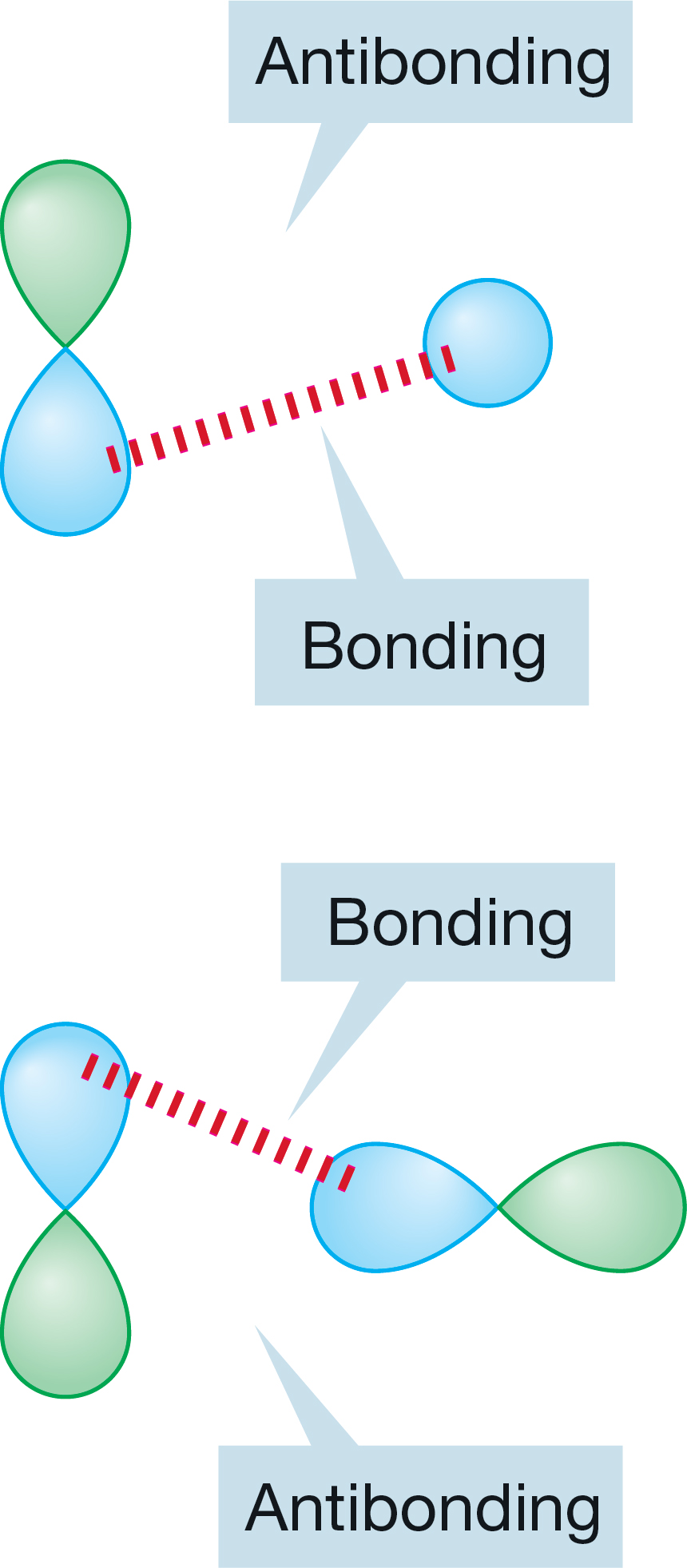
FIGURE 1.43 Two examples of noninteracting (orthogonal) orbitals.
So far, we have dealt only with mixing one atomic orbital with another atomic orbital. But it is also possible to mix a molecular orbital with another molecular orbital or an atomic orbital with a molecular orbital. Not all combinations of orbitals are productive. If two orbitals approach each other in such a way that the new bonding interactions are exactly balanced by antibonding interactions, there is no net interaction between the two orbitals, and no bond could form. Orbitals that do not mix are called orthogonal orbitals. Therefore, the way in which orbitals approach each other in space—how the lobes overlap—is critically important. Figure 1.43 shows two cases of atomic orbitals that are orthogonal to each other. As the orbitals approach each other, the number of bonding overlaps (shown with red dashed line) and antibonding overlaps are the same. The result is no net mixing. In each case, as the orbitals are brought together, the bonding interactions (blue–blue starting to overlap) are exactly canceled by the antibonding interactions (blue–green starting to overlap).
The following are guidelines for orbital construction:
1. The number of orbitals produced must equal the number of orbitals you begin with. If you start with n orbitals, you must produce n new orbitals. This is a way to check your work as you proceed.
2. Keep the process as simple as you can. Use what you know already, and combine orbitals in as symmetrical a fashion as you can.
3. The closer in energy two orbitals are, the more strongly they interact. At this simple (but useful) level of theory, you need mix only the pairs of orbitals closest in energy to each other.
4. The more in-phase (+/+ or −/−) overlap there is between mixing orbitals, the lower is the energy of the new bonding orbital. Out-of-phase overlap (+/−) leads to a new orbital of higher energy. Electrons in low-energy orbitals are more stable than electrons in higher-energy orbitals.
5. When two orbitals interact in a bonding way (wave functions for the two orbitals have the same sign), the energy of the resulting orbital is lowered; when they interact in an antibonding way (wave functions have different signs), the energy of the resulting orbital is raised.
6. When two orbitals interact, the only options for mixing are adding (in-phase mixing) or subtracting (out-of-phase mixing). When three orbitals interact, there will be three ways to mix the orbitals. With four orbitals there are four possible combinations, and so on.
7. To put new orbitals in order according to their energy, count the nodes. For a given molecule, the more nodes in an orbital, the higher it is in energy.
Stability and energy are connected. The lower the energy of an orbital, the greater the stability of an electron in it. A consequence of this stability is that the strongest bonds in molecules are formed by electrons occupying the lowest-energy molecular orbitals. Throughout this chapter, we will be taking note of what factors lead to low-energy molecular orbitals and thus to strong bonding between atoms.
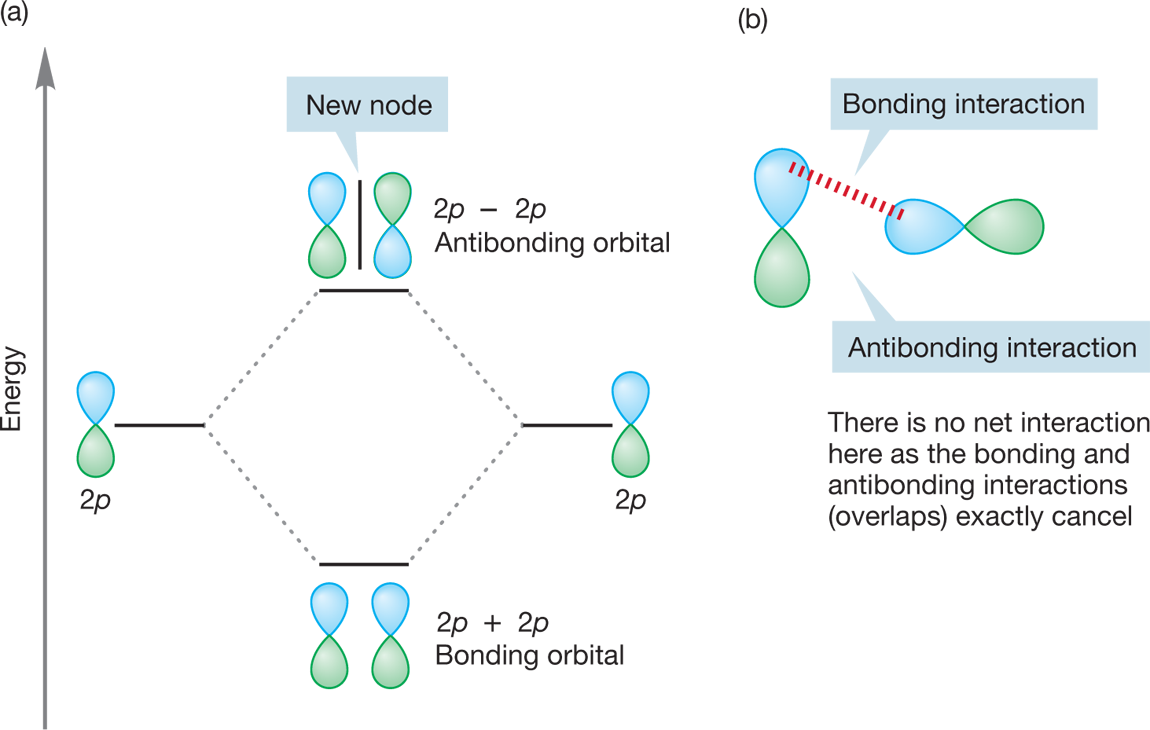
WORKED PROBLEM 1.26 Contrast the interactions between two 2p orbitals approaching in the two different ways shown below.
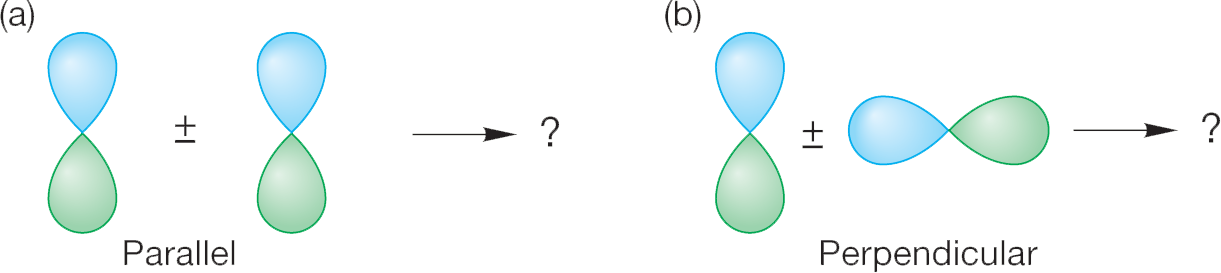
ANSWER (a) A pair of 2p atomic orbitals aligned parallel to each other and thus interacting side by side produces two new molecular orbitals, one bonding (2p + 2p) and one antibonding (2p − 2p). (b) The orbitals aligned perpendicular to each other produce no molecular orbitals because there is no net bonding or antibonding. The two possibilities exactly cancel, therefore there is no net interaction. In this case, the two orbitals are orthogonal.
Summary
Overlap of two atomic orbitals produces two new molecular orbitals, one bonding and the other antibonding. Two electrons can be accommodated in the lower-energy bonding molecular orbital. In this way, two atoms (or groups of atoms) can be bound through the sharing of electrons in a covalent bond.
8There can be no denying that the concept of an empty antibonding orbital is slippery! It makes physicists very uneasy, for example. Chemists see the empty orbital of Figures 1.41 and 1.42 as “the place the next electron would go.”