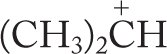7.7 Substitution, Nucleophilic, Unimolecular: The SN1 Reaction
7.7a Rate Law tert-Butyl bromide does not undergo an SN2 reaction when treated with the good nucleophiles listed in Table 7.5. The rate of the second-order SN2 displacement on tert-butyl bromide by hydroxide ion—or any nucleophile—is effectively zero. Yet, tert-butyl bromide does react with the much less powerfully nucleophilic molecule water to form the product of substitution, tert-butyl alcohol (Fig. 7.69).
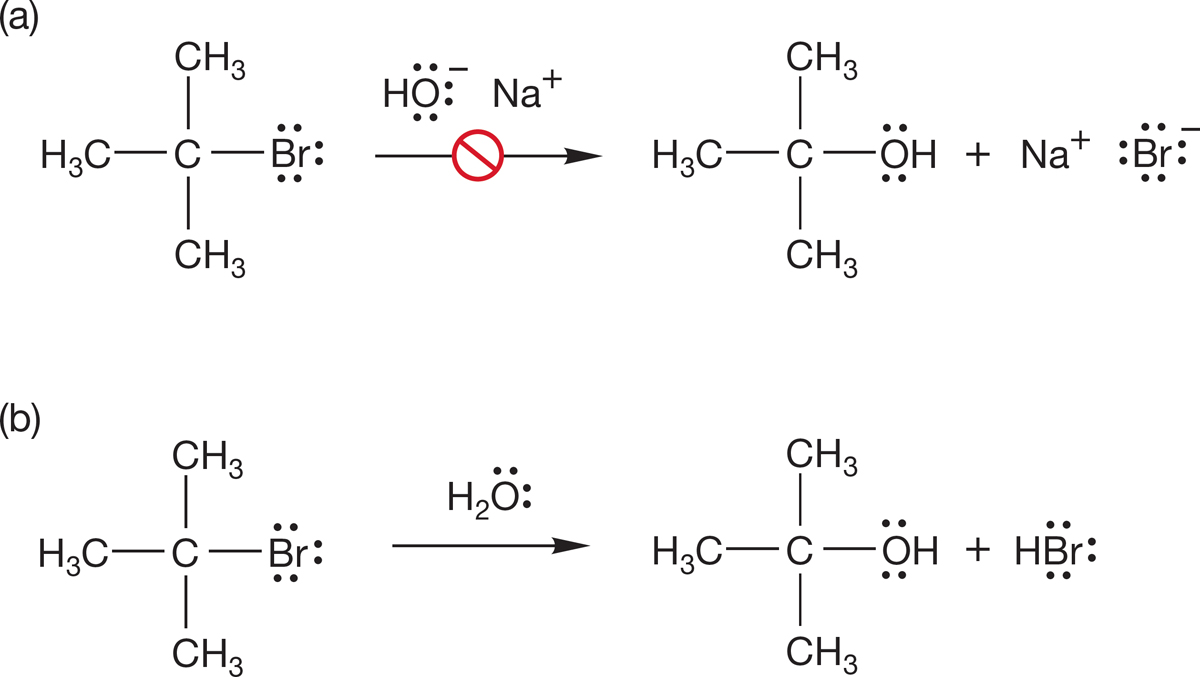
FIGURE 7.69 Despite the far greater nucleophilicity of hydroxide ion, the reaction (b) of tert-butyl bromide with water is successful in producing tert-butyl alcohol, whereas the reaction (a) with hydroxide ion is not, although a reaction between tert-butyl bromide and hydroxide does occur. See Problem 7.20.
PROBLEM 7.20 Although tert-butyl bromide does not give tert-butyl alcohol on reaction with hydroxide ion, an alkene product (C4H8) is produced. Suggest a structure for the product and an arrow formalism for this bimolecular reaction.
The first clue to what’s happening in Figure 7.69b comes from an examination of the rate law for the reaction. It turns out that the formation of tert-butyl alcohol in this reaction is a first-order process in which the concentration of added nucleophile is irrelevant to the rate. The rate law leads to the name Substitution, Nucleophilic, unimolecular, or SN1 reaction, where k is the rate constant, a fundamental constant of the reaction.
Rate = ν = k [tert-butyl bromide]
A reasonable mechanistic pathway for the SN1 reaction begins with the unimolecular ionization shown in Figure 7.70. The reaction continues as the carbocation is captured by the solvent, often water, as in Figure 7.70, in what is called a solvolysis reaction. Solvolysis simply means that the solvent, here water, plays the role of nucleophile in the reaction. Next, any base present, here likely to be water, can remove a proton (deprotonate the protonated alcohol) to give the alcohol itself (Fig. 7.70).

FIGURE 7.70 A schematic mechanism for the SN1 reaction. A slow ionization is followed by a relatively fast capture of the carbocation by a nucleophile, water in this case.
The energy versus reaction progress diagram for the SN1 reaction is more complicated than that for the SN2 reaction, because there are more steps than in the SN2 reaction. But the SN1 reaction is just a sequence of reversible reactions. Let’s look at the reaction of tert-butyl iodide with solvent water as an example. The first step is the formation of an intermediate carbocation. We expect this first reaction to be quite endothermic because a carbon–leaving group bond must be broken and ions must be formed. The high-energy point in this reaction, transition state 1, occurs as the carbon–iodine bond stretches (Fig. 7.71).
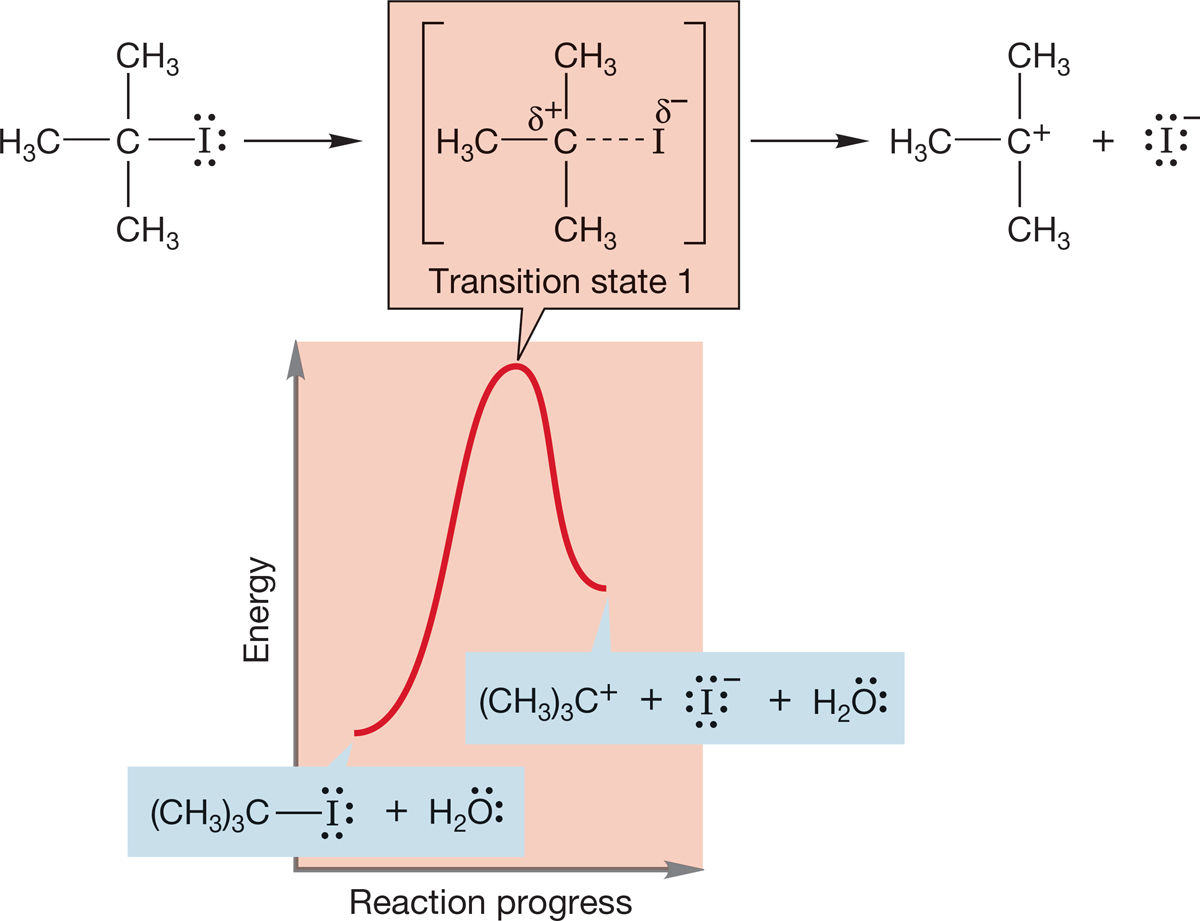
FIGURE 7.71 The first step in the SN1 reaction of tert-butyl iodide in water. The formation of the cation is highly endothermic.
The second step involves the reaction of the nucleophilic solvent water with the carbocation and is highly exothermic because a bond is made and none is broken. There is a second barrier, and therefore another transition state (transition state 2) for this second step of the reaction (Fig. 7.72).
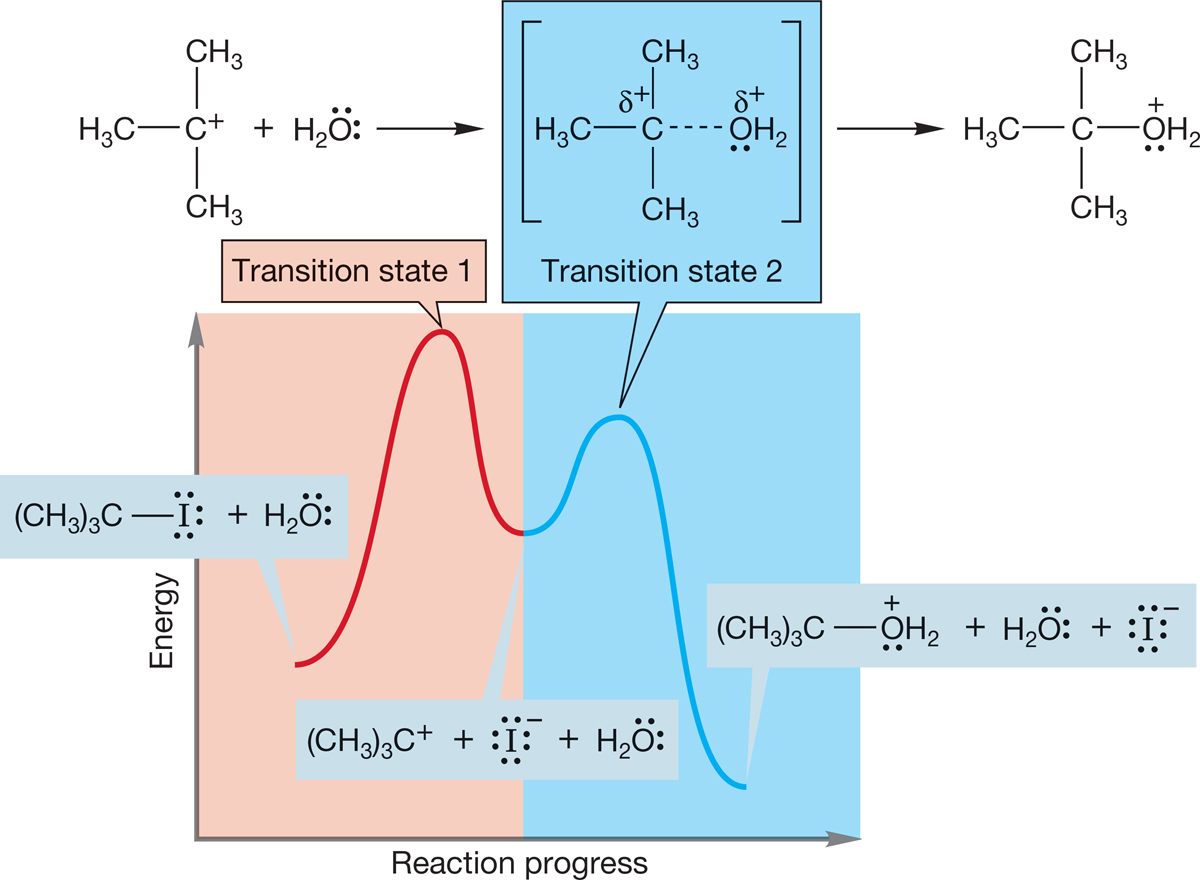
FIGURE 7.72 By contrast, the second step in this SN1 reaction, the capture of the cation by water, is highly exothermic. Transition state 2 is lower than transition state 1; therefore, capture of the carbocation by water is favored.
The third and final step in this particular SN1 reaction is removal of a proton from the oxonium ion by a base to give the ultimate product, tert-butyl alcohol. So there is a third barrier and a third transition state (Fig. 7.73).
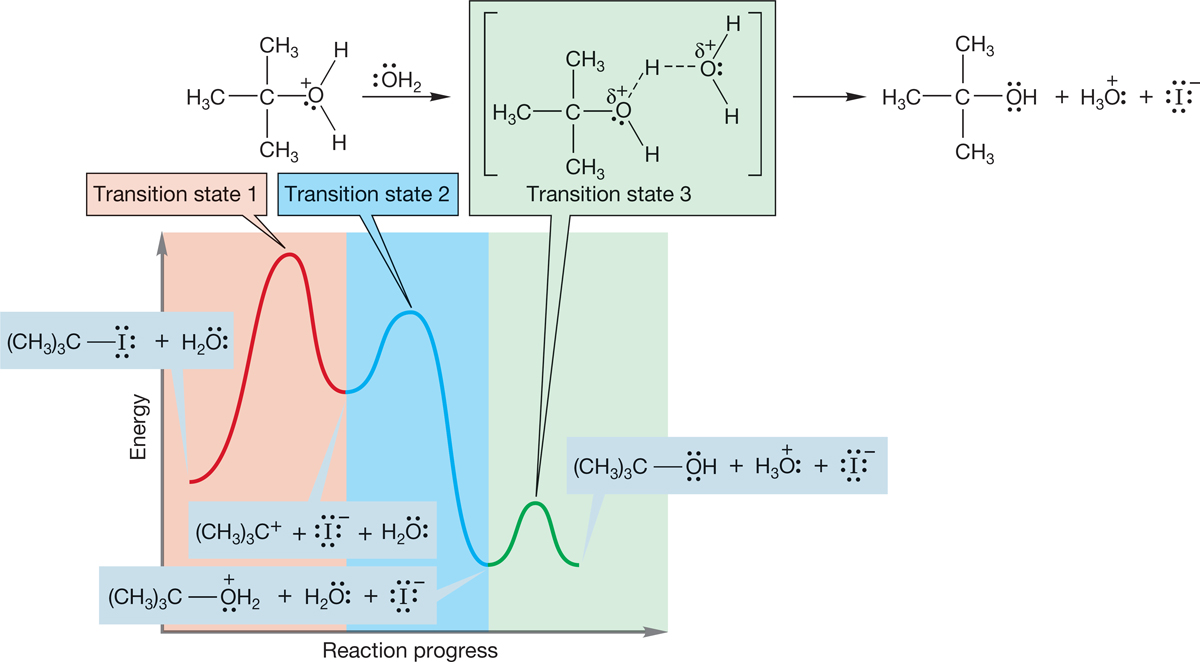
FIGURE 7.73 Transition state for the final step in this SN1 reaction.
PROBLEM 7.21 Draw the mechanism (arrow pushing) for the reaction shown. Draw an energy versus reaction progress diagram for the reaction.

There are six activation energies in the completed diagram for this SN1 reaction: three for the forward reactions and three for the reverse reactions (Fig. 7.74).
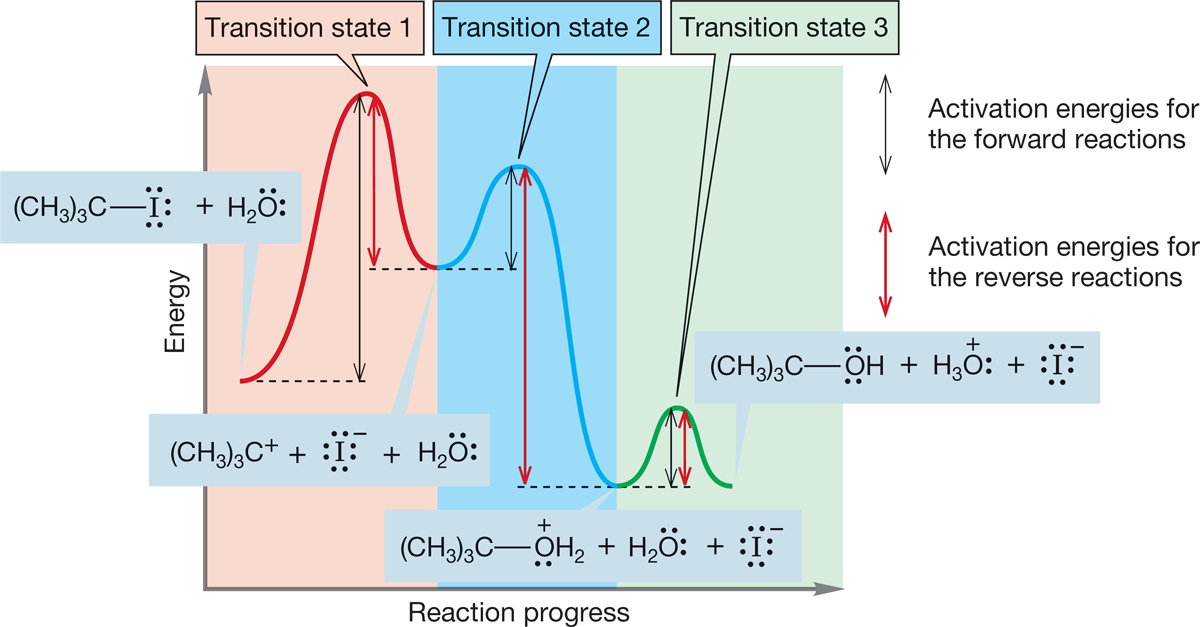
FIGURE 7.74 The three black double-headed arrows represent activation energies for the forward reactions, and the three red double-headed arrows represent activation energies for the reverse reactions.
Let us now concentrate on these energy barriers separating the various intermediates. The barriers are made up of the same quantities, enthalpy and entropy, that define the energy of any chemical species. Recall that ΔG° = ΔH° − TΔS°. Transition state theory assumes that we can treat a transition state as if it were a real molecule occupying a potential energy minimum. It is important to emphasize that it is not a minimum, however. It occupies an energy maximum and can never be bottled and examined as real molecules can. Nonetheless it has an energy, as indeed does every other point in the energy diagrams on the preceding pages. The energy of the transition state, and thus the height of the energy barrier in the reaction, can be calculated using Equation (7.8).

Remember: The double dagger (‡) simply indicates that we are referring to a transition state, not to an energy minimum. The energy barrier, ΔG‡, is the Gibbs free energy of activation, ΔH‡ is the enthalpy of activation, and ΔS‡ is the entropy of activation.
Clearly, the rate constant for any reaction will depend on the height of the barrier, and thus on ΔG‡. The theoretical study of reaction rates gives us the exact equation relating the rate constant k and ΔG‡ [Eq. (7.9)].
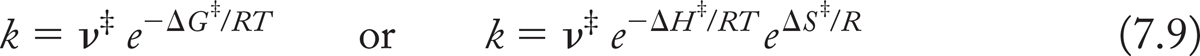
It is worth dissecting this equation a bit further. The quantity ν‡ is a frequency—its units are reciprocal seconds (s−1) in this case. In qualitative terms, ν is the frequency with which molecules with enough energy to cross the barrier actually do so. Thus, the rate constant k is equal to e−ΔG‡/RT (the fraction of molecules with enough energy to cross the barrier) times ν‡ (the frequency with which such molecules actually do cross the barrier).
Summary
Reaction rates are determined not by the relative energies of the starting material and product but by the height of the transition state separating them. Even though the transition state is an energy maximum, a transient species that cannot be isolated, its energy is determined by enthalpy and entropy factors, just as is the energy of any stable compound.
7.7b Stereochemistry of the SN1 Reaction If the SN1 reaction were as straightforward as suggested by Figures 7.70–7.72, what should we expect if we use an optically active starting material? The crucial intermediate in the reaction is the planar carbocation, an achiral molecule! Once the free, planar carbocation is formed, optical activity is inevitably lost. Addition of the nucleophile must take place at both faces of the cation, forming equal amounts of (R) and (S) product. This simple mechanism demands racemization, as Figure 7.75 shows.
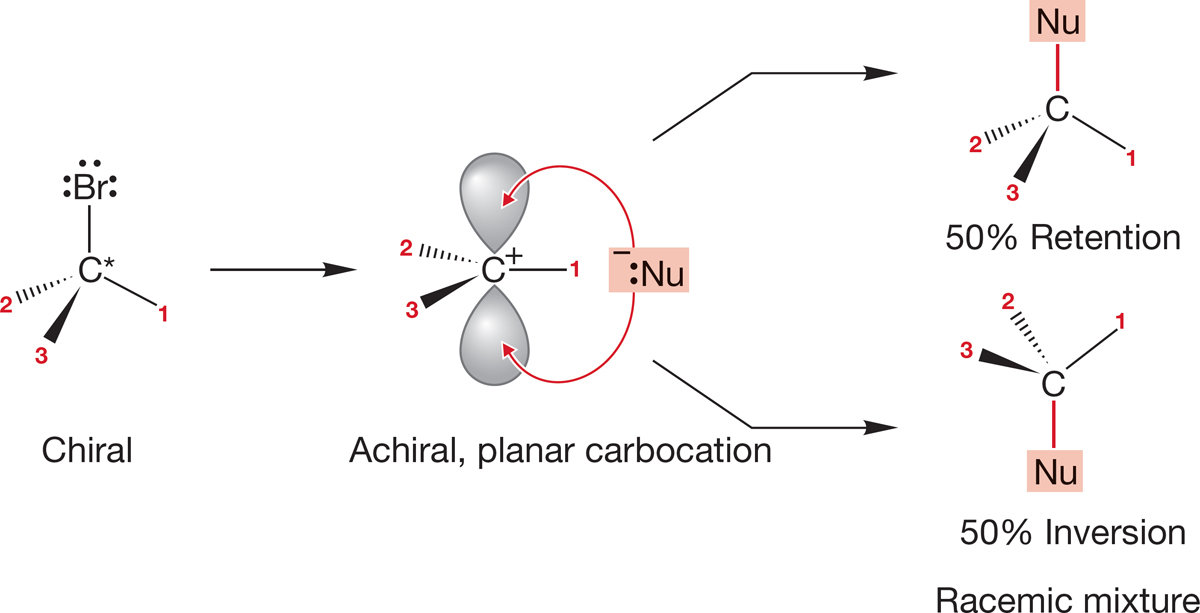
FIGURE 7.75 Loss of optical activity occurs as soon as the free, planar carbocation is formed. Addition of any nucleophile will occur equally at the two available lobes of the 2p orbital to give a racemic mixture of products.
Sometimes racemization is the actual result, and there is 50% inversion and 50% retention in the product. Usually, however, the stereochemical results are not so clean, and an excess of inversion is found. For example, the two optically active molecules of Figure 7.76 give 21% and 18% excess inversion in the SN1 reaction with water.
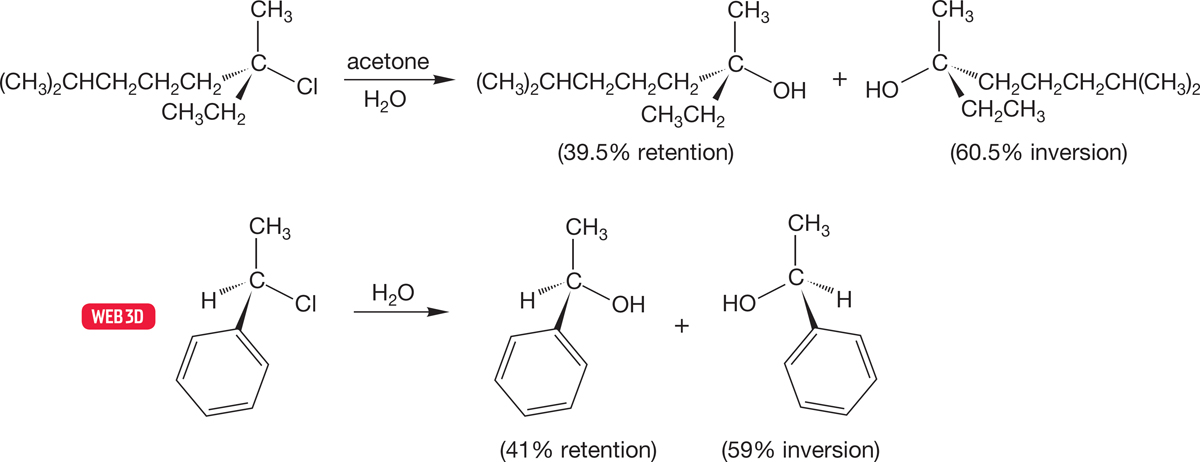
FIGURE 7.76 Incomplete racemization is often found in SN1 reactions. An excess of inversion is generally found.
Why is the product not racemic, and why is excess inversion (as opposed to retention) observed? These two questions are vitally important, as satisfactory answers must be found if we are not to be forced to abandon the proposed mechanism for the SN1 reaction. The answers turn out to be simple. In the mechanism outlined in Figures 7.70–7.74, we assumed that the leaving group had diffused away from the carbocation, leaving behind a symmetrical ion. What if reaction with solvent occurs before the leaving group diffuses completely away? What if reaction occurs with the pair of ions shown in Figure 7.77? The leaving group guards the side of the carbocation from which it departed and makes addition by solvent water more difficult at this “retention” side. The result is usually an excess of inversion.
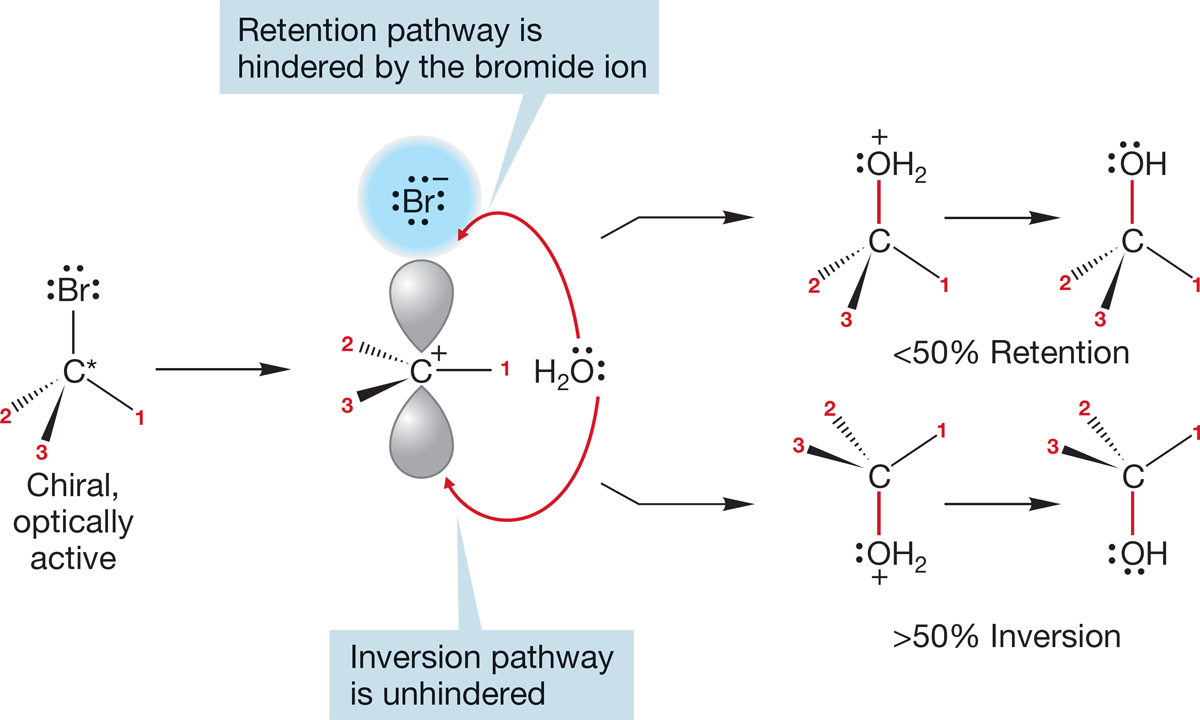
FIGURE 7.77 Until the leaving group, here bromide ion, completely diffuses away, it shields the carbocation along the retention pathway, and this results in an excess of inversion in most SN1 reactions.
PROBLEM 7.22 The second reaction of Figure 7.76 shows an SN1 reaction of a secondary halide. Explain why the SN1 reaction should be especially favorable for this secondary halide.
PROBLEM 7.23 Consider the role of solvent on the stereochemistry of the SN1 reaction shown in Figure 7.77. A more polar solvent favors racemization. Why?
7.7c Effects of Substrate Structure: The R Group The rate of the SN1 reaction is much greater for tertiary substrates than for secondary substrates, and simple primary alkyl and methyl halides do not react at all by the SN1 process. Our mechanistic hypothesis shows us why. If carbocation formation is the key step, only those compounds that can form relatively stable ions can react in SN1 fashion.
Modern measurements show that the stability of carbocations increases with substitution (p. 142). Table 7.7 shows the heats of formation of carbocations in the gas phase. Remember: The more positive the heat of formation of a species, the less stable the species is (p. 119). We can’t make too much of the quantitative data in Table 7.7 because these gas-phase measurements cannot take into account the effects of solvent, which are very large indeed. Nonetheless, the data do give a good qualitative picture of carbocation stability: Entries 5, 6, and 7 show that tertiary carbocations (three alkyl groups) are more stable than secondary ones (two alkyl groups), and secondary carbocations are more stable than primary ones (one alkyl group). The methyl cation (+CH3), with no alkyl groups, is the least stable of all. Do not confuse these relative stabilities with absolute stabilities. Carbocations are almost all very unstable species. A small atom such as carbon does not bear a positive charge with any grace, and a carbocation will react with available Lewis bases (e.g., halide ion) very quickly. Do not say, “The tert-butyl cation is very stable,” but rather, “For a carbocation, the tert-butyl cation is quite stable.”
TABLE 7.7 Heats of Formation for Some Carbocations
Entry |
Cation |
Substitution |
|
1 |
+CH3 |
Methyl |
261.3 (1094) Least stable |
2 |
+CH2CH3 |
Primary |
215.6 (902.7) |
3 |
+CH2CH2CH3 |
Primary |
211 (833) |
4 |
+CH2CH2CH2CH3 |
Primary |
203 (850) |
5 |
|
Secondary |
190.9 (799.3) |
6 |
|
Secondary |
183 (766) |
7 |
(CH3)3C+ |
Tertiary |
165.8 (694.2) Most stable |
PROBLEM SOLVING
 There are many reactions in which tertiary and secondary carbocations are intermediates, but no reactions take place for which a simple primary or methyl cation is required. These intermediates are simply too unstable. In practice, this instability means that when you find yourself writing a mechanism using a primary carbocation, think again, it’s almost certainly wrong.
There are many reactions in which tertiary and secondary carbocations are intermediates, but no reactions take place for which a simple primary or methyl cation is required. These intermediates are simply too unstable. In practice, this instability means that when you find yourself writing a mechanism using a primary carbocation, think again, it’s almost certainly wrong.
WORKED PROBLEM 7.24 We have again avoided (p. 142) a detailed discussion of why more-substituted carbocations are more stable than less-substituted ones.6 Nevertheless, you can now see the outlines of why this is so. Draw a three-dimensional picture of the ethyl cation. (Remember: The positively charged carbon and the three surrounding atoms are coplanar—this part of the ethyl cation is flat.) Now consider the overlap of one of the carbon–hydrogen bonds of the methyl group with the empty 2pz orbital. Is this interaction stabilizing? Why?
ANSWER Interactions between filled and empty orbitals are stabilizing. This fundamental tenet of chemistry can be applied in this case. If the filled orbital of the carbon–hydrogen bond overlaps with the empty 2p orbital of the carbocation, the result is the stabilizing interaction called hyperconjugation.
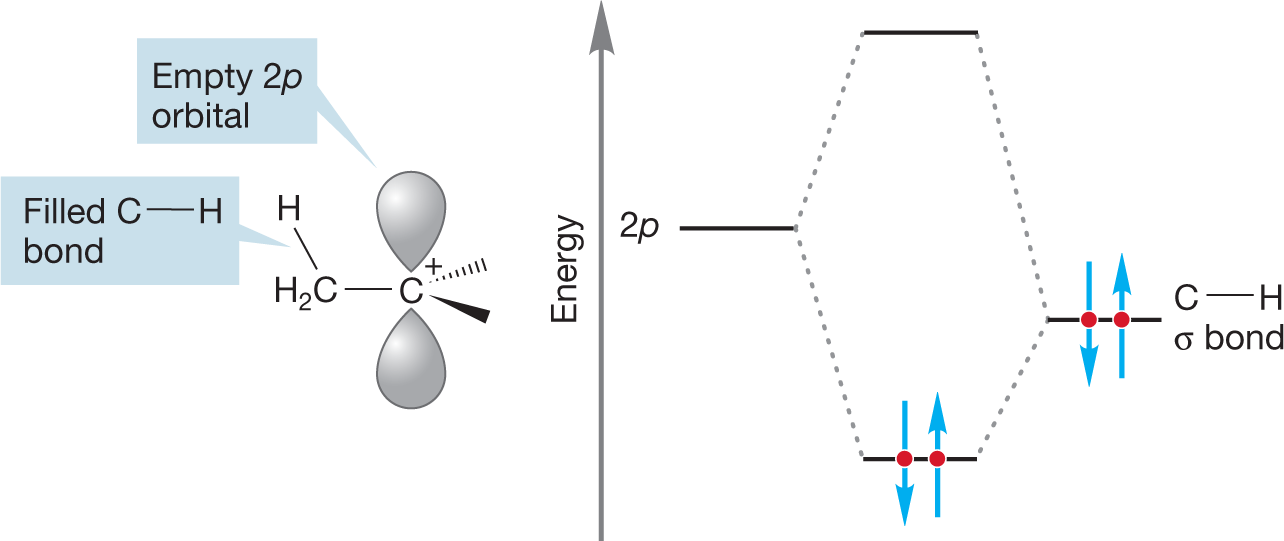
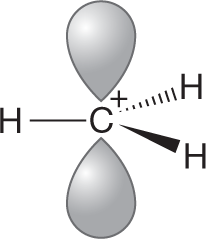
This interaction can occur only if the appropriate carbon–hydrogen bonds exist. The more alkyl groups, the more stabilization there is. For example, in the methyl cation, no such stabilization is possible because there are no alkyl groups to supply the needed C―H bonds.
So, tertiary compounds, which form the most stable, tertiary carbocations, commonly react through the SN1 mechanism, and methyl and primary compounds, which would have to form extremely unstable carbocations, do not. Naturally enough, secondary compounds react faster than primary ones in the SN1 reaction but more slowly than tertiary compounds (Fig. 7.78).
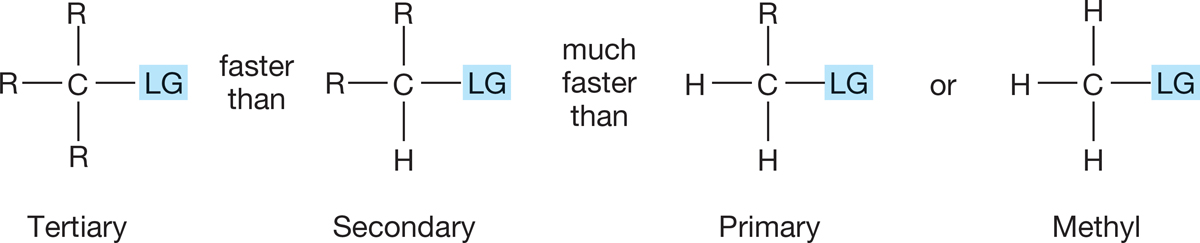
FIGURE 7.78 Relative reactivities in the SN1 reaction.
PROBLEM 7.25 The calculated heat of formation for (E)-CH3CH  CHCH2CHCH2+ is 227 kcal/mol (949 kJ/mol) and for (E)-CH3CH2CH
CHCH2CHCH2+ is 227 kcal/mol (949 kJ/mol) and for (E)-CH3CH2CH  CHCH2+ is 221 kcal/mol (926 kJ/mol). Draw the two cations showing the three-dimensional perspective and explain why one cation is more stable than the other.
CHCH2+ is 221 kcal/mol (926 kJ/mol). Draw the two cations showing the three-dimensional perspective and explain why one cation is more stable than the other.
7.7d Effects of the Nucleophile We have already seen that the nucleophile does not affect the rate of the SN1 reaction—the reaction is first order in substrate. Yet, the nucleophile does determine the product structure. Note the distinction between the rate-determining step (or rate-limiting step) and the product-determining step. For example, reaction of tert-butyl bromide in water containing a small amount of an added nucleophilic ion, such as cyanide, leads to substantial amounts of tert-butyl cyanide. Even though water is present as solvent and thus has an immense advantage over cyanide ion because of concentration, the more powerfully nucleophilic cyanide still competes. Cyanide is many times more reactive toward the carbocation than the solvent water is (Table 7.5, p. 295). In this reaction, the rate-determining step (the slow ionization) and the product-determining step (the faster capture of the intermediate ion by nucleophiles) are sharply separated (Fig. 7.79).
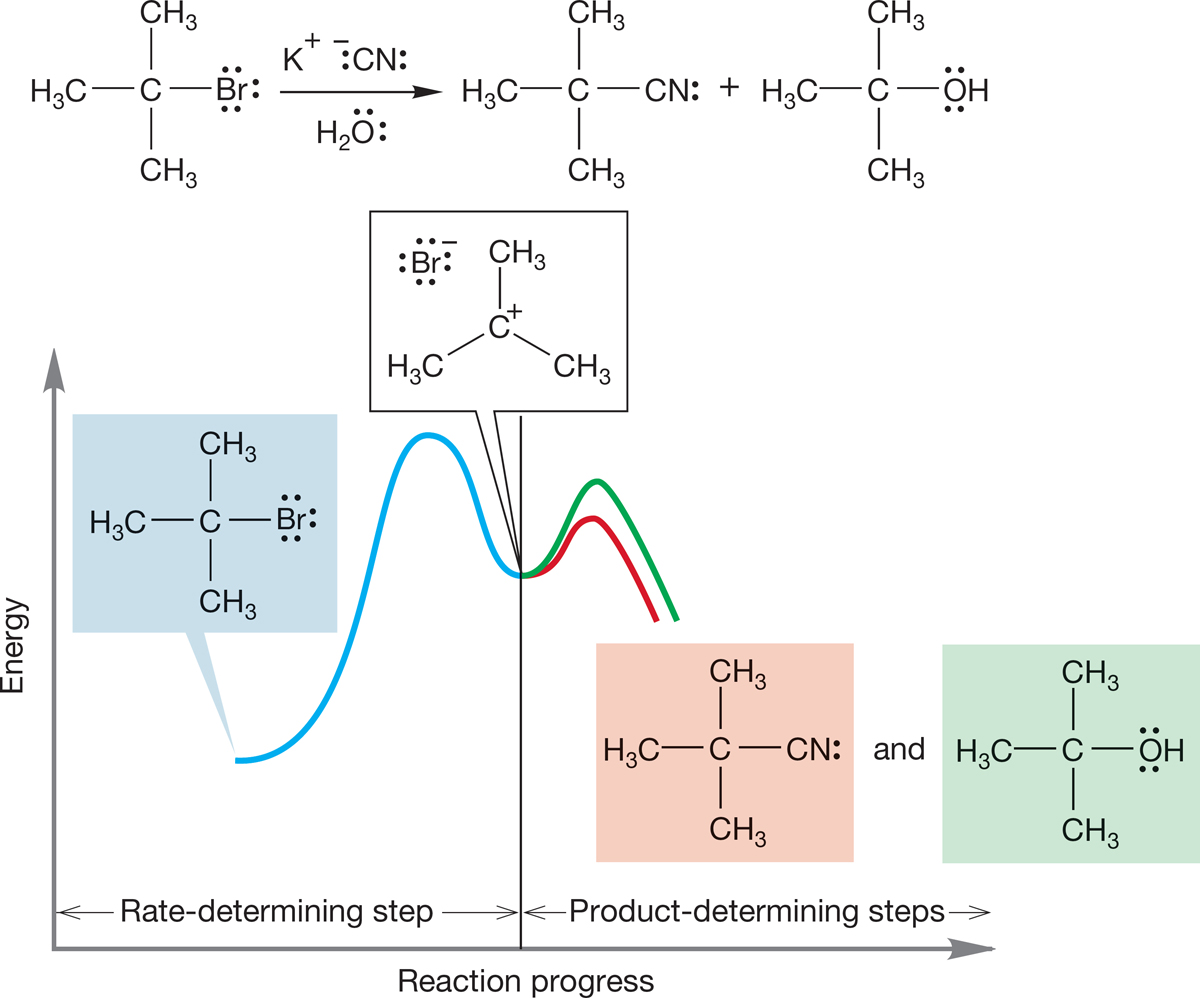
FIGURE 7.79 The rate-determining step and product-determining step are sharply distinguished in the SN1 reaction.
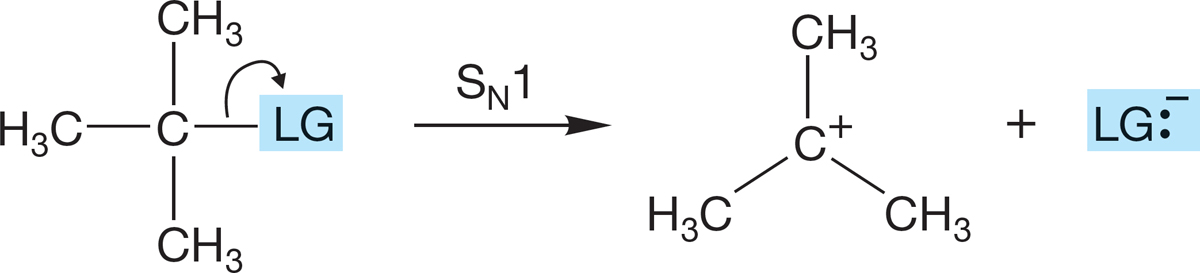
FIGURE 7.80 The rate of ionization is affected by the stability of the leaving group, LG:−. The more stable the leaving group, the faster is the ionization.
7.7e Effect of the Leaving Group The identity of the leaving group has a large influence on the rate of the SN1 reaction because the structure of the departing group affects the ease of ionization. We have already discussed how the structure—and hence stability—of the carbocation affects the rate of ionization, but obviously the stability of the negatively charged counterion LG:− is important as well. The more stable the anion, the more easily it is lost (Fig. 7.80). Some good and poor leaving groups are shown in Table 7.6 (p. 297).
7.7f Effect of Solvent For the SN2 reaction, the effect of solvent is rather complicated and depends on the charge type of the reaction. Some SN2 reactions are accelerated by a change to a more polar solvent; others are slowed down by such a change (p. 302). For most SN1 reactions, the situation is simpler. Ions are usually formed in the slow step of the reaction. In a polar solvent, represented by the dipole arrows in Figure 7.81, the charged species formed in the SN1 reaction are stabilized. A nonpolar solvent cannot stabilize as well. We can expect that the SN1 reaction will usually be favored by a polar solvent.
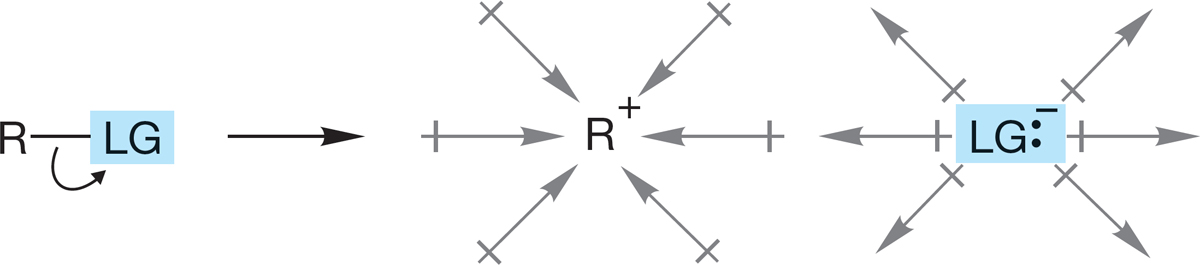
FIGURE 7.81 A polar solvent stabilizes the ions formed in an SN1 reaction.
6If avoiding the question drives you crazy, and we think it should at least make you a little uncomfortable, be sure to do this problem—the answer falls right out.
 , kcal/mol (kJ/mol)
, kcal/mol (kJ/mol)