1.11 Additional Problems
PROBLEM 1.35 Draw Lewis dot structures for the following compounds:
(a) CH3NO2 (nitromethane, used for fuel in stock car racing)
(b) CH2 CHCl (vinyl chloride used to make polyvinyl chloride, also known as PVC)
CHCl (vinyl chloride used to make polyvinyl chloride, also known as PVC)
(c) CH3CO2H (acetic acid, the acid in vinegar)
(d) HOSO2OH (sulfuric acid, H2SO4, the world’s most widely used industrial chemical)
See the inside front cover for structures, if you don’t know them.
PROBLEM 1.36 Draw two resonance structures for each of the compounds in the previous problem. Show the arrow formalism for interconversion of the resonance forms for each compound.
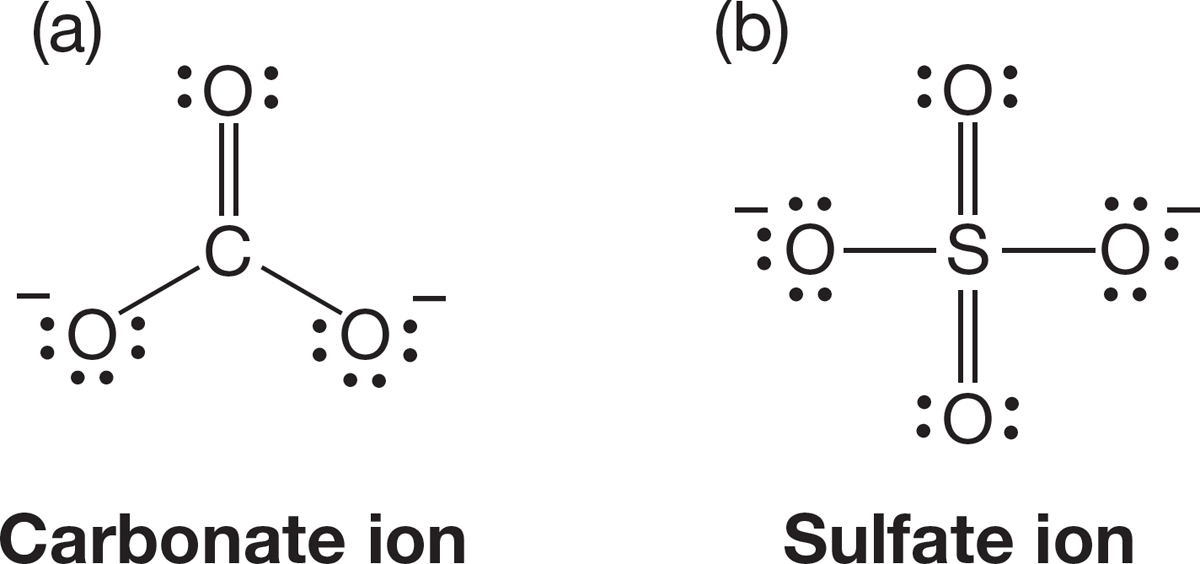
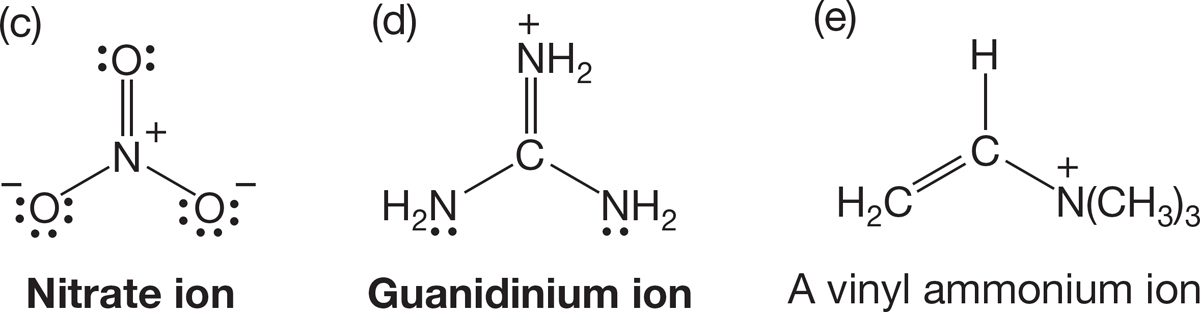
PROBLEM 1.37 Use the arrow formalism to write structures for the resonance forms contributing to the structures of the following ions:
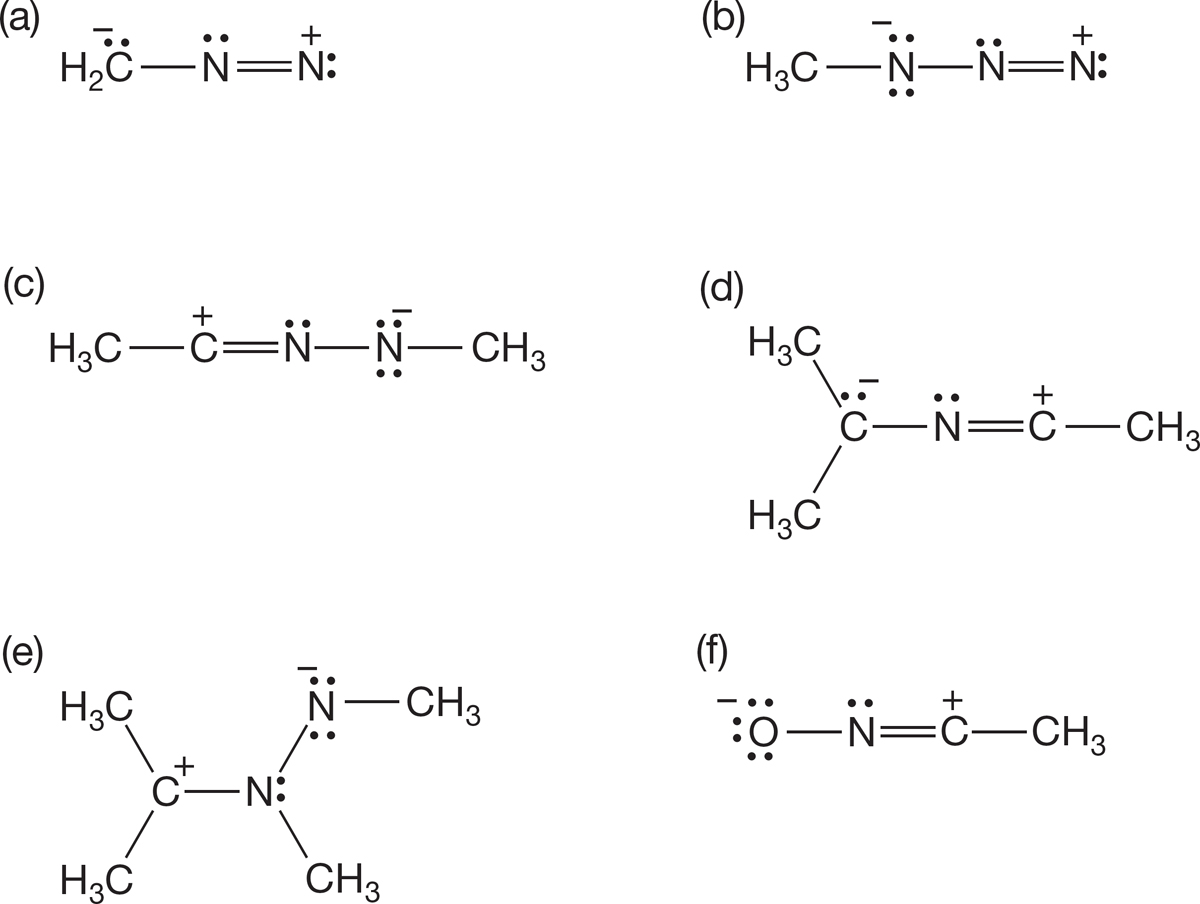
PROBLEM 1.38 Use the arrow formalism to draw three additional resonance structures for each of the following molecules:
PROBLEM 1.39 Draw three resonance structures for each of the following:
(a) −CH2NO2
(b) CH3CO2CH3
(c) −CH2CO2−
(d) HOSO2O−
PROBLEM 1.40 The curved arrow formalisms shown in this problem are wrong. Redraw them correctly.
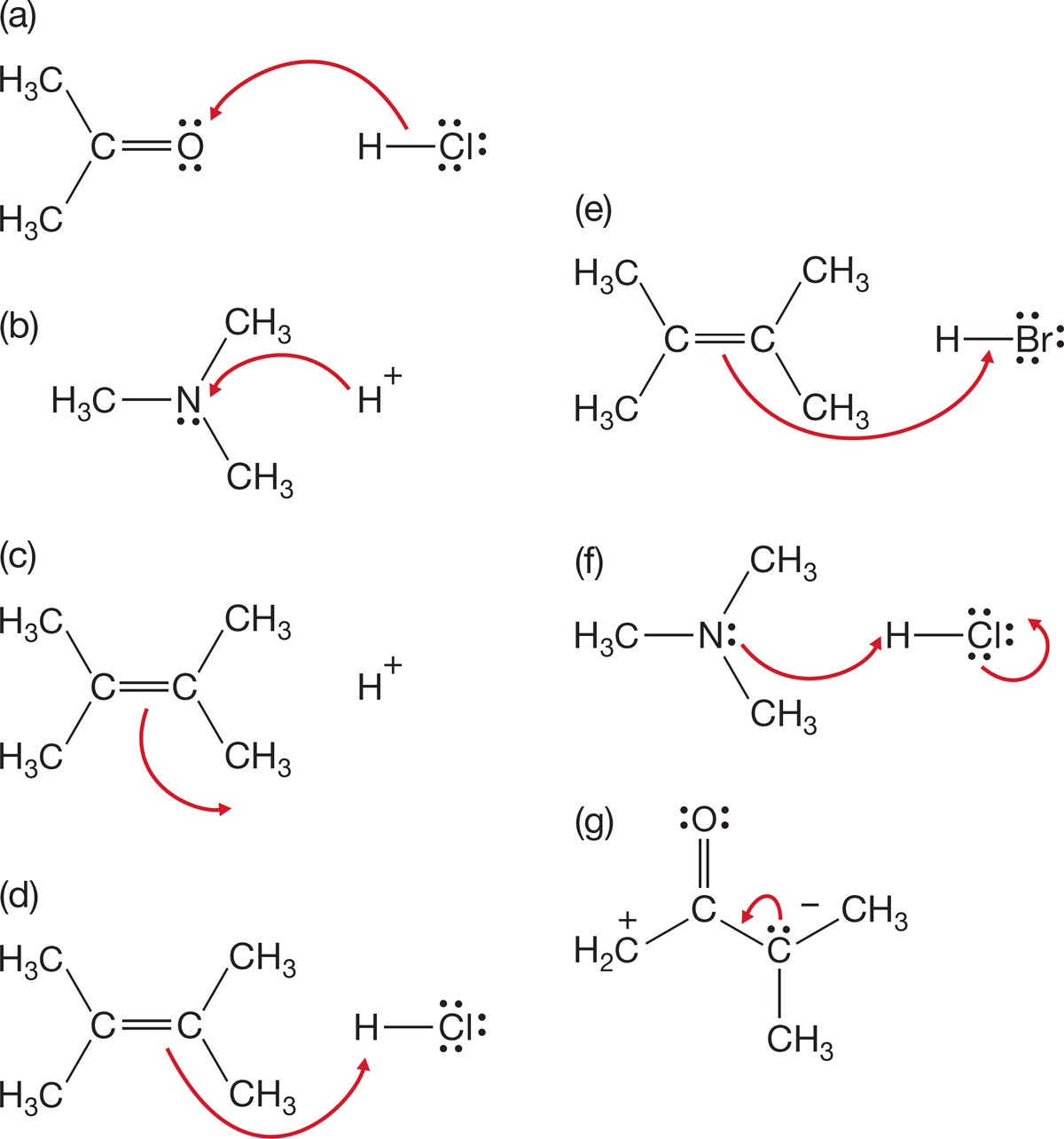
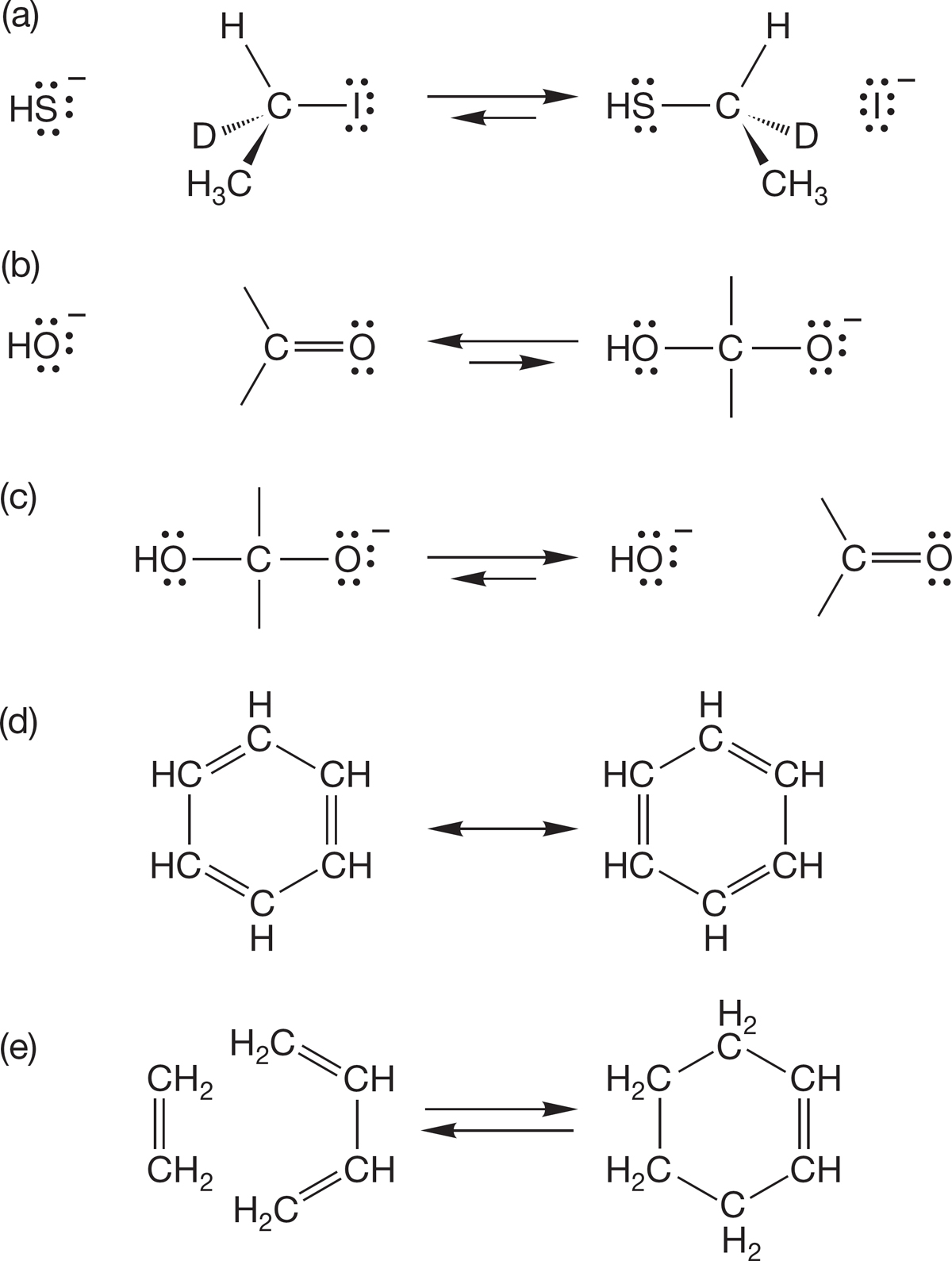
PROBLEM 1.41 Add the arrows to the following equilibria:
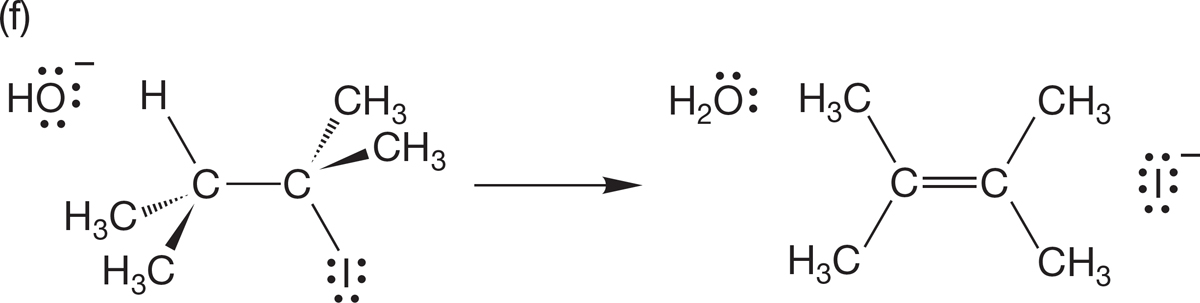
PROBLEM 1.42 Draw resonance forms for the following cyclic molecules:
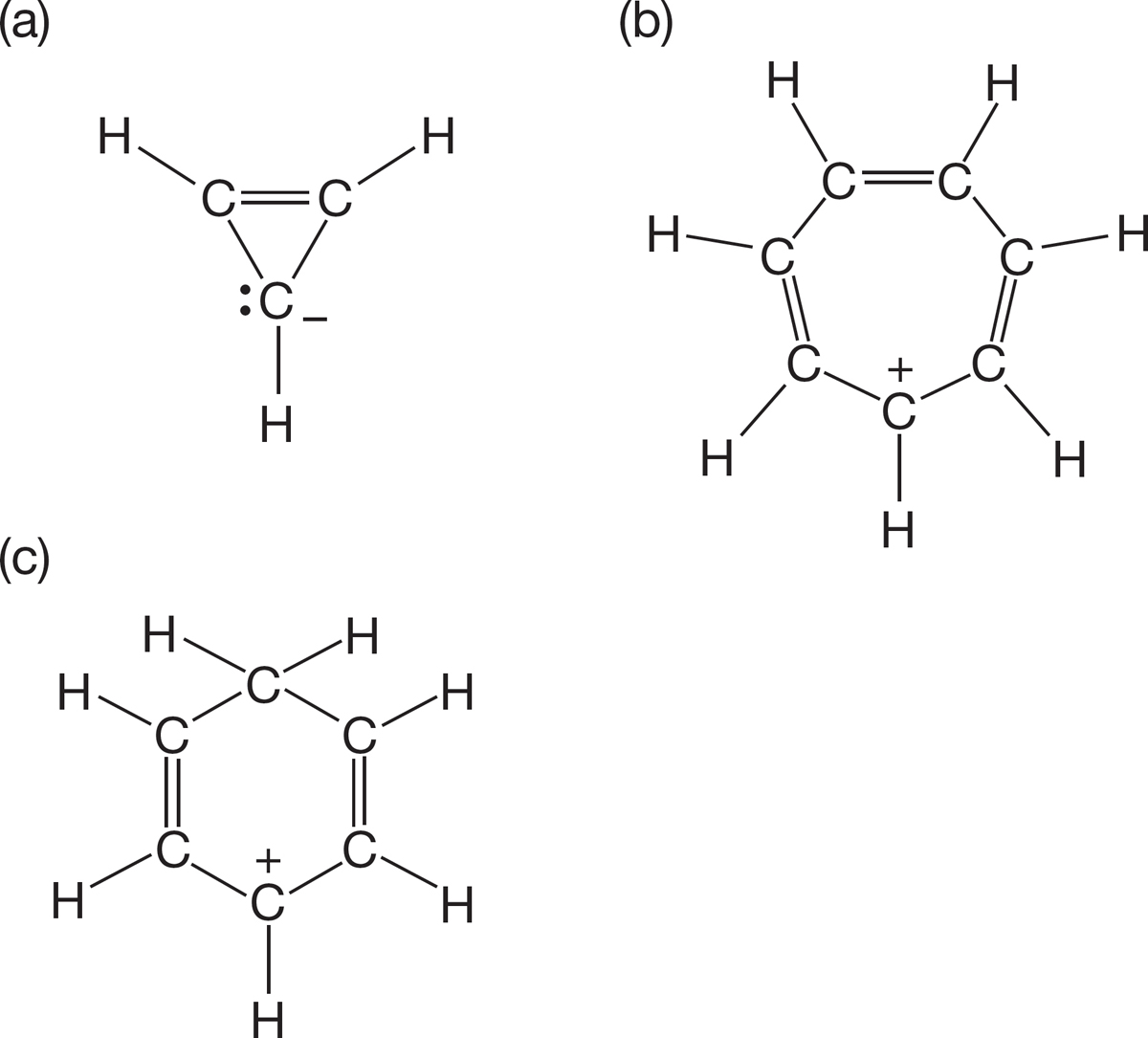
PROBLEM 1.43 Draw resonance forms for the following acyclic molecules:
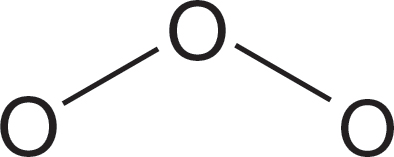
PROBLEM 1.44 Ozone (O3) resembles the molecules in Problem 1.38. These days it has a rather bad press, as it is present in too small an amount in the stratosphere and too great an amount in cities. Write a Lewis “dot” structure for ozone and sketch out contributing resonance forms. Write one neutral resonance form. Be careful with this last part; the answer is tricky.
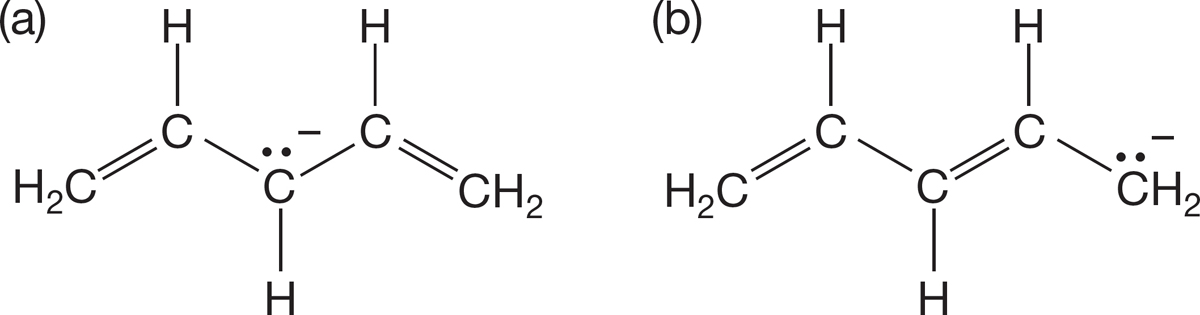
PROBLEM 1.45 Draw two resonance structures for each of the compounds shown below.
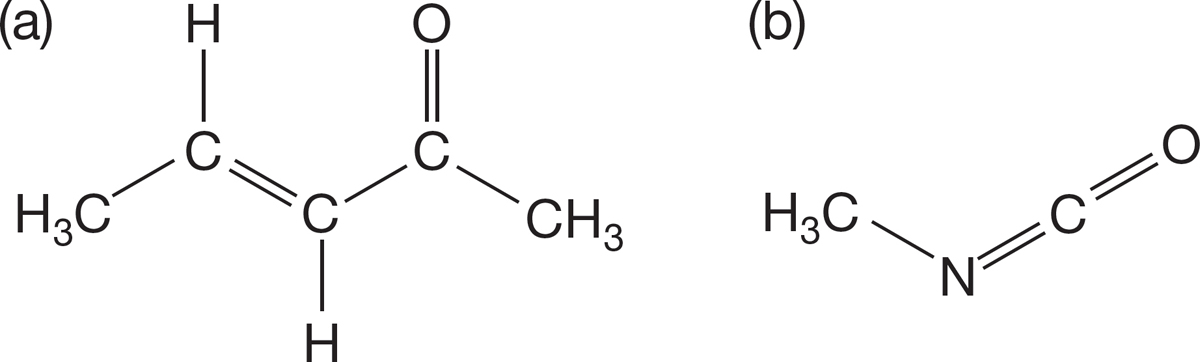
PROBLEM 1.46 Show the curved arrow formalisms for interconverting the forms you drew in Problem 1.45.
PROBLEM 1.47 Which “resonance structure” (b or c) does not contribute to the molecule  (a)? Why doesn’t it contribute?
(a)? Why doesn’t it contribute?

PROBLEM 1.48 Add charges to the following molecules where necessary:

PROBLEM 1.49 Add charges to the following molecules where necessary:
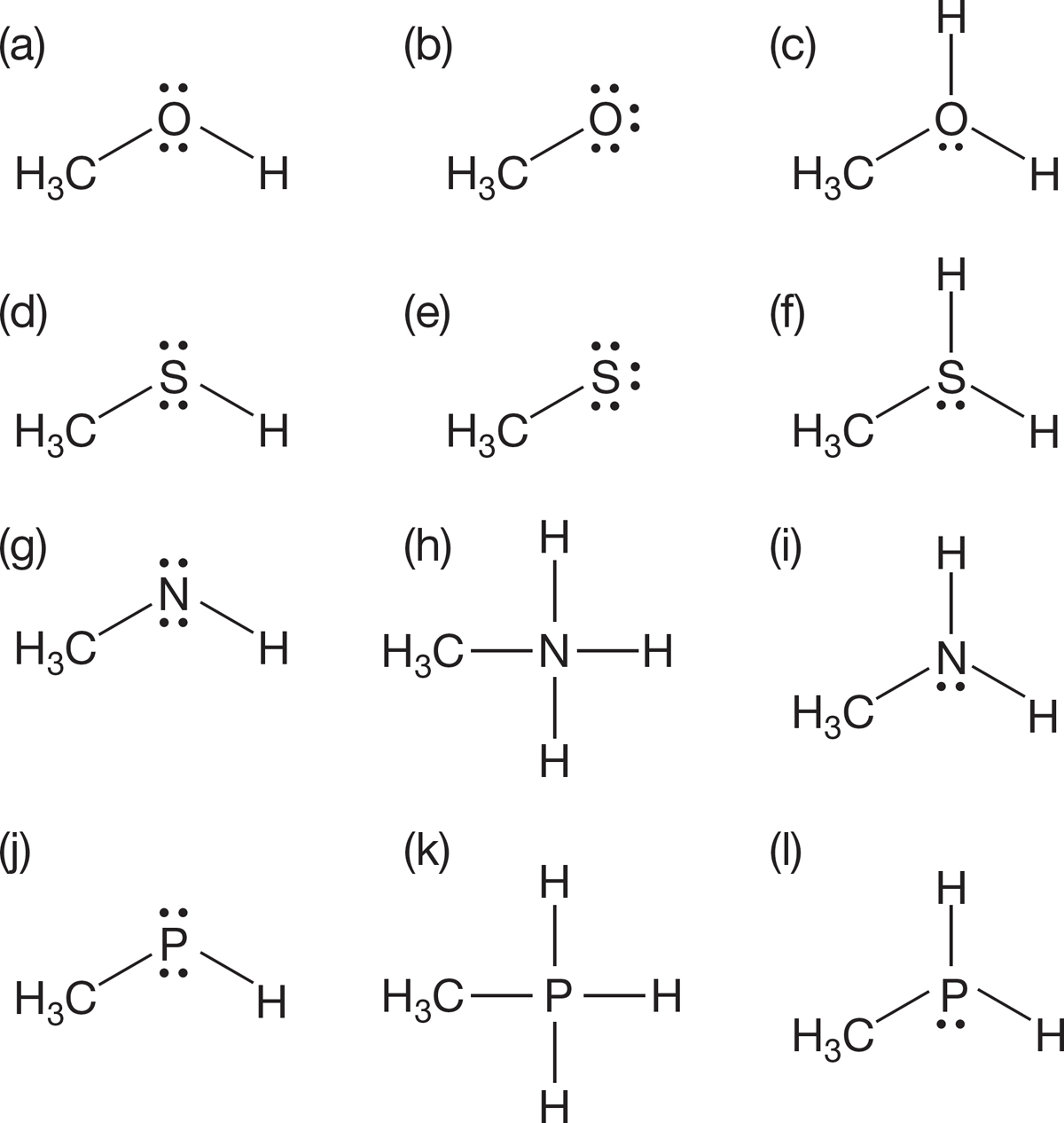
PROBLEM SOLVING
What to do with a “strange” atom like S or P in Problem 1.49? Organic chemistry is largely, but not entirely, confined to the second row of the periodic table, so what do you do when you encounter some atom that is not in the second row? First, don’t panic—if you know the second row of the periodic table, you can deal with most of the “strange” atoms you will see. But you do have to know a few more things. First, P, Si, and S sit right below N, C, and O. Second, the halogens form a series: F, Cl, Br, I. If you know the electron counts for the second-row elements, you don’t have to go through the more elaborate counting necessary to deal with elements in subsequent rows. If neutral trivalent N has a pair of nonbonding electrons, so does P. If neutral divalent O has two pairs of electrons, so does S. Therefore, HOH and HSH are related. If tetravalent N is positively charged as in H4N+, so is tetravalent P as in H4P+.
We’ll deal later with atoms further down in the periodic table.
PROBLEM 1.50 Determine the formal charge, if there is one, for each of the nitrogens in the following molecules:
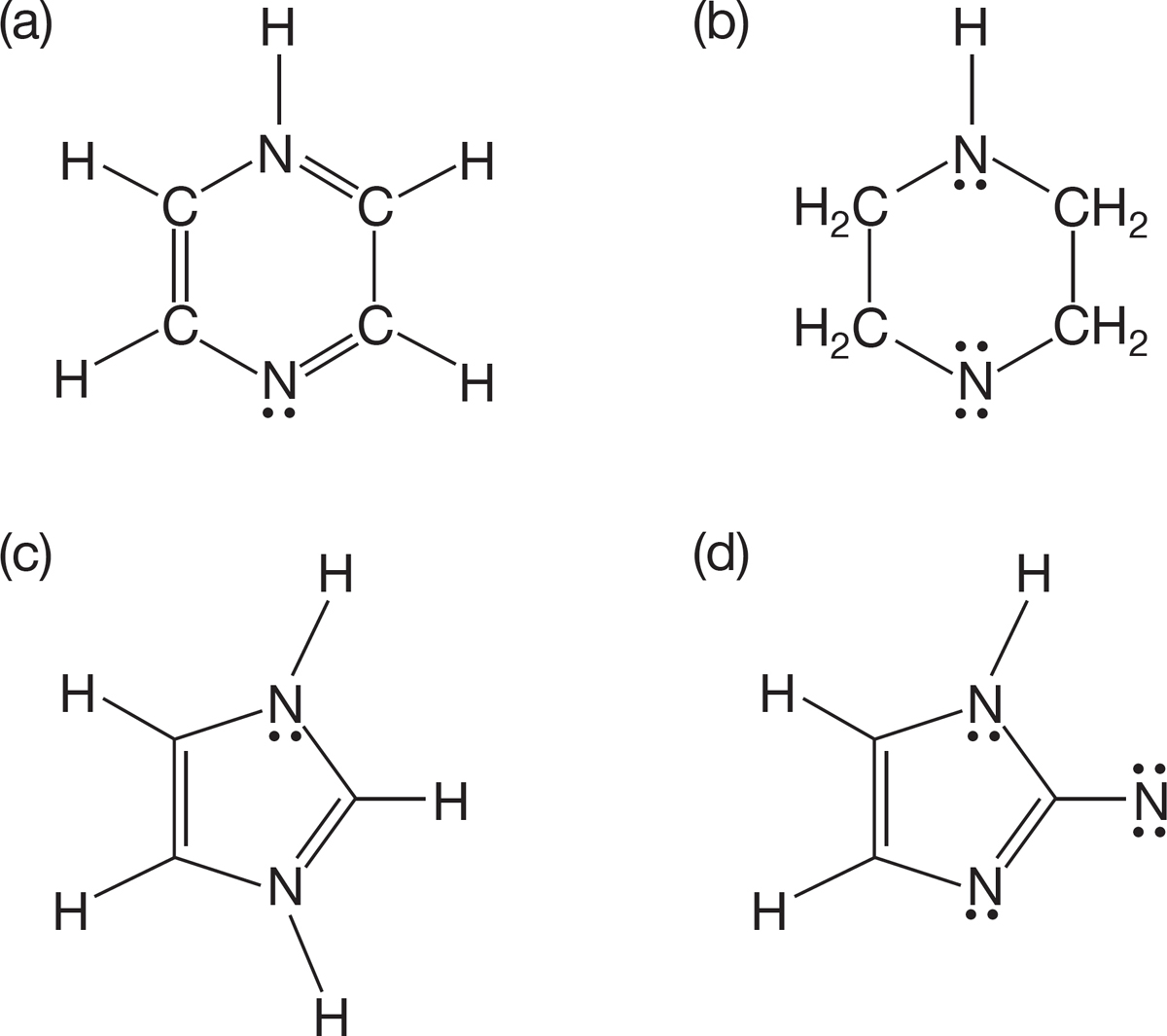
PROBLEM 1.51 Determine the formal charges, if any, for the molecules shown below.
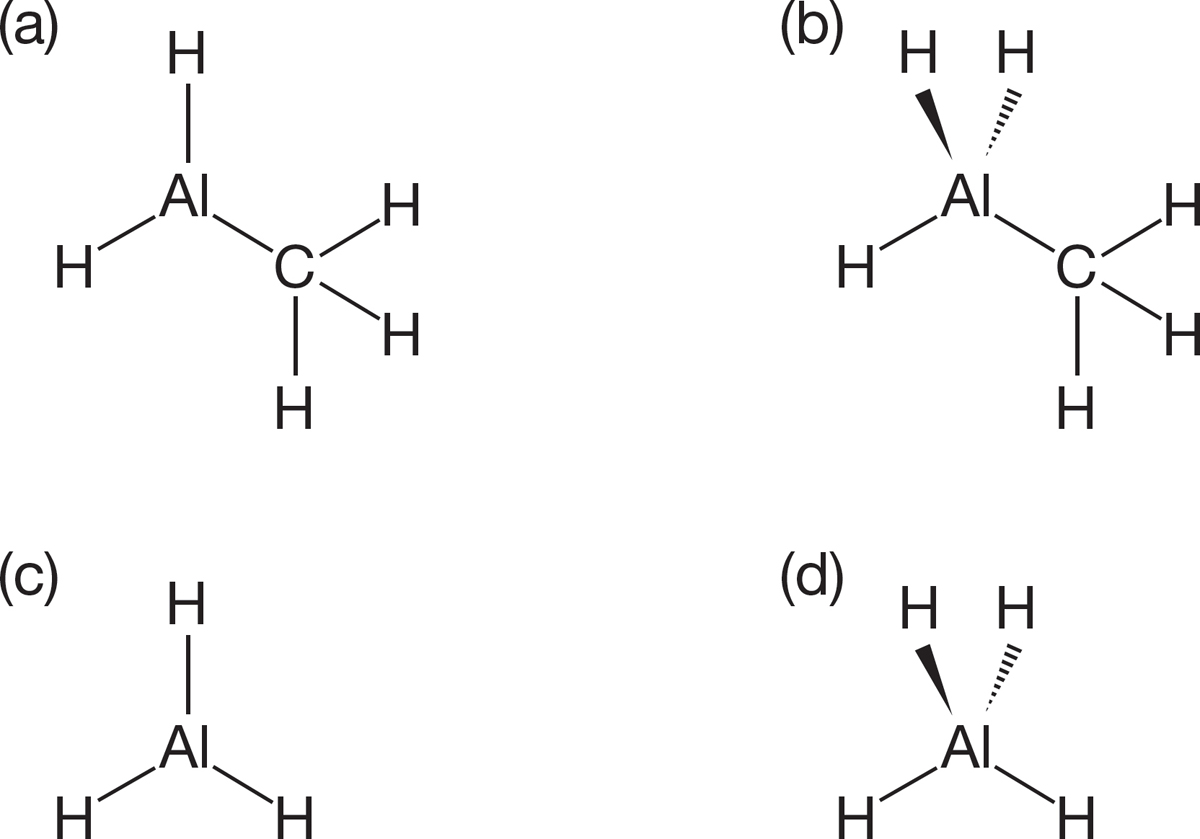
PROBLEM 1.52 Write Lewis dot structures for the neutral diatomic molecules F2 and N2. In F2, there is a single bond between the two atoms, but in N2 there is a triple bond between the two atoms.
PROBLEM 1.53 Atomic carbon can exist in several electronic states, one of which is (of course) lowest in energy and is called the “ground state.” Write the electronic description for the ground state and at least two higher-energy, “excited states.”
PROBLEM 1.54 Write the electronic configurations for the following ions:
(a) Na+
(b) F−
(c) Ca2+
PROBLEM 1.55 Write the electronic configurations for the atoms in the fourth row of the periodic table, 19K through 36Kr. Hint: The energy of the 3d orbitals falls between the energies of the 4s and 4p orbitals. Don’t worry about the ml designations of the 3d orbitals.
PROBLEM 1.56 Write electronic configurations for the valence electrons of 14Si, 15P, and 16S. Indicate the spins of the electrons in the 3p orbitals with a small up or down arrow.
PROBLEM 1.57 There is an instrument, called an electron spin resonance (ESR) spectrometer, that can detect “unpaired spin.” In which of the following species would the ESR machine find unpaired spin? Explain.
(a) O
(b) O+
(c) O2−
(d) Ne+
(e) F−
PROBLEM 1.58 For the Lewis structure of carbon monoxide shown below, first verify that both the carbon and the oxygen atoms are neutral.
Second, indicate the direction of the dipole moment in this Lewis structure:

As you have just shown, on the basis of this Lewis structure carbon monoxide should have a substantial dipole moment. In fact, the experimentally determined dipole moment is very small, 0.11 D. Draw a second resonance structure for carbon monoxide, verify the presence of any charges, and indicate the direction of any dipole in this second resonance form. Finally, rationalize the observation of only a very small dipole moment in carbon monoxide.
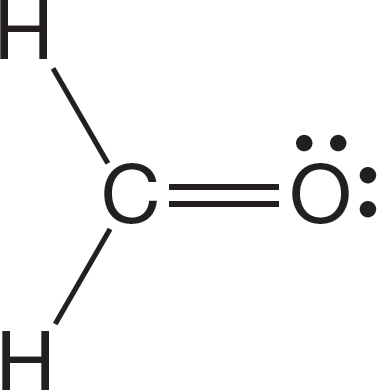
PROBLEM 1.59 Would you expect formaldehyde, shown below, to have a greater dipole moment than carbon monoxide (see Problem 1.58)? Why or why not?
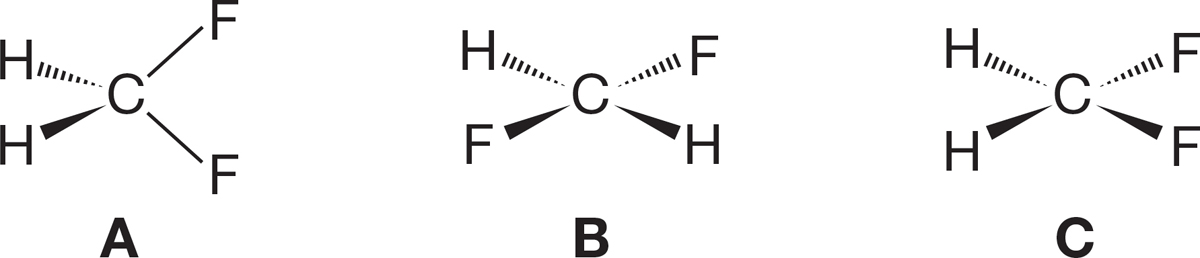
PROBLEM 1.60 Consider three possible structures for methylene fluoride (CH2F2), one tetrahedral (structure A), the others flat (structures B and C). Does the observation of a dipole moment in CH2F2 allow you to decide between structures A and B? What about structures A and C?
PROBLEM 1.61 Draw the arrow formalism for the homolytic cleavage of Br2. Draw the arrow formalism for the heterolytic cleavage of Br2.
PROBLEM 1.62 While wandering in an alternative universe, you find yourself in a chemistry class and, quite naturally, you glance at the periodic table on the wall. It looks (in part) like this:
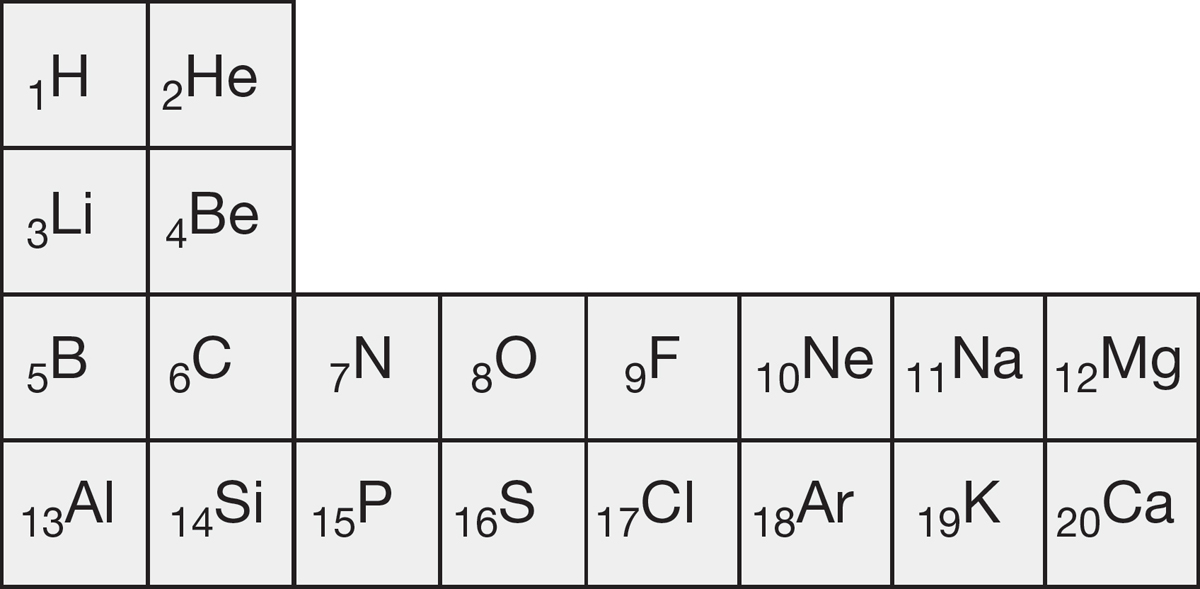
Deduce the allowed values for the four quantum numbers in the alternative universe.
PROBLEM 1.63 Indicate whether the following reactions are exothermic or endothermic. Estimate by how much. Use Table 1.10 (p. 40) and 66 kcal/mol for the “double” part of C C.
C.
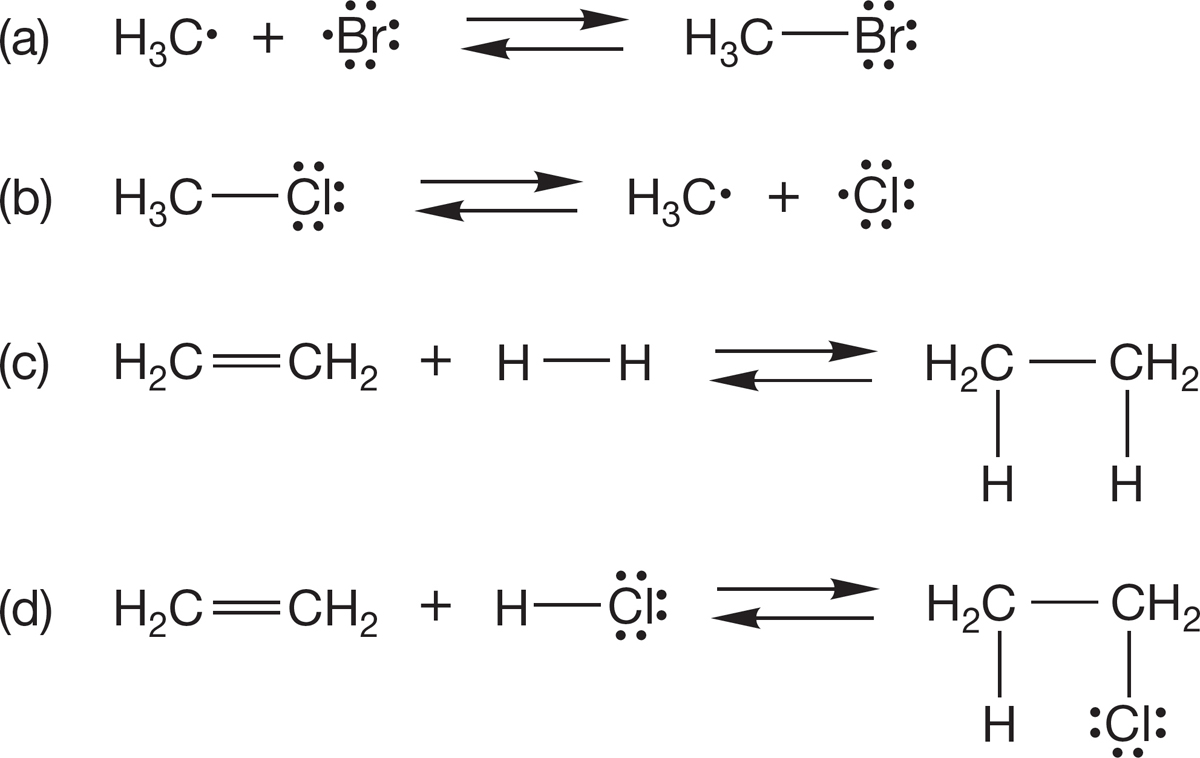
PROBLEM 1.64 Let’s extend our discussion of H―H a little bit to make the orbitals for the molecule linear HHH. Use the molecular orbitals for H2 and the 1s atomic orbital of H. Place the new H in between the two hydrogen atoms of H―H. Watch out for net-zero (orthogonal) interactions!
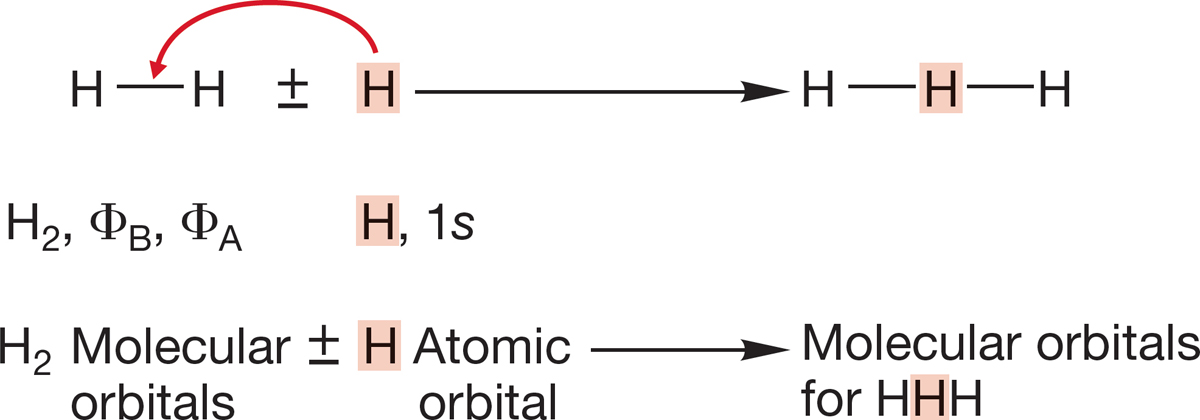
(a) How many orbitals will there be in linear HHH?
(b) Use the molecular orbitals of H2 and the 1s orbital of hydrogen to produce the molecular orbitals of linear HHH. Sketch the new orbitals.
(c) Order the new orbitals in energy (count the nodes).
The following molecular orbital problems are more challenging than the earlier ones and may be fairly regarded as “special topics.” Nonetheless, they do provide some remarkable insights, and for those who like orbital manipulation, they will actually be fun. Just remember the “rules” outlined on p. 36.
PROBLEM 1.65 Make a set of molecular orbitals very much like the ones you made for linear HHH in Problem 1.64, but this time use 2p orbitals, not 1s orbitals. Place one 2p orbital between the other two. Use the molecular orbitals 2p + 2p and 2p − 2p that you constructed in Problem 1.26. Order the new orbitals in energy.
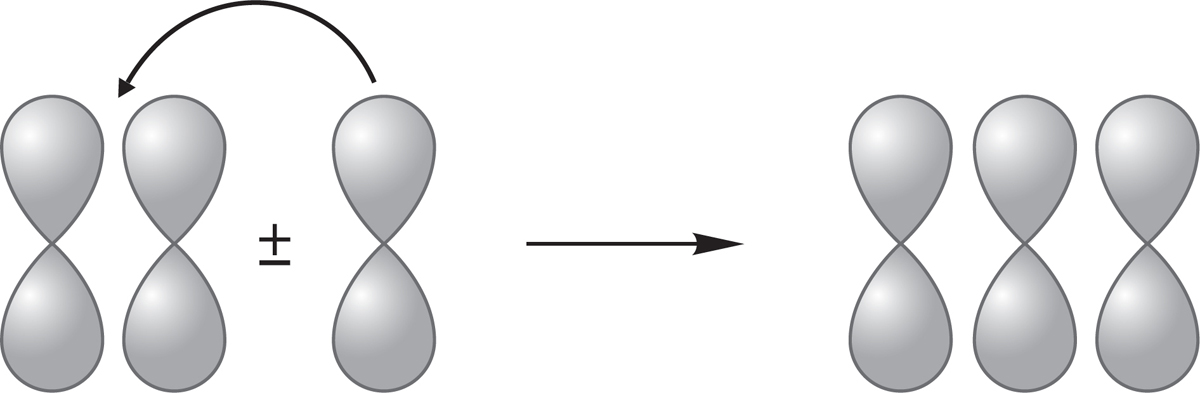
PROBLEM 1.66 One can generate the molecular orbitals for triangular H3 simply by bending the orbitals generated in Problem 1.64 to transform the linear molecule into the bent one.
(a) Bend the three molecular orbitals for HHH to make the orbitals for the triangle. Make careful drawings. Note that as the old H(1) and H(3) come closer together in the triangle, they will create a new bonding or antibonding interaction.
(b) Order the new molecular orbitals in energy by counting the nodes.
(c) Which will be lower in energy, linear or triangular H3+? What a sophisticated question! Yet, given the answer to Problems 1.64 and 1.65, it is easy.
PROBLEM 1.67 In the chapter, we made the two molecular orbitals for H2 (p. 35), and in Problem 1.64 we used the two molecular orbitals of H2 and a 1s orbital to make HHH. This time, generate the molecular orbitals for HHHH, linear H4, from the molecular orbitals of two H2 molecules placed end to end. Remember: At this level of “theory,” you need only interact orbitals closest in energy.

Order the new molecular orbitals in energy by counting the nodes, and place the proper number of electrons in the orbitals.
PROBLEM 1.68 Make the molecular orbitals for square H4 by allowing the molecular orbitals of H2 to interact as shown below:
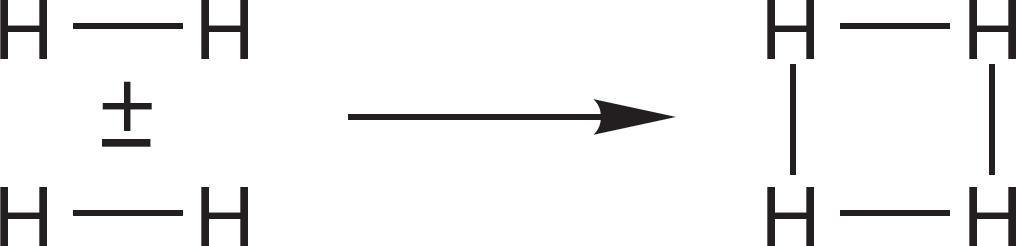
Order the new molecular orbitals by counting the nodes, and add the proper number of electrons. You might check your answer by deriving the same orbitals. Do this by bending the molecular orbitals for linear HHHH developed in Problem 1.67.
Use Organic Reaction Animations (ORA) to answer the following questions:
PROBLEM 1.69 Choose the reaction titled “Unimolecular nucleophilic substitution” and click on the Play button. Do you suppose the first step of this reaction is a homolytic or a heterolytic cleavage? Observe the Highest Occupied Molecular Orbital (HOMO) track by clicking on the HOMO button. The location (orbital) of the most available electrons will be shown throughout the reaction. Notice that the electron density goes with the bromine as it comes off. That should help you answer this question.
PROBLEM 1.70 Choose the “Introduction” on the bottom left of the Table of Contents page. Read this short document. Under the “Technical Issues” heading there is a discussion of solvent effects. After reading this section, how do you think use of a polar solvent in the “Unimolecular nucleophilic substitution” reaction might affect the answer to the previous question? That is, would a polar solvent have more impact on a homolytic or a heterolytic cleavage?
PROBLEM 1.71 Choose the reaction “Alkene hydrohalogenation” and observe the molecule that initially comes to the screen. It has a carbon–carbon double bond. Click on the HOMO button. Observe the calculated area for the π bond that is shown to answer the following questions. Is the electron density of a π bond constrained to the space between the carbons? Do you suppose the π bond electrons are held more or less tightly than σ bond electrons?
If your instructor assigns problems in  , log in at smartwork.wwnorton.com.
, log in at smartwork.wwnorton.com.
 C
C