2.5 Ethane (C2H6), Ethyl Compounds (C2H5X), and Newman Projections
There is a special substituent X that produces a most interesting H3C―X. In this case, we let X = CH3, another methyl group. Now H3C―X becomes H3C―CH3, which can also be written as C2H6. This molecule is ethane (Fig. 2.19), the second member of the alkane family. You might try to anticipate the following discussion by building a model of ethane and examining its structure now.
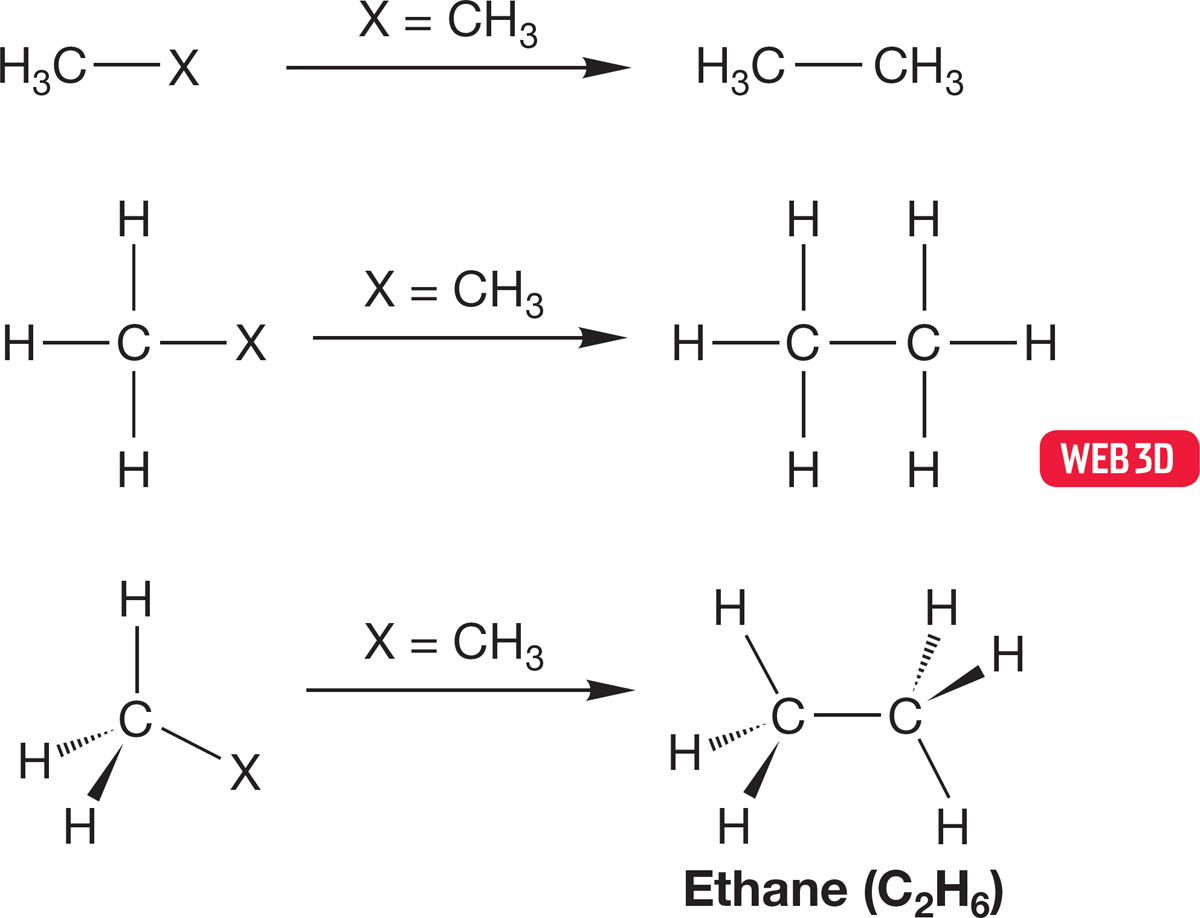
FIGURE 2.19 The construction of ethane (H3C—CH3) by the replacement of X in H3C—X with a methyl group.
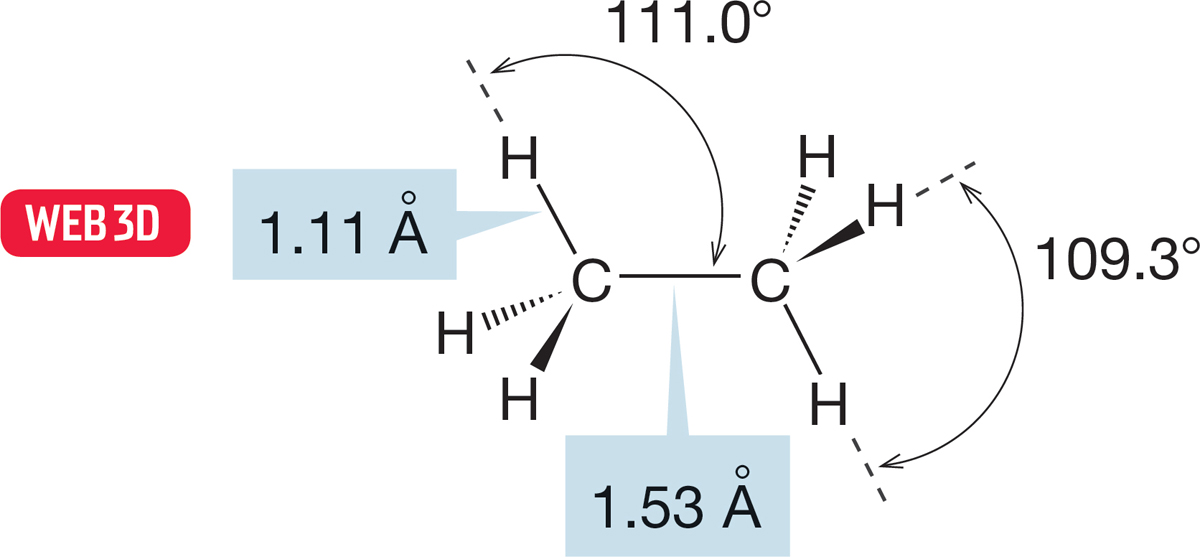
FIGURE 2.20 The detailed structure of ethane.
Even in a molecule as simple as ethane, several interesting structural questions arise. From the point of view of one carbon, the attached methyl group takes up more room than the much smaller hydrogens. So we expect the H3C―C―H angle to be slightly larger than the H―C―H angle, and that is the case: H―C―CH3 = 111.0° and H―C―H = 109.3° (Fig. 2.20).
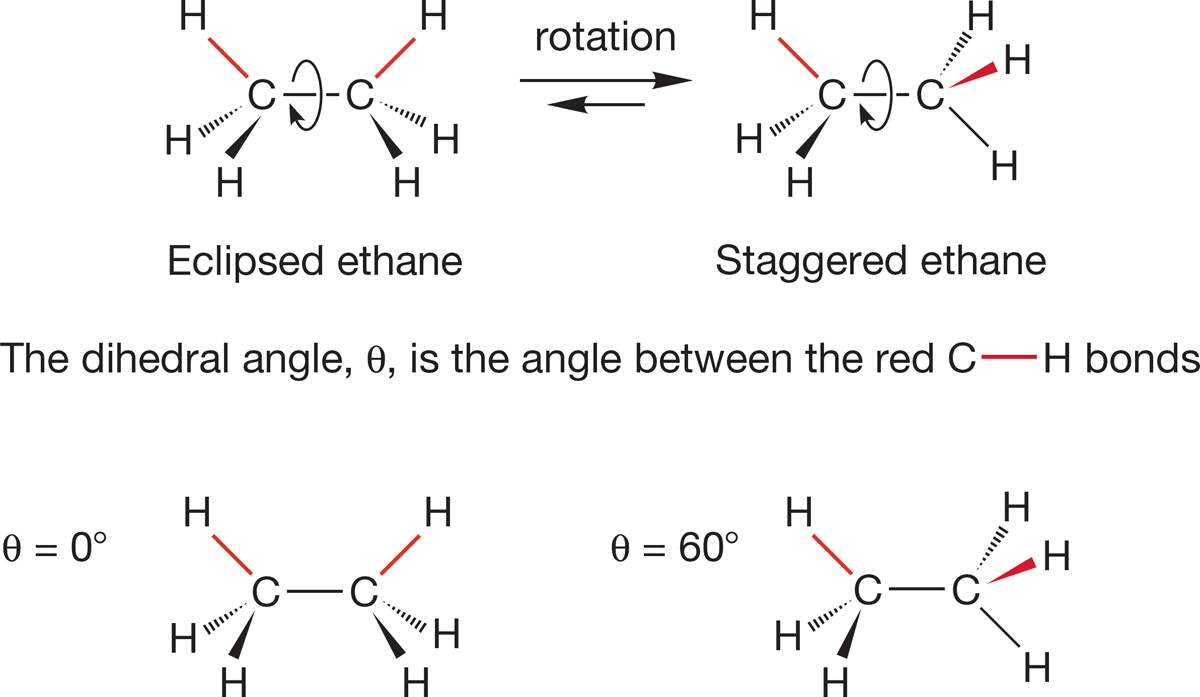
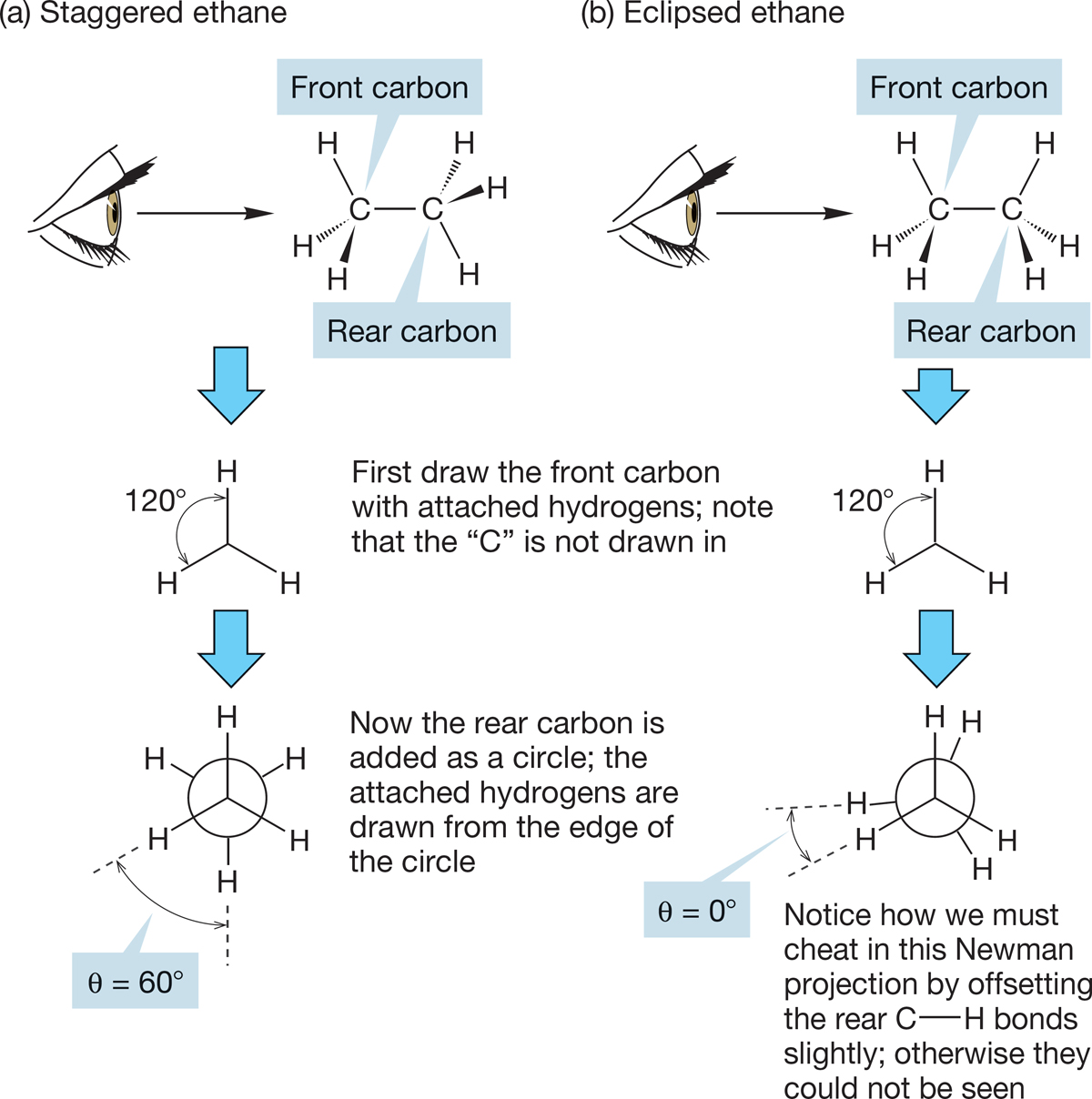
FIGURE 2.21 Two conformations of ethane: the eclipsed and staggered forms.
How are the hydrogens of one end of the ethane molecule arranged with respect to the hydrogens at the other end? There are two important structures for ethane, which are related by rotation about the C―C bond. Molecules that differ in spatial orientation as a result of rotation around a sigma bond are called conformers. The two important conformations for ethane are eclipsed ethane and staggered ethane, each shown in a side view in Figure 2.21. If you look down the C―C bond (Fig. 2.21), you can see that in the eclipsed conformation, each of the three hydrogens on the front methyl eclipses a hydrogen on the back methyl. In the staggered conformation, the view down the C―C bond shows the hydrogens in front arranged so that each hydrogen in back can be seen. When we look down the C―C bond in this way, the angle between a hydrogen in front and a hydrogen in back is called the dihedral angle. The dihedral angle is measured in degrees θ (pronounced thā-ta). The dihedral angle between the hydrogens in the eclipsed ethane is 0°. The dihedral angle in the staggered conformation is 60°. Ethane can exist in an infinite number of conformations, depending on the value of the dihedral angle. We focus here on the two extreme structures, eclipsed and staggered ethane. Be sure you see how these two forms are interconverted by rotation about the carbon–carbon bond. Use a model!
Newman projections are extraordinarily useful in making three-dimensional structures clear on a two-dimensional surface. For example, Figure 2.22a makes it obvious that all six hydrogens in staggered ethane are the same—they are equivalent in the language of organic chemistry.
PROBLEM 2.12 Draw Newman projections for the staggered conformations of ethyl chloride (CH3―CH2―Cl) and 1,2-dichloroethane (Cl―CH2―CH2―Cl). In the second case, there are two staggered conformations of different energy. Can you estimate which is more stable?
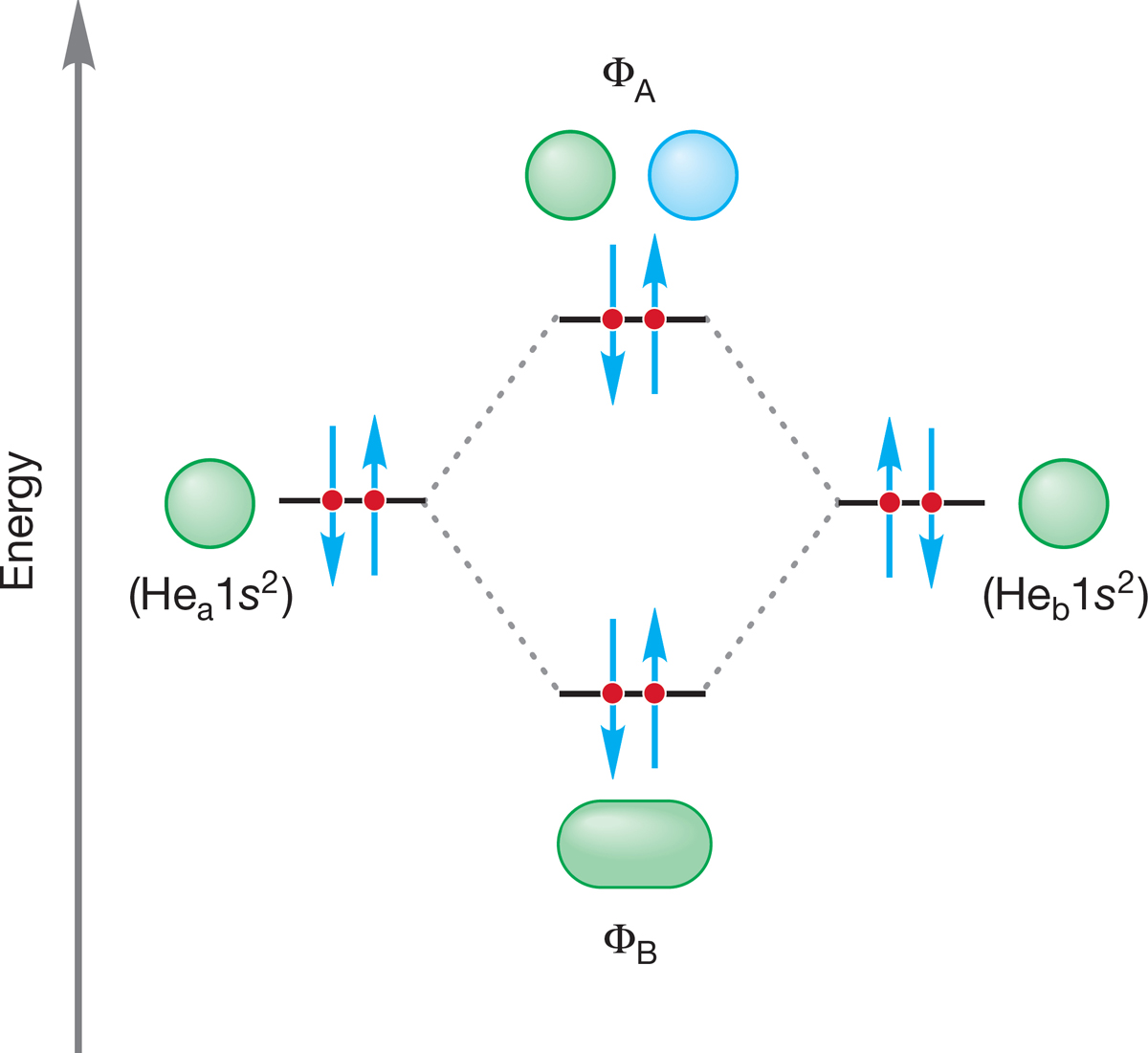
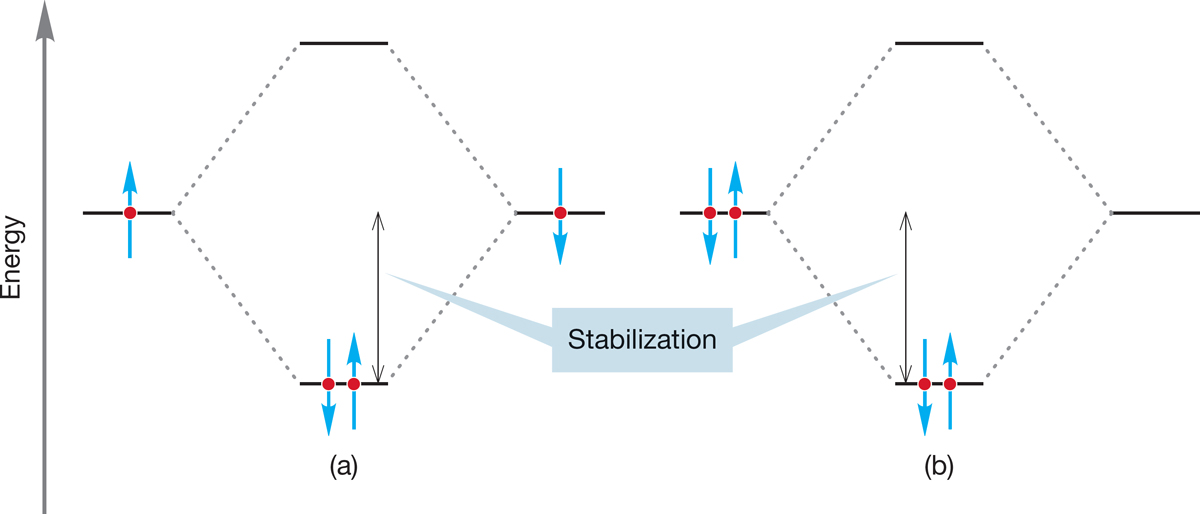
Which of the two limiting conformations of ethane represents the more stable molecule? We would surely guess that it would be the staggered conformation, and that guess would be exactly right. But the reason has little to do with the “obvious” spatial requirement for the hydrogens. The hydrogens do not compete for the same space in the eclipsed conformation. There may be some electrostatic repulsion between the electrons in the bonds that are eclipsed, but the eclipsed conformation is mostly destabilized by the repulsive interaction of two filled orbitals in each of the three pairs of eclipsed carbon–hydrogen bonds (Fig. 2.22b).
WORKED PROBLEM 2.13 Use an orbital interaction diagram like the one for He2 in Figure 1.48 (p. 42) to show the destabilization in eclipsed ethane. How many eclipsing filled orbital–filled orbital interactions are present?
ANSWER In eclipsed ethane, there are three instances in which two filled carbon–hydrogen orbitals overlap. The figure shows one of them.
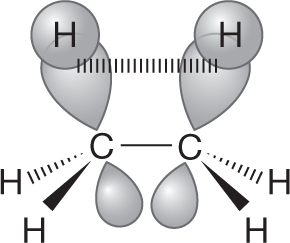
Here is the orbital interaction diagram. Notice that the new antibonding orbital, σ − σ, is filled.
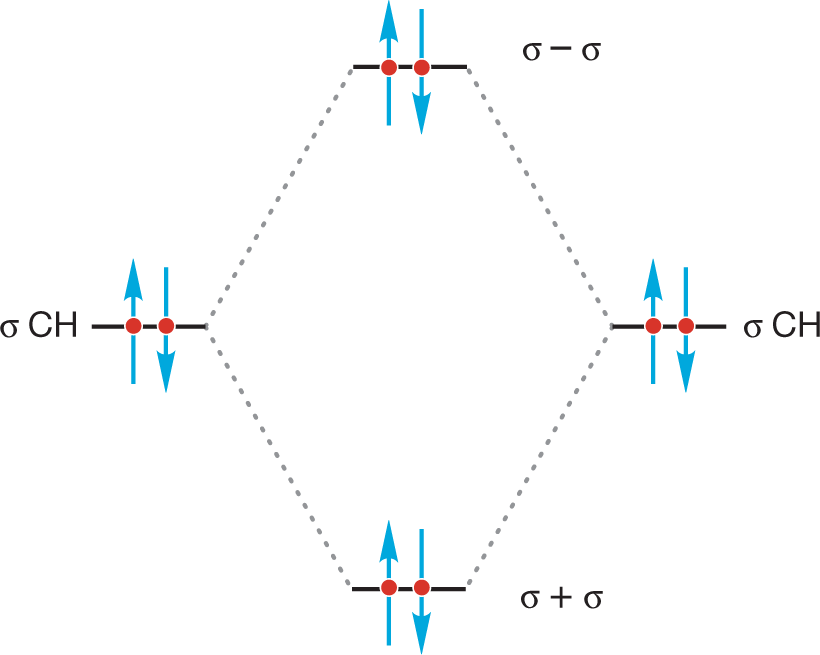
PROBLEM 2.14 There is a related orbital effect that stabilizes staggered ethane. Use an orbital interaction diagram like the one for H2 in Figure 1.49b (p. 44) to show the stabilization in staggered ethane. This problem is much harder than Problem 2.13, so here is some help in the form of a set of tasks. The explanation that this problem leads to was first pointed out to MJ by an undergraduate just like you about 30 years ago.
(a) Draw staggered ethane in a Newman projection.
(b) Draw the antibonding orbital for one of the C―H bonds of the front carbon.
(c) Consider the C―H bond that is directly behind the antibonding orbital you have drawn. Can you see the overlap between the filled bonding orbital in back and the empty antibonding orbital you drew?
(d) What factor stabilizes the staggered conformation of ethane over the eclipsed conformation? How many interactions in the staggered conformation of ethane have overlap of bonding and antibonding orbitals?
If you can fight your way through this problem, you are in excellent shape in terms of manipulation of orbitals!
We can now make a plot of dihedral angle as a function of energy (Fig. 2.23). Calculations show that the eclipsed form of ethane is an energy maximum, the top of the energy barrier separating two staggered forms. Such a maximum-energy point is called a transition state (TS).
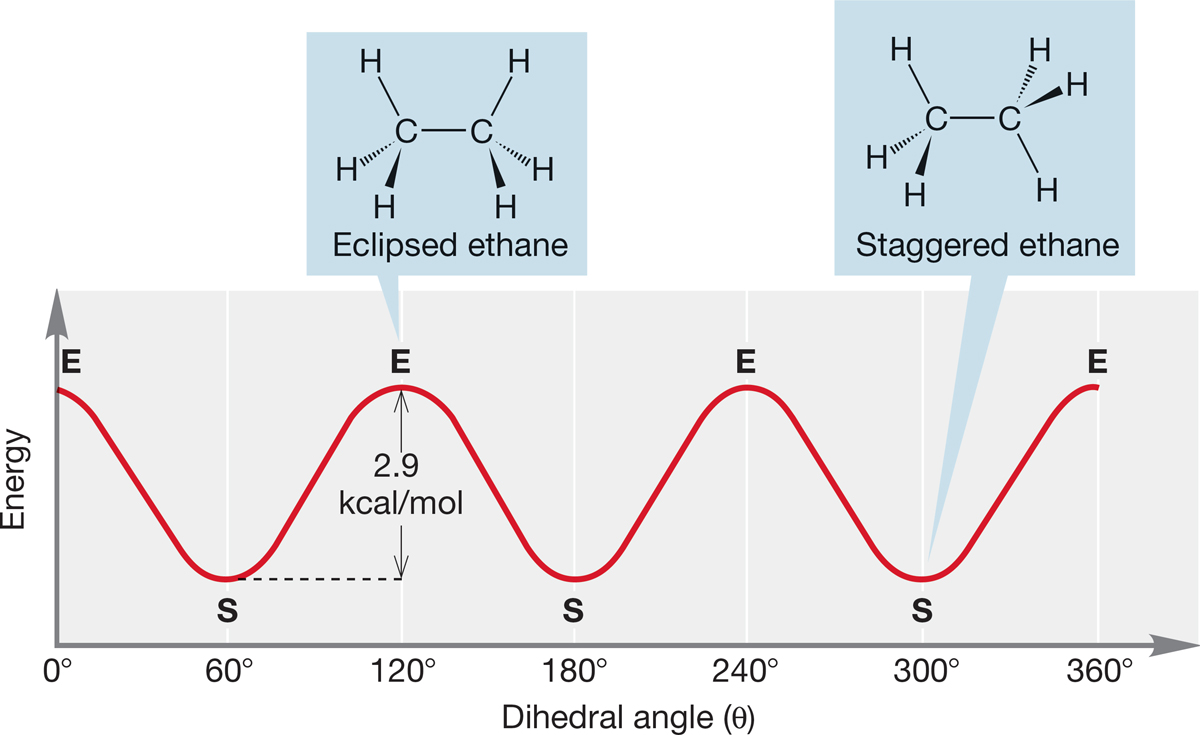
FIGURE 2.23 A plot of the energy of ethane as rotation around the carbon–carbon bond occurs (E = eclipsed, S = staggered).
PROBLEM 2.15 You recently saw a transition state, although the term wasn’t used. Where? Hint: Where have we described two forms of a molecule that interconvert by passing through another species? It is close by.
How big is the energy difference between the staggered and eclipsed conformations of ethane? This question asks how high the energy barrier is between two of the minimum-energy staggered forms in Figure 2.23. The barrier turns out to be a small number, 2.9 kcal/mol (12.1 kJ/mol), an amount of energy easily available at room temperature. At normal ambient temperatures, ethane is said to be freely rotating because there is ample thermal energy to traverse the barrier separating any two staggered forms. On some very cold planet, however, where there would be much less thermal energy available than on Earth, alien organic chemists would have to worry more about this rotational barrier. Thus, their lives would be even more complicated than ours.
PROBLEM 2.16 Draw the low-energy Newman projection for the structure depicted below by looking down the carbon–carbon bond.
PROBLEM 2.17 Imagine 1,2-dideuterioethane (DCH2—CH2D), where D = deuterium, on some cold place such as Pluto. If there were not enough energy available to overcome the barrier to rotation, how many 1,2-dideuterioethanes would there be?
The chemical and physical properties of ethane closely resemble those of methane. Both are gases at room temperature, and both are quite unreactive under most chemical conditions—but not all conditions! You need only light a match in a room containing either ethane or methane and air to find that out. This reaction is actually very interesting. If we examine the debris after the explosion, we find two new molecules, water and carbon dioxide:
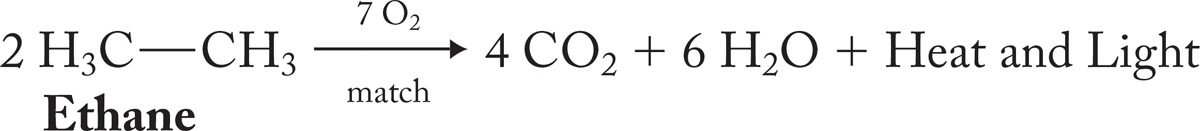
A thermochemical analysis indicates that water and carbon dioxide are more stable than ethane and oxygen. Presumably, this is the reason ethane explodes when the match is lit. Energy is all too obviously given off as heat and light. But why do objects that are stable in air, such as ethane or wood, explode or burn continuously when ignited? How are they protected until the match is lit?
We’ll approach these questions in later chapters, but it’s worth some thought now in anticipation. This matter is serious because the molecules in our bodies are also less thermodynamically stable than their various oxidized forms, and we live in an atmosphere that contains about 20% oxygen. Why can humans live in such an atmosphere without spontaneously bursting into flame? This issue has been of some concern, and not only for scientists.4
We can imagine making ethane by allowing two methyl radicals to come together (Fig. 2.24). The two sp3 hybrid orbitals, one on each carbon, overlap to form a new carbon–carbon bond. This orbital overlap produces a bonding molecular orbital, which is a σ orbital because of its cylindrical symmetry. You will recall that the process simultaneously creates an antibonding molecular orbital (σ*). The bonding orbital is filled by the two electrons originally in the two methyl radicals, and the antibonding orbital is empty. We might guess that the overlap of the two equal-energy sp3 hybrid orbitals would be very favorable, and it is. The carbon–carbon bond in ethane has a strength of about 90 kcal/mol (377 kJ/mol). This value is the amount of energy by which ethane is stabilized relative to a pair of separated methyl radicals and is therefore the amount of energy required to break this strong carbon–carbon bond. The formation of ethane from two methyl radicals is exothermic by 90 kcal/mol:
H3C· + ·CH3 ➔ H3C―CH3 ΔH° = −90 kcal∙mol
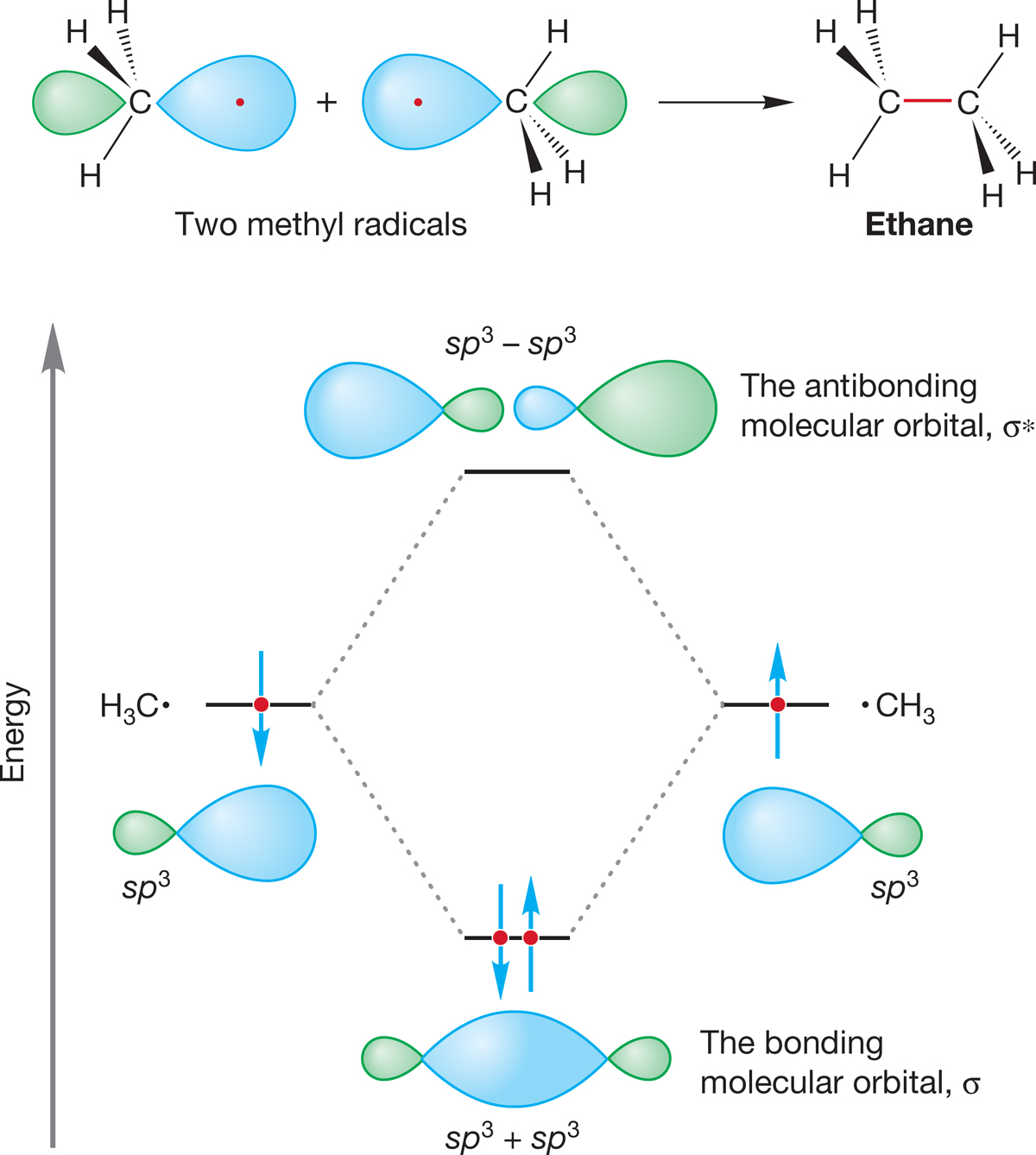
FIGURE 2.24 An orbital interaction diagram for the formation of ethane through the combination of a pair of methyl radicals.
and the dissociation of ethane into two methyl radicals is endothermic by 90 kcal/mol:
H3C — CH3 ➔ H3C· + ·CH3 ΔH° = +90 kcal∙mol
Thus, the carbon–carbon bond dissociation energy of ethane is this same 90 kcal/mol. For a summary of bond dissociation energies, see Table 1.10 (p. 40).
Just as we imagined replacing one of the hydrogens in methane with an X group to generate the series of methyl compounds, so we can produce ethyl compounds (CH3CH2―X) from ethane. Indeed, we can now generalize: Substituted alkanes are called alkyl compounds, often abbreviated R―X, where R stands for a generic alkyl group. Table 2.3 shows some common ethyl compounds and a few of their physical properties.
TABLE 2.3 Some Simple Derivatives of Ethane: Ethyl Compounds
CH3CH2―X |
Common Name |
mp (°C) |
bp (°C) |
Physical Properties |
CH3CH2―H |
Ethane |
−183.3 |
−88.6 |
Colorless gas |
CH3CH2―OH |
Ethyl alcohol, or ethanol |
−117.3 |
78.5 |
Colorless liquid |
CH3CH2―NH2 |
Ethylamine |
−81 |
16.6 |
Colorless gas/liquid |
CH3CH2―Br |
Ethyl bromide |
−118.6 |
38.4 |
Colorless liquid |
CH3CH2―Cl |
Ethyl chloride |
−136.4 |
12.3 |
Colorless gas/liquid |
CH3CH2―CN |
Ethyl cyanide, or propionitrile |
−92.9 |
97.4 |
Colorless liquid |
CH3CH2―F |
Ethyl fluoride |
−143.2 |
−37.7 |
Colorless gas |
CH3CH2―I |
Ethyl iodide |
−108 |
72.3 |
Colorless liquid |
CH3CH2―SH |
Ethanethiol, or ethyl mercaptan |
−144 |
35 |
Colorless liquid |
+CH2CH3 |
Ethyl cation (reactive intermediate) |
|||
-:CH2CH3 |
Ethyl anion (reactive intermediate) |
|||
·CH2CH3 |
Ethyl radical (reactive intermediate) |
|||
mp, melting point; bp, boiling point.
How many different CH3CH2―X compounds are there? From a two-dimensional representation of ethane (Fig. 2.25a), there appear to be two ethyl compounds with the same formula but different structures. Compounds of this type, which have the same molecular formula but are not the same structure, are called isomers (from the Greek words meaning “the same parts”). If the two ethyl compounds of Figure 2.25a existed, they would be isomers of each other. However, the two different positions shown for X (at the “top” of the molecule and on the “side”) do not in fact exist. They are artifacts of our attempt to represent a three-dimensional molecule in two dimensions. This common student misconception demonstrates how important it is to know the three-dimensional structures of compounds. As we can see in Figure 2.22a, all six hydrogens in ethane are equivalent, and therefore there is only one kind of substituted ethyl compound (Fig. 2.25b). Different conformations of a substituted ethyl compound do exist. We know about the staggered and eclipsed conformations, and we can call these conformational isomers because the two conformations have the same molecular formula and are made up of the same molecular parts (methyl groups, functional groups, etc.) but differ as a result of rotation around a sigma bond. However, even though most conformational isomers have relatively low barriers to rotation, we usually focus on the most stable representation. In the ethyl series, we will work with the staggered structure.
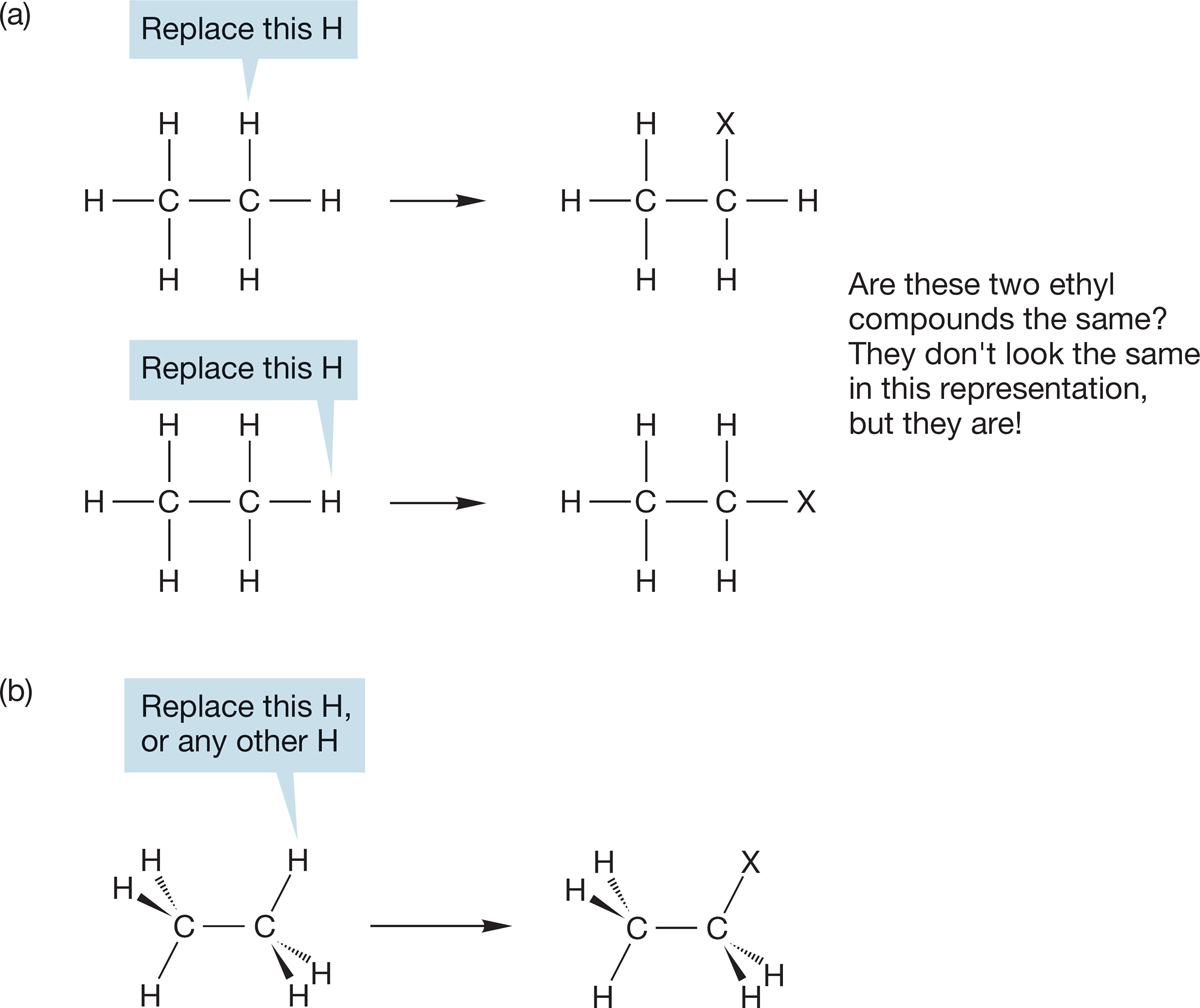
FIGURE 2.25 (a) A two-dimensional representation of ethane suggests that there are two different kinds of ethyl compound, CH3CH2―X. (b) We must look at ethane in three dimensions to see why there is only one CH3CH2―X.
Summary
Even a molecule as simple as ethane, the two-carbon alkane, has a complex structure. For example, staggered and eclipsed conformational isomers exist, separated by a low barrier to rotation (∼ kcal/mol). Because this barrier is so low, rapid rotation occurs around the carbon–carbon bond. All six hydrogens in ethane are equivalent; there is only one ethane and only one kind of ethyl derivative. You may need a ball-and-stick model set to convince yourself.
4Eliot . . . claimed to be deeply touched by the idea of an inhabited planet with an atmosphere that was eager to combine violently with almost everything the inhabitants held dear . . . “When you think of it, boys,” he said brokenly, “that’s what holds us together more than anything else, except maybe gravity. We few, we happy few, we band of brothers—joined in the serious business of keeping our food, shelter, clothing and loved ones from combining with oxygen.”
—Kurt Vonnegut
God Bless You, Mr. Rosewater
 C
C C
C